Презентация на тему: линейные дифференциальные уравнения первого порядка

Тема урока: Линейные дифференциальные уравнения первого порядка Преподаватель математики и физики ГБПОУ Салаватского индустриального колледжа Ягаффарова Д.У. 2015г.

Опрос 1. Какое уравнение называется дифференциальным? Уравнение, содержащее производные искомой функции или её дифференциалы. 3.Что значит решить ДУ? Найти такую функцию, подстановка которой в это уравнение обращает его в тождество. 4. Какое решение ДУ называется общим? Решение, содержащее произвольную постоянную С. 5. Какое решение ДУ называется частным? Решение, в которое подставлено числовое значение С. 2. Какие из следующих уравнений являются дифференциальными?

Опрос 7. Определите порядок следующих ДУ: 9. Какое уравнение называется ДУ первого порядка с разделяющимися переменными? Уравнение вида Уравнение вида 8. Какое уравнение называется ДУ первого порядка с разделёнными переменными? 6. Что называется порядком ДУ? Наивысший порядок производной, входящий в уравнение.

Линейные дифференциальные уравнения первого порядка Иоганн Бернулли (1667—1748) Яков Бернулли (1654-1705) К портрету Иоганна Вольтер написал четверостишие: Его ум видел истину, Его сердце познало справедливость. Он — гордость Швейцарии И всего человечества.

Объекты, названные в честь членов семьи Дифференциальное уравнение Бернулли — в честь Якова. Закон Бернулли и Интеграл Бернулли в гидродинамике — в честь Даниила. Лемниската Бернулли — в честь Якова. Многочлен Бернулли — в честь Якова. Неравенство Бернулли — в честь Иоганна. Распределение Бернулли в теории вероятностей — в честь Якова. Числа Бернулли — в честь Якова. Три поколения Бернулли дали 8 крупных математиков и физиков. Среди академиков Петербургской Академии наук — пятеро представителей семьи Бернулли. В честь Якова и Иоганна Бернулли назван кратер на Луне.

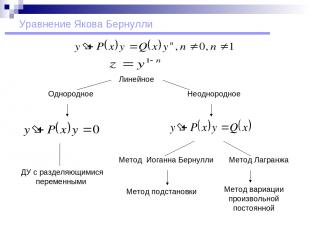
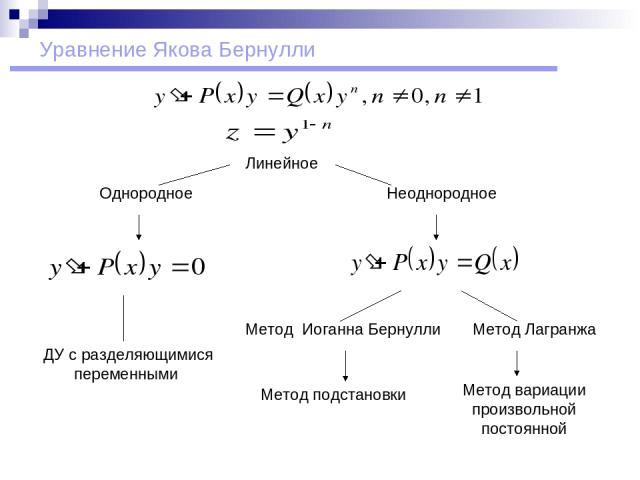
Уравнение Якова Бернулли Метод Лагранжа ДУ с разделяющимися переменными Неоднородное Однородное Метод Иоганна Бернулли Метод вариации произвольной постоянной Метод подстановки Линейное

Линейные дифференциальные уравнения первого порядка Линейное ДУ первого порядка называется однородным, если функция Замечание. Уравнение называется линейным, так как искомая функция y и её производная y’ входят в это уравнение в первой степени. Уравнение вида , где и – функции переменной или постоянные величины, называется линейным дифференциальным уравнением первого порядка Линейное ДУ первого порядка называется неоднородным, если функция

1) Какие из данных уравнений являются линейными уравнениями первого порядка, а какие нет и почему? 1) Есть линейное уравнение первого порядка, так как y и y’ входят в первой степени, а - функции одной переменной х 2) 3) 2) Не является линейным, так как содержит вторую производную 3) Не является линейным, так как содержит

Линейное однородное ДУ первого порядка 1. Решить уравнение Решение: имеем Получаем (общее решение) 2. Решить уравнение Выразить производную функции через дифференциалы Разделить переменные Интегрировать (общее решение) Решение:

Линейное неоднородное ДУ. Метод Иоганна Бернулли Замечание. Любую величину можно представить в форме произведения двух сомножителей, причем один из множителей можно выбрать по своему желанию. В результате линейное неоднородное ДУ сводиться к двум уравнениям с разделяющимися переменными: где и - новые функции переменной 1. Решить уравнение Решение: Положим тогда или

Получим или Выразить производную функции через дифференциалы Разделить переменные Интегрировать С=0, ввиду произвольности в выборе (1) Имеем

Выразить производную функции через дифференциалы Разделить переменные Интегрировать постоянную С писать обязательно Окончательно получим (общее решение) Замечание. Уравнение (1) можно было записать в эквивалентном виде:

Алгоритм решения линейного ДУ первого порядка 1. Приводят уравнение к виду находят 2. Используя подстановку и подставляют эти выражения в уравнение. 3. Группируют члены уравнения, выносят одну из функций за скобки. Находят вторую функцию, приравняв выражение в скобках нулю и решив полученное уравнение. 4. Подставляют найденную функцию в оставшееся выражение и находят вторую функцию. 5. Записывают общее решение, подставив выражения для найденных функций и в равенство 6. Если требуется найти частное решение , то определяют С из начальных условий и подставляют в общее решение. или

Примеры Решить уравнения: 1. 2. Ответ: Ответ:

Вопросы для самоконтроля: 1. Какое уравнение называется линейным ДУ первого порядка? 2. При каких условиях линейное ДУ первого порядка называется однородным? ДУ с разделяющимися переменными 3. К какому ДУ приводится линейное однородное уравнение ? 4. Какими методами решается линейное неоднородное ДУ ? Методы Бернулли, Лагранжа 5. В чем заключается метод Бернулли? В подстановке

Домашнее задание 1. Решить линейное ДУ первого порядка 2. Решить задачу Коши для линейного ДУ первого порядка

Спасибо за внимание