Презентация на тему: Логические основы компьютера Базовые логические элементы

Логические основы компьютера Базовые логические элементы Автор: Сергеев Евгений Викторович МОУ СОШ №4 г. Миньяра Челябинской области [email protected] http://shk4-minyar.ucoz.ru

Базовые логические элементы Компьютер выполняет арифметические и логические операции при помощи т.н. базовых логических элементов, которые также еще называют вентилями. Вентиль «И» – конъюнктор. Реализует конъюнкцию. Вентиль «ИЛИ» – дизъюнктор. Реализует дизъюнкцию. Вентиль «НЕ» – инвертор. Реализует инверсию

Составные элементы Любая логическая операция может быть представлена через конъюнкцию, дизъюнкцию и инверсию Любой сколь угодно сложный элемент компьютера может быть сконструирован из элементарных вентилей

Сигналы-аргументы и сигналы-функции Вентили оперируют с электрическими импульсами: Импульс имеется – логический смысл сигнала «1» Импульса нет – логический смысл сигнала «0» На входы вентиля подаются импульсы – значения аргументов, на выходе вентиля появляется сигнал – значение функции

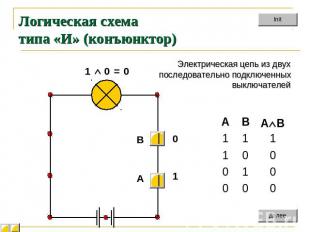
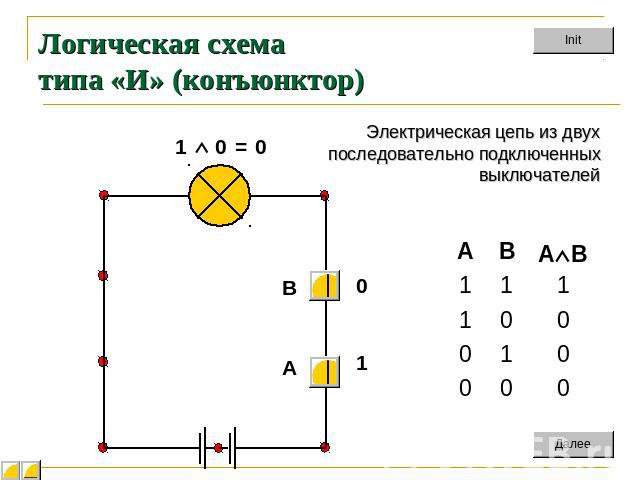
Логическая схема типа «И» (конъюнктор) Электрическая цепь из двух последовательно подключенныхвыключателей

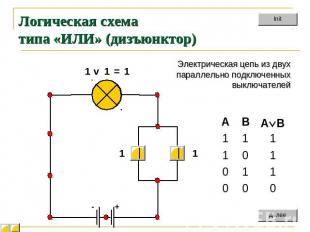
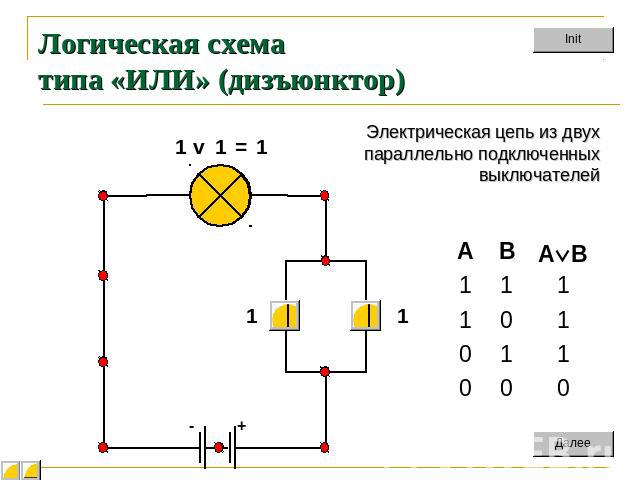
Логическая схема типа «ИЛИ» (дизъюнктор) Электрическая цепь из двух параллельно подключенныхвыключателей

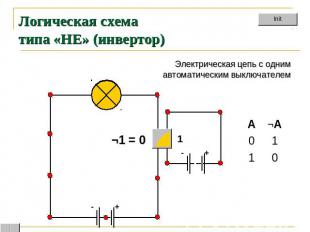
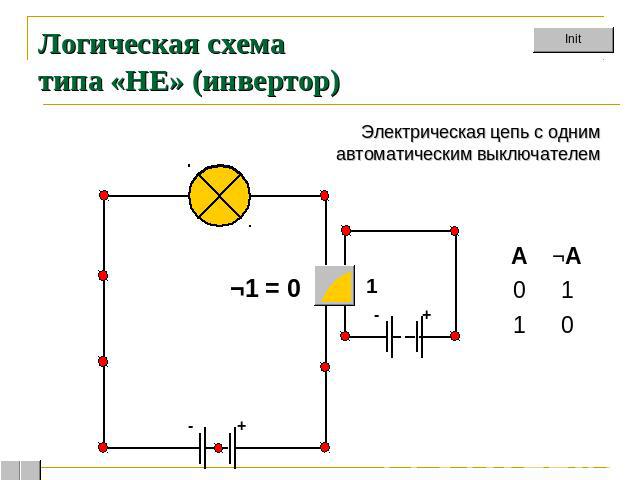
Логическая схема типа «НЕ» (инвертор) Электрическая цепь с однимавтоматическим выключателем

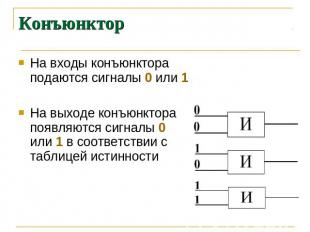
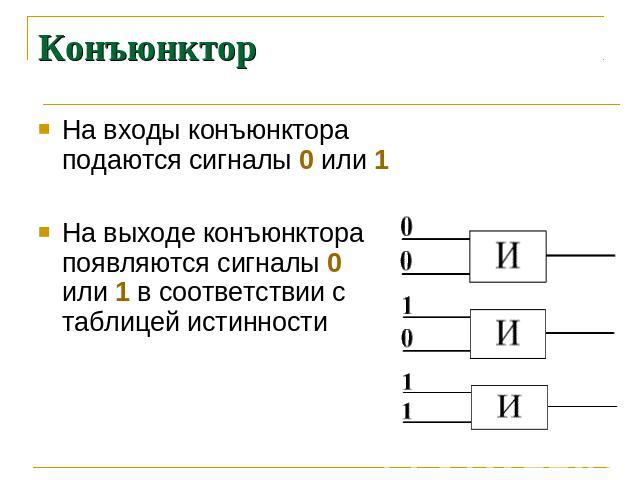
Конъюнктор На входы конъюнктора подаются сигналы 0 или 1 На выходе конъюнктора появляются сигналы 0 или 1 в соответствии с таблицей истинности

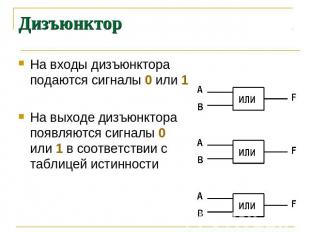
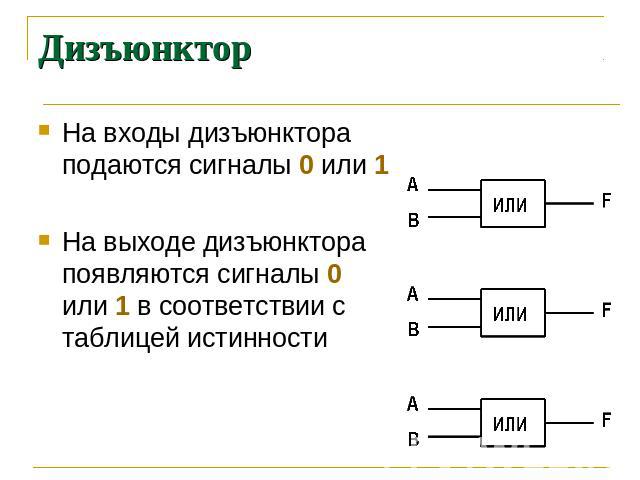
Дизъюнктор На входы дизъюнктора подаются сигналы 0 или 1 На выходе дизъюнктора появляются сигналы 0 или 1 в соответствии с таблицей истинности

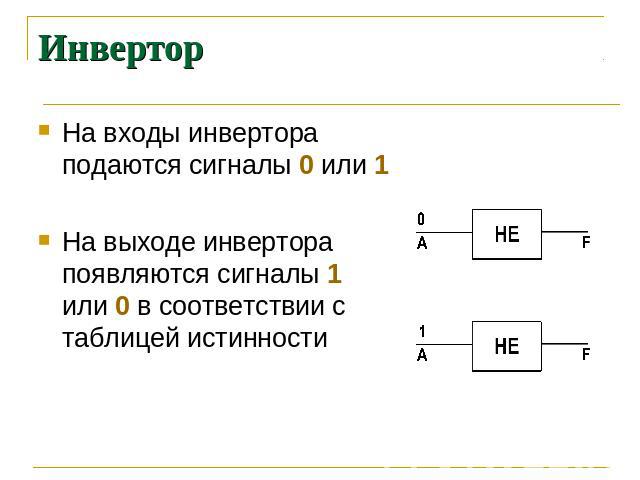
Инвеpтор На входы инвертора подаются сигналы 0 или 1 На выходе инвертора появляются сигналы 1 или 0 в соответствии с таблицей истинности

Сумматор двоичных чисел Любое математическое сколь угодно сложное выражение может быть представлено в виде последовательности элементарных математических операций Все математические действия в компьютере сводятся к сложению двоичных чисел Основу микропроцессора составляют сумматоры двоичных чисел

Полусумматор. Арифметическое сложение двоичных чисел В каждом разряде образуется сумма цифр в соответствующих разрядах слагаемых, при этом возможен перенос единицы в старший разряд

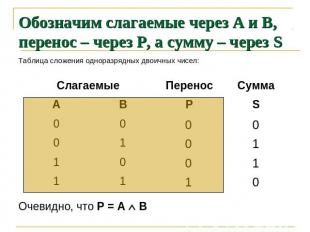
Обозначим слагаемые через А и В, перенос – через Р, а сумму – через S Таблица сложения одноразрядных двоичных чисел:

Получаем формулу для вычисления S Если сравнить АВ c S:

Получаем формулу для вычисления S S = (А В) ¬P (А В) ¬(A B)

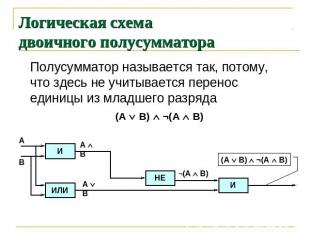
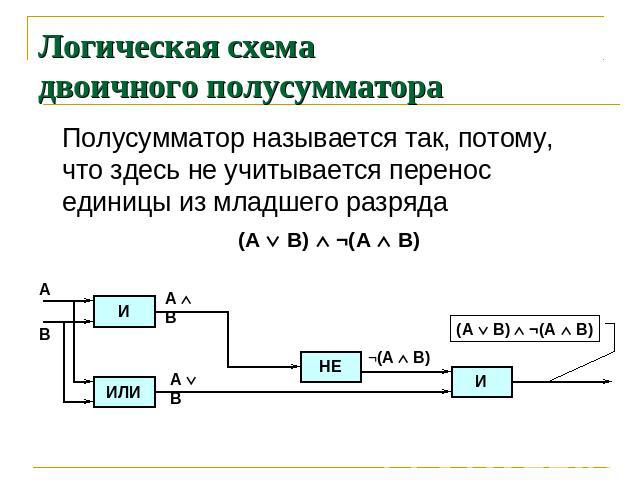
Логическая схема двоичного полусумматора Полусумматор называется так, потому, что здесь не учитывается перенос единицы из младшего разряда

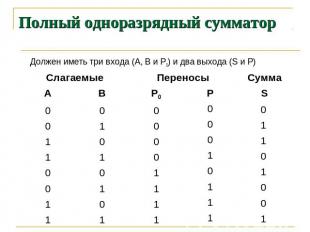
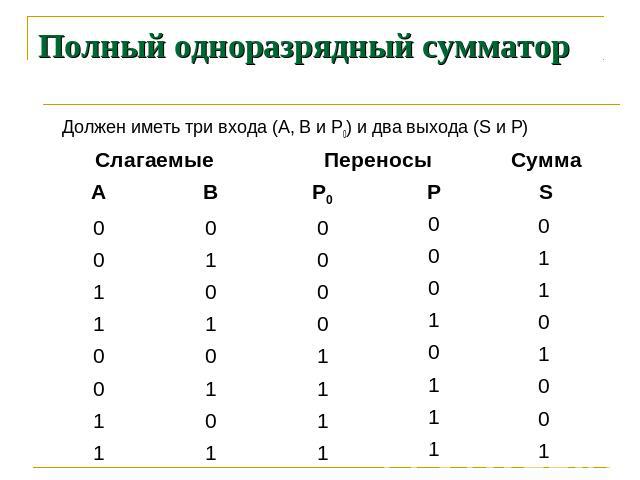
Полный одноразрядный сумматор Должен иметь три входа (А, В и Р0) и два выхода (S и P)

Формула полного одноразрядного сумматора Р принимает значение 1 когда хотя бы две из трех переменных равны 1: Р = (А B) (A P0) (B P0) Сумма равна произведению логического сложения (А, В и Р0) на инвертированный перенос ¬Р: S = (А В Р0) ¬Р Это выражение справедливо во всех случаях, кроме одного, когда А, В и Р0 равны 1:

Формула полного одноразрядного сумматора Правильное значение суммы – 1. Для ее получения необходимо полученное выражение сложить с произведением этих же переменных: S = (А В Р0) ¬Р (А В Р0)

Многоразрядный сумматор Построен на основе полных одноразрядных сумматоров (по одному на каждый разряд), причем таким образом, чтобы выход (перенос) младшего сумматора был подключен ко входу старшего сумматора

Триггер Важнейшая структурная единица оперативной памяти и регистров процессора Состоит из двух логических элементов «ИЛИ» и двух логических элементов «НЕ»

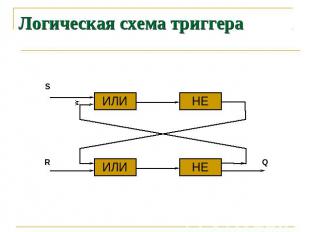
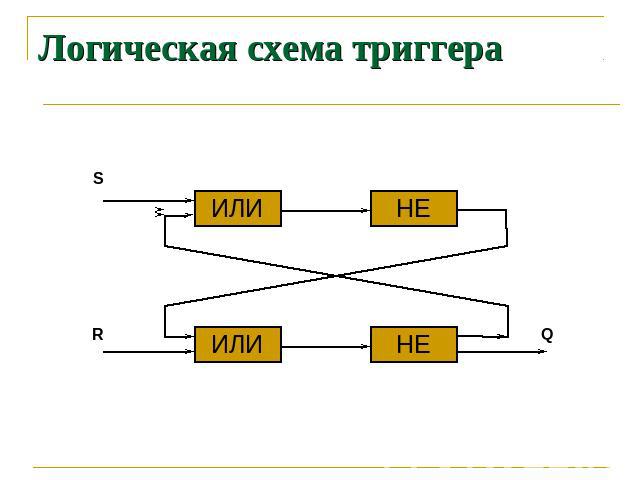
Логическая схема триггера

Работа триггера В обычном состоянии на входы триггера S и R подан сигнал «0» и триггер хранит «0». При подаче сигнала «1» на вход S триггер принимает значение на выходе Q значение «1» При подаче сигнала «1» на вход R триггер возвращается в свое исходное состояние – хранит «0»