Презентация на тему: Тригонометрические уравнения. Арксинус

Тригонометрические уравнения. Арксинус

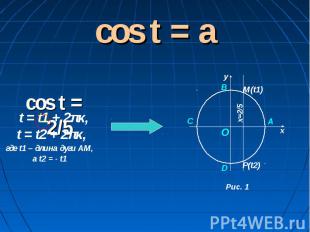
cos t = acos t = 2/5t = t2 + 2πκ, где t1 – длина дуги АМ, а t2 = - t1

t1 є [ 0; π/2 ] t1 = arccos 2/5 t2 = - arccos 2/5 arccos 2/5

cos t = 2/5 t = arccos 2/5 + 2πκ t = - arccos 2/5 + 2πκ t = ±arccos 2/5 + 2πκ

Что же такое arccos 2/5? Это число (длина дуги АМ), косинус которого равен 2/5 и которое принадлежит отрезку [ 0; π/2 ].

cos t = a cos t = - 2/5 t = t2 + 2πκ, где t1 – длина дуги АМ, а t2 = - t1 t = arccos (-2/5) + 2πκ t = - arccos (-2/5) + 2πκ t = ±arccos 2/5 + 2πκ

Что же такое arccos (-2/5)? Это число (длина дуги АМ), косинус которого равен -2/5 и которое принадлежит отрезку [ π/2; π].

Определение Если |а|≤1, то arccos a (арккосинус а) – это такое число из отрезка [ 0; π], косинус которого равен а. Если |а|≤1, тоarccos a = t cos t =a,0 ≤ t ≤ π.

Общий вывод о решении уравнения cos t =a Если |а|≤1, то уравнение cos t = a имеет решения t = ±arccos a + 2πκ, k є Z

Пример Вычислить: arccos ½Решение:Пусть arccos ½ = t. Тогда cos t = ½ и t є [ 0; π]. Значит, t = π/3, поскольку cos π/3 = ½ и π/3 є [ 0; π]. Итак, arccos ½ = π/3.

ТеоремаДля любого а є [-1;1] выполняется равенство arccos a + arccos (-a) = π. arccos a + arccos (-a) = AM + AP = PC +AP = AC = π

Спасибо за внимание!