Презентация на тему: Неполные квадратные уравнения

Урок по теме \"Неполные квадратные уравнения\". Подготовили учителя математики МОУ \"Успенская ООШ МО \"Ахтубинский район\" Зенина Н.Г., Крамаренко Т.Н.

\"Мне приходится делить своё время между политикой и уравнениями. Однако уравнения по-моему, гораздо важнее, потому что политика существует только для данного момента, а уравнения будут существовать вечно\". А. Эйнштейн.

Здравствуйте, ребята! Повторим : Я - ваш помощник, я проведу вас по всей большой теме \" Квадратные уравнения\". В 7 и 8 классе вы уже рассматривали и даже решали квадратные уравнения.

Сегодня вы узнаете: 1. Какие уравнения называют квадратными? 2. Что в определении квадратного уравнения основное, что следует запомнить и учитывать? 3. Какие частные случаи квадратных уравнений бывают? 4. Каковы способы решения квадратных уравнений в каждом частном случае? А теперь давайте вместе искать ответы на эти вопросы. Желаю удачи!

Что общего у этих уравнений?

Квадратным уравнением называют уравнение вида … axІ + bx + c = 0, где а ≠ 0, х - переменная, а, в, с - некоторые числа. а–старший (первый) коэффициент, b-второй коэффициент, с-свободный член. а–старший (первый) коэффициент, b-второй коэффициент, с-свободный член. а – старший (первый) коэффициент, в - второй коэффициент, с - свободный член.

Если a = 1, то квадратное уравнение xІ + bx + c = 0 называют приведенным. Решим № 513 (устно).

а в с 5xІ + 5х – 3 = 0 3xІ + 2х – 4 = 0 хІ + 4х + 3 = 0 -2xІ + х – 1 = 0 4х І- 4х + 1 = 0 5 5 -3 3 2 -4 1 4 3 -2 1 -1 4 -4 1 Попробуем решить:

Интересно, а что будет, если коэффициенты квадратного уравнения по очереди или все сразу (кроме а) превратятся в нули. Давайте проведём исследование.

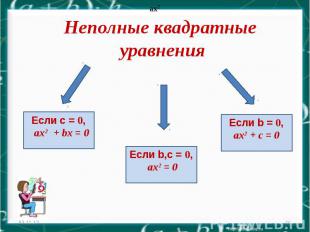
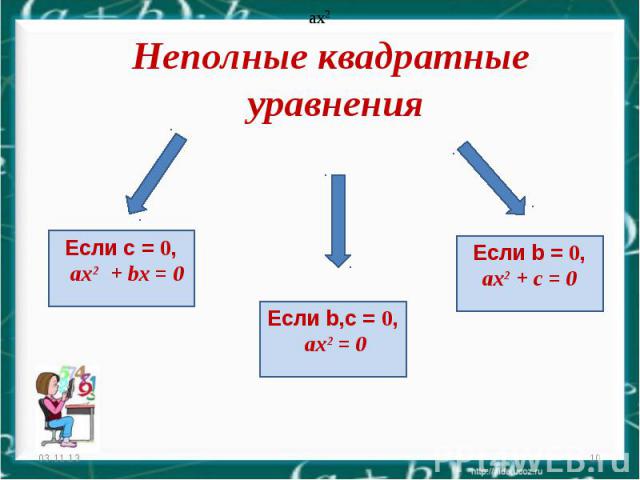
Неполные квадратные уравнения * * Если с = 0, ax2 + bх = 0 ax2 ax2 Если b,с = 0, ax2 = 0 Если b = 0, ax2 + c = 0

Рассмотрим все возможные случаи

Неполные квадратные уравнения вида

нет корней.

Неполные квадратные уравнения вида

Ответ: х=0. нет корней. Выпишите неполные квадратные уравнения:

Запишите квадратные уравнения с указанными коэффициентами: а=1, b=0, c=16; a=-1, b=5, c=0; b=0, a=-3, c=0; c=-8, a=1, b=0; a=1,5, c=0,b=-3; b= , a= , c Установите соответствие между уравнениями и следующими а) уравнение имеет два корня, б) уравнение имеет один корень, в) уравнение не имеет корней. (в) (а) (б) (а) (а) (а) Установите соответствие между уравнениями и следующими утверждениями:

* Проверьте решение № 515 (а, в, г). а).4х2-9=0 в). -0,1х2+10=0 г). 6v2+24=0 4х2 =9 -0,1х2 =-10 6v2 =-24 х2 =9/4 х2 =-10/(-0,1) v2 =-24/6 х1= -3/2=-1,5; х2=100 v2 =-4 х2 =3/2=1,5; х1= -10 Ответ: нет решения. Ответ:-1,5;1,5; Ответ:-10;10;

* * Рассмотрим решение неполных квадратных уравнений №517 (б, г, д) б). -5х2+ 6х=0 г). 4а2 - 3а=0 д). 6z2– z =0 х(-5х+6)=0 а(4а-3)=0 z(6z –1) =0 х=0 или -5х+6=0 а=0 или 4а-3=0 z=0 или 6z –1 =0 -5х= -6 4а=3 6z=1 х = -6/(-5) =1,2 а=3/4=0,75 z=1/6 Ответ: 0; 1,2. Ответ: 0; 0,75. Ответ: 0; 1/6.. .

1) При каких значениях а уравнение является квадратным уравнением? Нет решений 2) При каких значениях a уравнение является неполным квадратным уравнением ?

3) Решите уравнение при полученных значениях а. Ответ: а = −2, х= −15, х=0; а = 0,

Подведем итоги Какое же уравнение называется квадратным? Почему а≠0 ? Как называются числа а, в и с? Сколько видов неполных квадратных уравнений мы узнали? Как решают уравнения I вида? II вида? III вида?

Вот и завершается наш урок. Ребята! Вы получили ответы на интересующие вас вопросы? Поняли, что нас впереди ждут интересные, а самое главное – важные темы? Я только хочу вам напомнить, что при решении задач, примеров надо искать рациональные подходы и применять разнообразные способы.

Домашнее задание: П. 21 учебника; №№ 318, 321 а,в, 323 а. Дополнительно: 520, 532. П. 21 (определения), №518, 520 (а,в) 511 Дополнительно (для учащихся с повышенным интересом) №520, №531.