Презентация на тему: Неполные квадратные уравнения

Неполные квадратные уравнения

Математику нельзя изучать, наблюдая, как это делает сосед! А. Нивен

1. Какое уравнение называется квадратным? 2. Может ли коэффициент а в квадратном уравнении быть равным 0? Проверка знаний

3. Какое уравнение называется приведенным? 4. Какое уравнение называют полным? Не полным?

5. Укажите, какие из данных уравнений являются квадратными

Ответы Уравнение вида ax2+bx+c =0, где а, b, c –числа, а ≠0 Нет Уравнение вида x2+bx+c =0, (a = 1) Полным – Если b и с  ≠ 0 Не полным – Если b или c = 0, или оба коэффициента равны нулю а, в

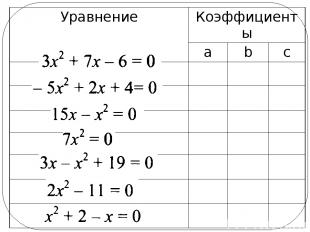
Уравнение Коэффициенты a b c

Составьте квадратное уравнение по его коэффициентам

Приведите уравнение к виду

Какие из данных уравнений являются приведенными? Не полными?

Решение неполных квадратных уравнений

1. Уравнение вида ax2=0, где а≠0 Пример1: 3,8x2=0 Разделим обе части уравнения на 3,8: x2=0 т.к. существует только одно число 0, квадрат которого равен 0, уравнение имеет единственный корень: х=0. Ответ: х=0.

Вывод: Уравнение вида ax2=0 (а≠0) имеет единственный корень х=0.

2. Уравнение вида ax2+с=0, где с≠0 Пример2: -3х2+15=0 Перенесем свободный член уравнения в правую часть Разделим обе части уравнения на -3 -3х2=-15, х2=5. Отсюда: Ответ:

Пример 3: 4х2+6=0 4х2+6=0, 4х2=-6, х2= т.к. квадрат числа не может быть отрицательным числом, то уравнение не имеет корней. Ответ: нет корней.

Вывод: Для решения уравнений вида ax2+с=0 (с≠0) воспользуемся алгоритмом: Перенесем свободный член с в правую часть уравнения. Делим обе части уравнения на а (с≠0), получаем уравнение: х2= ± Если >0, то уравнение имеет два корня: Если

3. Уравнение вида ах2+bх=0, где b≠0 5х2+7х=0 Разложим левую часть уравнения на множители: х(5х+7)=0 х=0 или 5х+7=0 5х=-7 х= х= -1,4 Ответ: х1=0, х2=-1,4

Вывод: Для решения уравнений вида ax2+bx=0 (b≠0) воспользуемся алгоритмом: Разложим левую часть уравнения на множители, получим x(ax+b)=0 Решаем уравнение ax+b=0, x= Уравнение имеет два корня: x1=0, x2=

Таблица для неполных квадратных уравнений:

Работа по учебнику № 519 (устно) № 518 № 523 (а, в)

Домашнее задание § 8, стр. 111-113 № 521 (а, в) № 522 (а, в) № 523 (б, г)

Желаю удачи в изучении алгебры!