Презентация на тему: Треугольник. Первый признак равенства треугольников

Треугольник. Первый признак равенства треугольников

ТРЕУГОЛЬНИК-это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки.

ТРЕУГОЛЬНИК и его элементы A, B, C – вершины, АВ, ВС, АС –стороны, A, В, С – углы. P∆ABC = AB + ВC + АC

№87 Начертите треугольник и обозначьте его вершины буквами М,N и P a) Назовите все углы и стороны ∆. б) С помощью линейки измерьте стороны треугольника и найдите периметр.

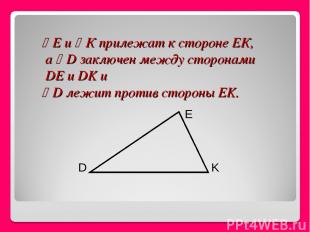
Е и К прилежат к стороне ЕК, а D заключен между сторонами DE и DK и D лежит против стороны EK.

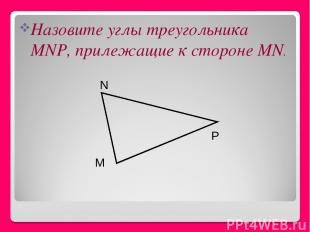
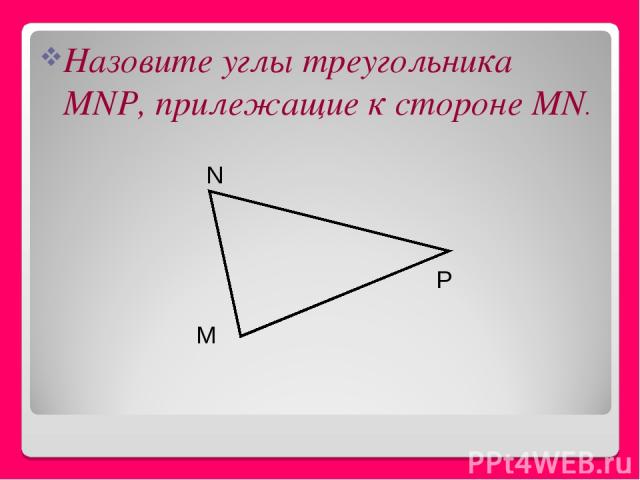
Назовите углы треугольника MNP, прилежащие к стороне MN. M P N

Назовите угол треугольника DEK, заключенный между сторонами DE и DK

Назовите угол треугольника MNP, заключенный между сторонами РN и РМ. M P N

Между какими сторонами треугольника DEK заключен угол К

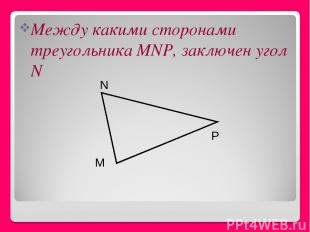
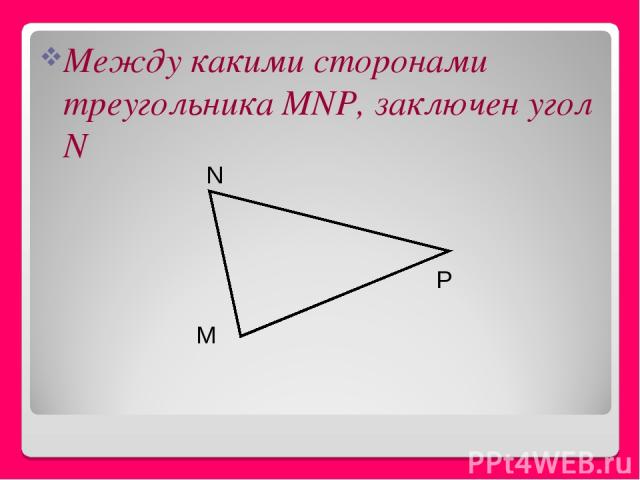
Между какими сторонами треугольника MNP, заключен угол N M P N

№88 Начертите треугольник DEF так, чтобы угол Е был прямой. Назовите: а) стороны, лежащие против углов D,Е,F б) углы, лежащие против сторон DE,EF,FD в) углы, прилежащие к сторонам DE,EF,FD.

№91 Периметр треугольника равен 48 см, а одна из сторон равна 18 см. Найдите две другие стороны, если их разность равна 4,6 см. № 92 Периметр одного треугольника больше периметра второго, могут ли быть равными эти треугольники? ОТВЕТ: нет, т. к. у равных фигур ВСЕГДА равны все элементы, в том числе и стороны. А периметр- это сумма всех этих сторон.

Теорема- это утверждение, справедливость которого устанавливается путем рассуждений, а сами рассуждения называются доказательством теоремы.

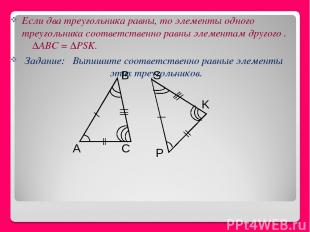
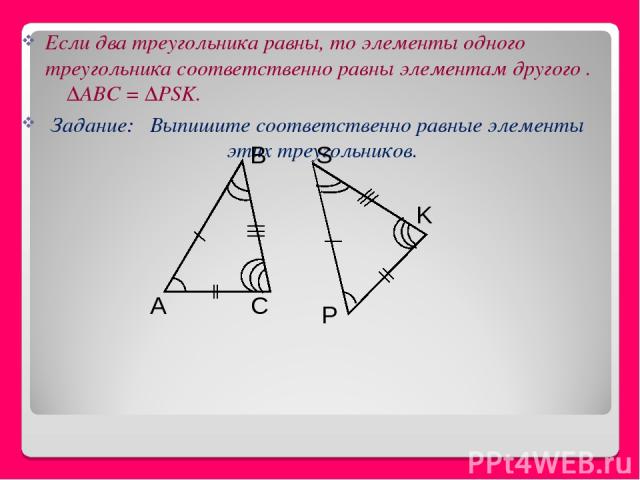
Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого . ∆ABC = ∆PSK. Задание: Выпишите соответственно равные элементы этих треугольников. S B A C P K

Для этого существуют три признака равенства треугольников Оказывается, что равенство двух треугольников можно установить не накладывая один треугольник на другой, а сравнивая только некоторые его элементы, так как на практике это наложение не возможно, например для двух земельных участков

ПЕРВЫЙ ПРИЗНАК РАВЕНСТВА ТРЕУГОЛЬНИКОВ Теорема: Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

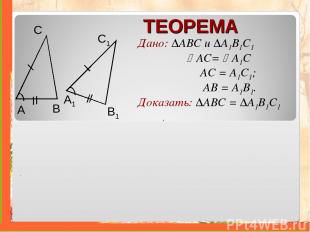
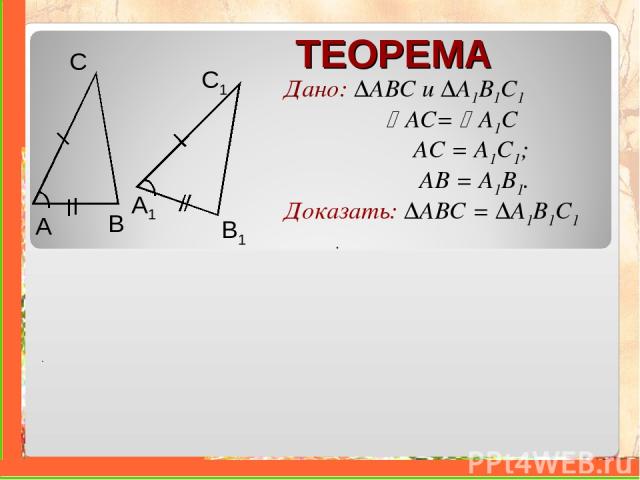
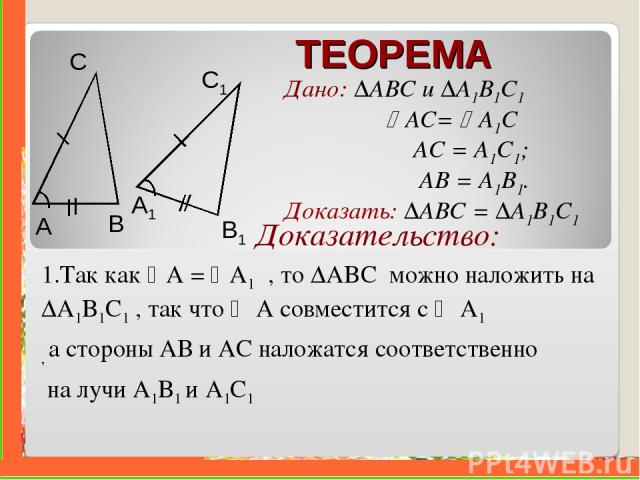
ТЕОРЕМА Дано: ∆ABC и ∆A1B1C1 AС= A1C AC = A1C1; AB = A1B1. Доказать: ∆ABC = ∆A1B1C1 A B С A1 B1 C1 . .

ТЕОРЕМА Дано: ∆ABC и ∆A1B1C1 AС= A1C AC = A1C1; AB = A1B1. Доказать: ∆ABC = ∆A1B1C1 A B С A1 B1 C1 Доказательство: 1.Так как A = A1 , то ∆ABC можно наложить на ∆A1B1C1 , так что А совместится с A1 , а стороны АВ и АС наложатся соответственно на лучи A1B1 и A1C1 .

ТЕОРЕМА Дано: ∆ABC и ∆A1B1C1 AС= A1C AC = A1C1; AB = A1B1. Доказать: ∆ABC = ∆A1B1C1 A B С A1 B1 C1 Доказательство: 2.Поскольку АВ = A1B1 , АС = A1C1 то сторона АВ совместится со стороной A1B1 , а сторона АС- со стороной A1C1, в частности, совместятся точки В и B1 , С и C1. Следовательно, совместятся стороны ВС и В1C1. .

ТЕОРЕМА Дано: ∆ABC и ∆A1B1C1 AС= A1C AC = A1C1; AB = A1B1. Доказать: ∆ABC = ∆A1B1C1 A B С A1 B1 C1 Доказательство: 1.Так как A = A1 , то ∆ABC можно наложить на ∆A1B1C1 , так что А совместится с A1 , а стороны АВ и АС наложатся соответственно на лучи A1B1 и A1C1 2.Поскольку АВ = A1B1 , АС = A1C1 то сторона АВ совместится со стороной A1B1 , а сторона АС- со стороной A1C1, в частности, совместятся точки В и B1 , С и C1. Следовательно, совместятся стороны ВС и В1C1. Итак, треугольники полностью совместятся, а значит они равны. .

РЕШЕНИЕ ЗАДАЧ Что известно о треугольниках MKT и EPF? Какой вывод можно сделать? M T K E F P

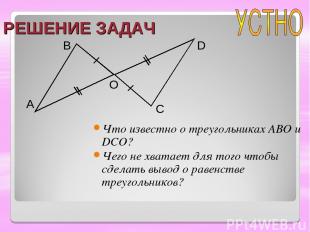
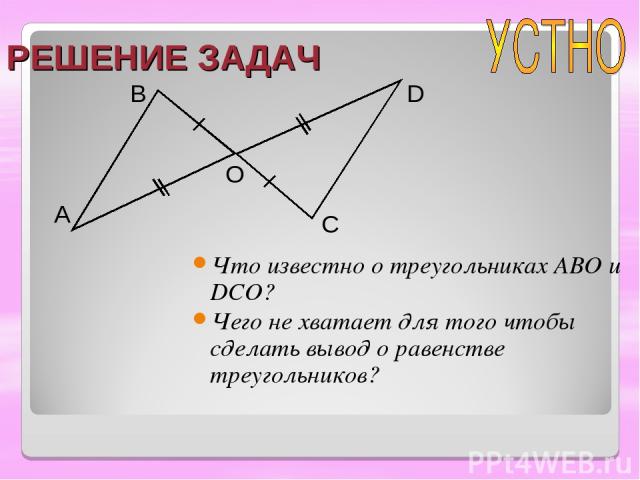
РЕШЕНИЕ ЗАДАЧ Что известно о треугольниках ABO и DCO? Чего не хватает для того чтобы сделать вывод о равенстве треугольников? A B O C D

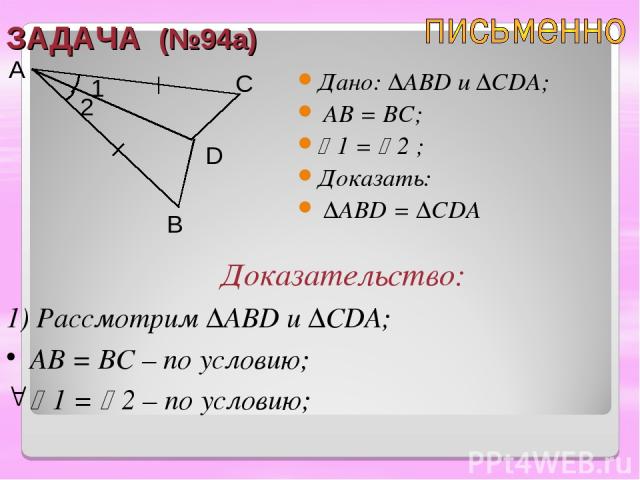
ЗАДАЧА (№94а) Дано: ∆ABD u ∆CDA; AB = BC; 1 = 2 ; Доказать: ∆ABD = ∆CDA A B C D Доказательство: 1) Рассмотрим ∆ABD и ∆CDA; AB = BC – по условию; 1 = 2 – по условию; 2 1

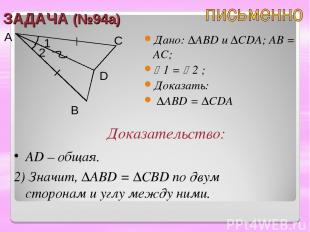
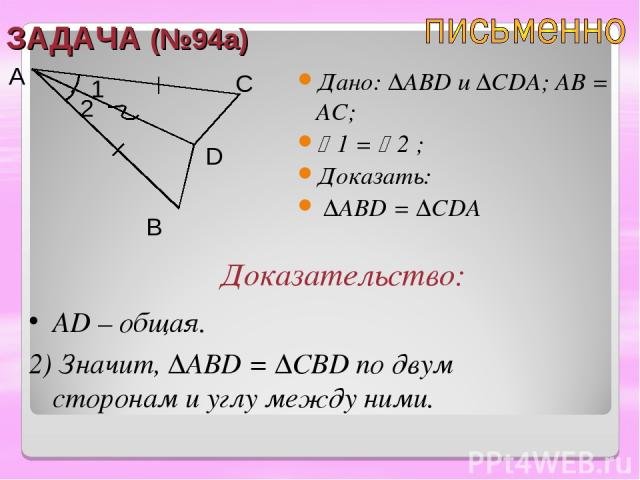
ЗАДАЧА (№94а) Дано: ∆ABD u ∆CDA; AB = АC; 1 = 2 ; Доказать: ∆ABD = ∆CDA A B C D Доказательство: АD – общая. 2) Значит, ∆ABD = ∆CBD по двум сторонам и углу между ними. 2 1

ЗАДАЧА (№95a) Дано: AD = BC; 1 = 2 ; Доказать: ∆ABC = ∆CDA. A B C D Доказательство: 1) Рассмотрим ∆ ABC и ∆CDA; AD = BC - по условию; 1 = 2 - по условию, AC – общая. 1 2

ЗАДАЧА (№95a) Дано: ВС = АD; 1 = 2 ; Доказать: ∆ABC = ∆CDA. A B C D Доказательство: 2) Значит, ∆ABC = ∆CDA по двум сторонам и углу между ними. 1 2

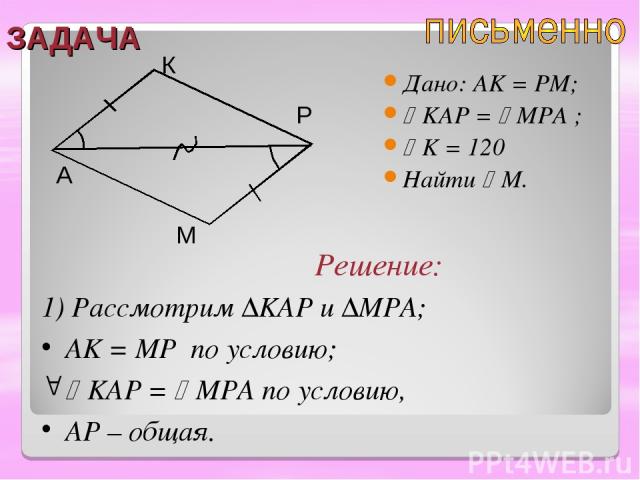
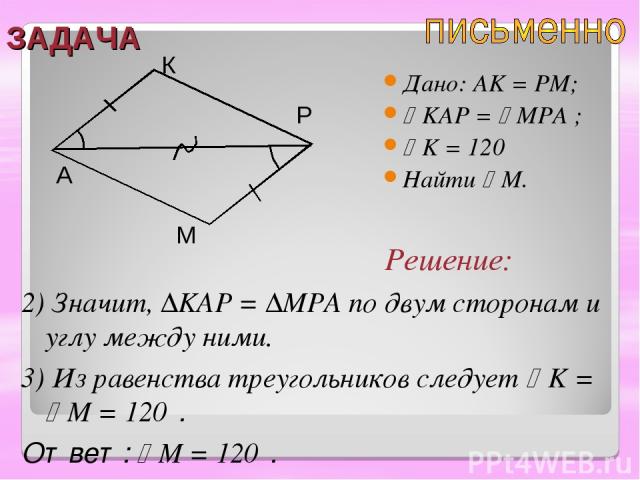
ЗАДАЧА Дано: AK = PM; KAP = MPA ; K = 120⁰ Найти M. A К Р М Решение: 1) Рассмотрим ∆KAP и ∆MPA; AK = MP по условию; KAP = MPA по условию, AP – общая.

ЗАДАЧА Дано: AK = PM; KAP = MPA ; K = 120⁰ Найти M. A К Р М 2) Значит, ∆KAP = ∆MPA по двум сторонам и углу между ними. 3) Из равенства треугольников следует K = M = 120⁰. Ответ: M = 120⁰. Решение:

Итог урока Перечислите виды треугольников, которые вы знаете. Какое утверждение называется теоремой? Что такое доказательство теоремы? Сформулируйте первый признак равенства треугольников.

ДОМАШНЕЕ ЗАДАНИЕ П14,15 вопросы 1-4 к главе 2 Теорему и доказательство учить; №90