Презентация на тему: Тела вращения

Геометрия. Тела вращения.

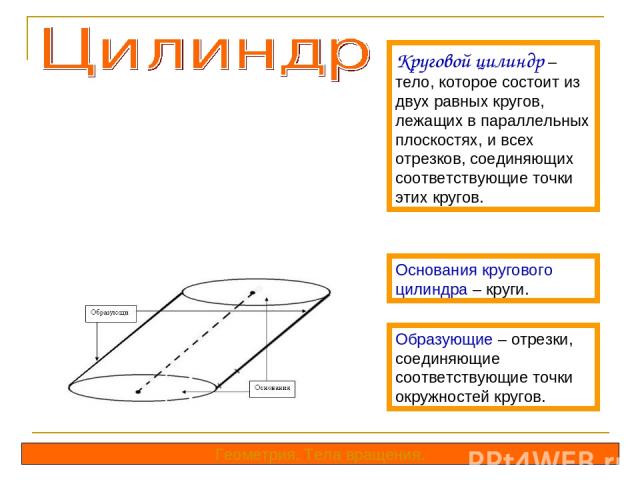
Круговой цилиндр – тело, которое состоит из двух равных кругов, лежащих в параллельных плоскостях, и всех отрезков, соединяющих соответствующие точки этих кругов. Основания кругового цилиндра – круги. Образующие – отрезки, соединяющие соответствующие точки окружностей кругов. Геометрия. Тела вращения.

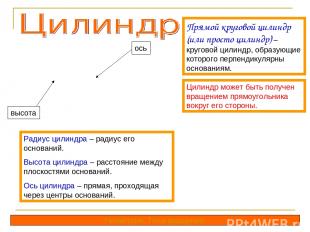
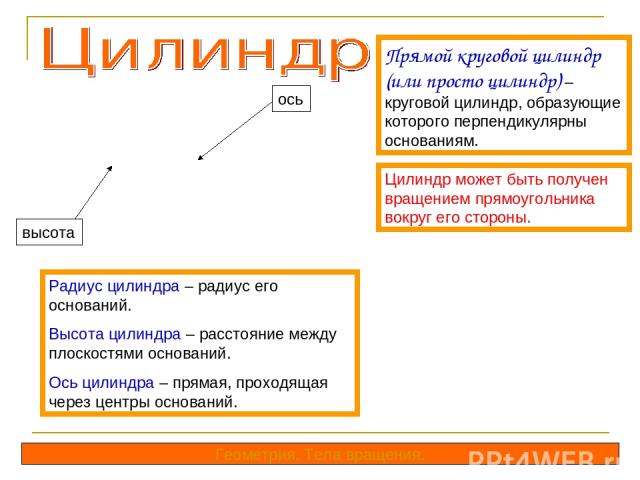
Прямой круговой цилиндр (или просто цилиндр) – круговой цилиндр, образующие которого перпендикулярны основаниям. Цилиндр может быть получен вращением прямоугольника вокруг его стороны. Радиус цилиндра – радиус его оснований. Высота цилиндра – расстояние между плоскостями оснований. Ось цилиндра – прямая, проходящая через центры оснований. ось высота Геометрия. Тела вращения.

Sбп = 2Пrh. Геометрия. Тела вращения. Sпп = Sбп + 2Sкр = 2Пrh + 2Пr = 2Пr(h + r). 2 Sпп = 2Пr(h + r).

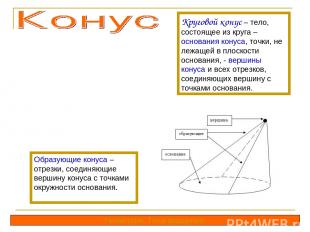
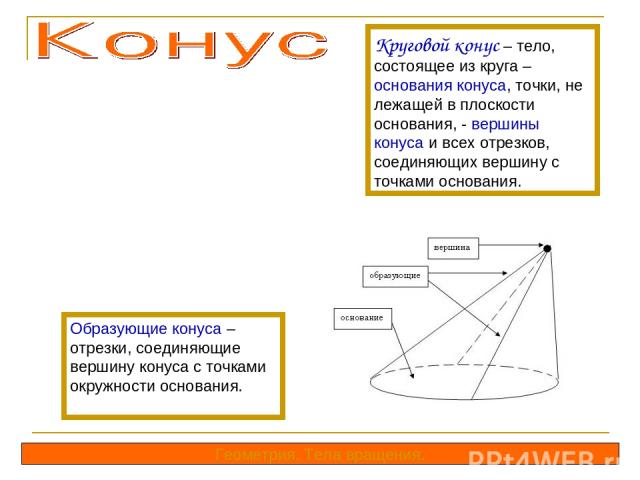
Круговой конус – тело, состоящее из круга – основания конуса, точки, не лежащей в плоскости основания, - вершины конуса и всех отрезков, соединяющих вершину с точками основания. Образующие конуса – отрезки, соединяющие вершину конуса с точками окружности основания. Геометрия. Тела вращения.

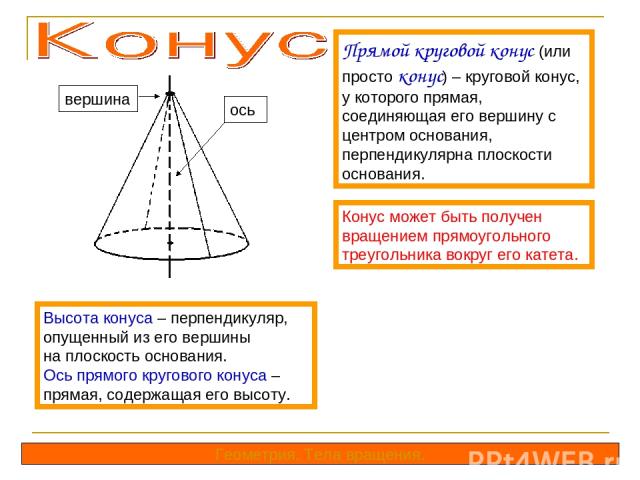
Прямой круговой конус (или просто конус) – круговой конус, у которого прямая, соединяющая его вершину с центром основания, перпендикулярна плоскости основания. Конус может быть получен вращением прямоугольного треугольника вокруг его катета. Высота конуса – перпендикуляр, опущенный из его вершины на плоскость основания. Ось прямого кругового конуса – прямая, содержащая его высоту. ось вершина Геометрия. Тела вращения.

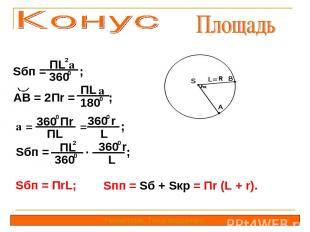
Sбп = ; ПL a 2 360 0 Геометрия. Тела вращения. AB = 2Пr = ; ПL a 180 0 a = = ; 360 Пr ПL 360 r 0 0 L Sбп = ; ПL 2 360 0 . 360 r 0 L Sбп = ПrL; Sпп = Sб + Sкр = Пr (L + r).

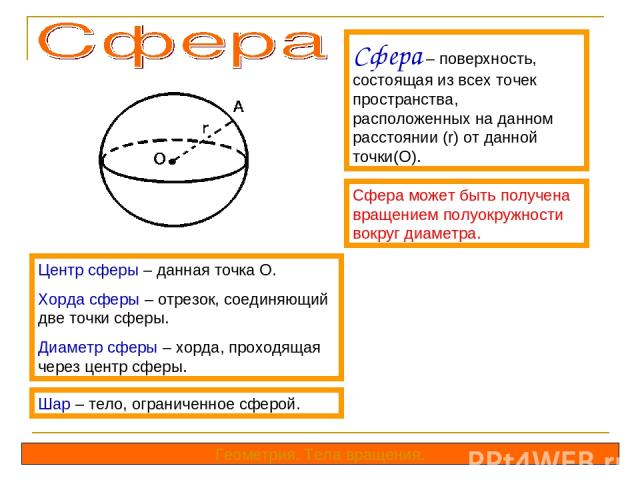
Геометрия. Тела вращения. Сфера – поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии (r) от данной точки(О). Сфера может быть получена вращением полуокружности вокруг диаметра. Центр сферы – данная точка О. Хорда сферы – отрезок, соединяющий две точки сферы. Диаметр сферы – хорда, проходящая через центр сферы. Шар – тело, ограниченное сферой.

S = 4Пr ; 2 Или S = ПD ; 2 Геометрия. Тела вращения.

Литература: Математика. Весь школьный курс в таблицах / авт.-сост. Т.С.Степанова. – Минск: Современная школа, 2007.