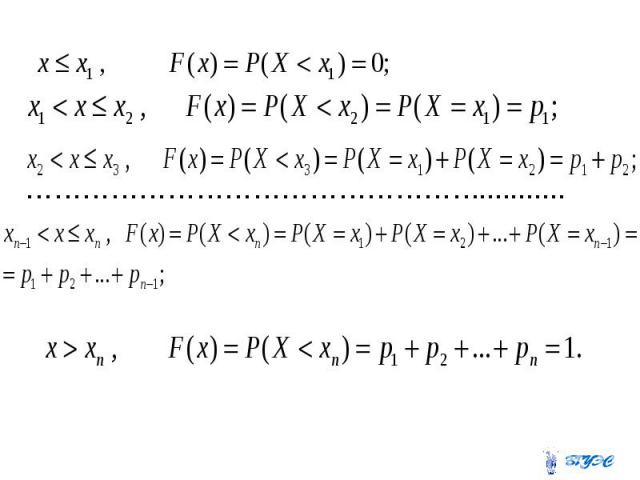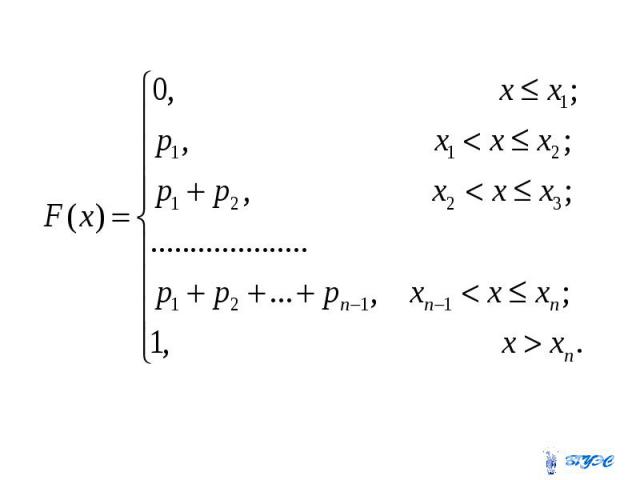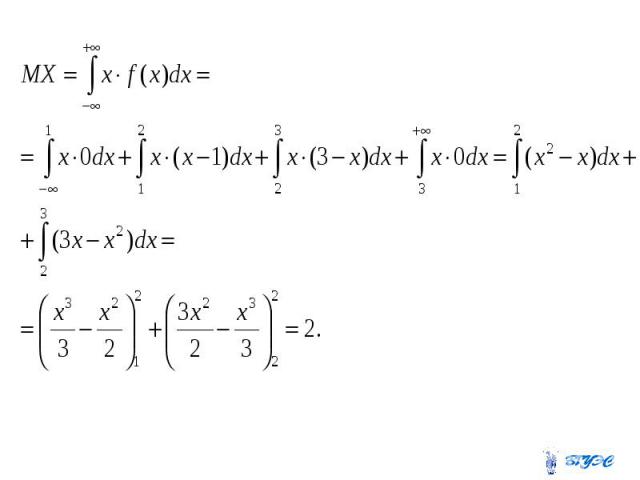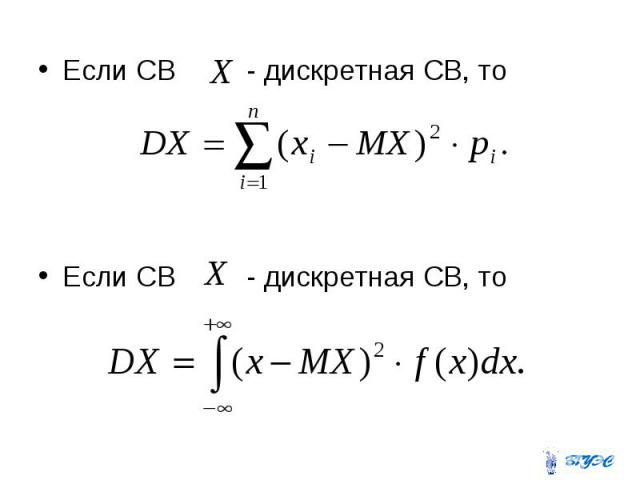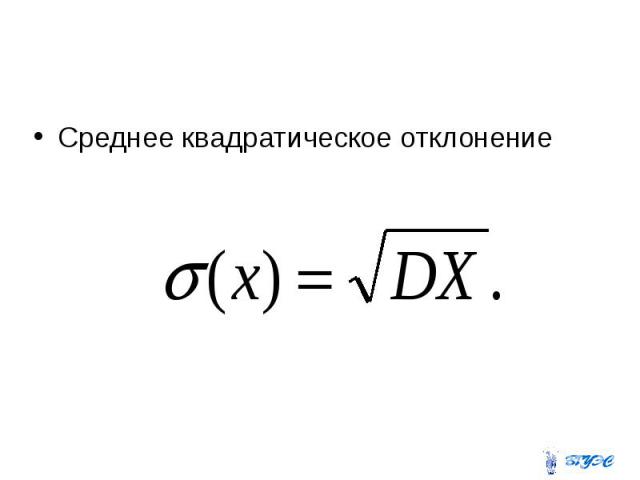Презентация на тему: Случайные величины и их числовые характеристики

Случайной называется величина, которая в результате опыта может принять то или иное возможное значение, неизвестное заранее, но обязательно одно.

Дискретной случайной величиной называют такую случайную величину, множество возможных значений которой либо конечно, либо бесконечно, но обязательно счетно.

Непрерывной случайной величиной называют такую случайную величину, которая может принять любое значение из некоторого конечного или бесконечного интервала.

Случайные величины: ; значения: .

Законом распределения дискретной случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

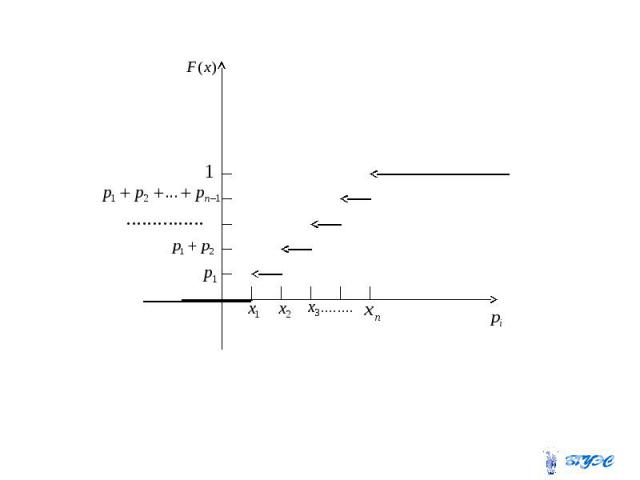
Закон распределения случайной величины можно задать, как и функцию: табличным, графическим и аналитическим способами.

Две случайные величины называются независимыми, если закон распределения вероятностей одной из них не зависит от того какие возможные значения приняла другая.

Если - функция распределения, Если - функция распределения, то Если - непрерывная случайная величина, то .

Если - дискретная случайная величина, то

…………………………………………...........

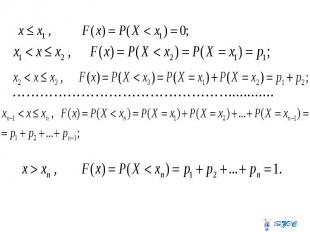
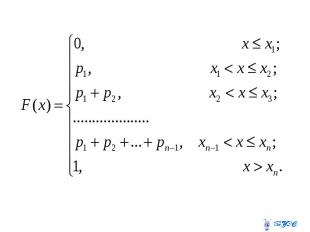
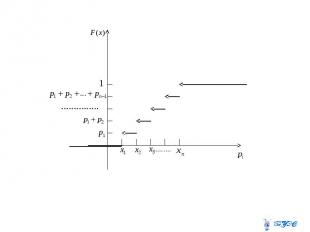
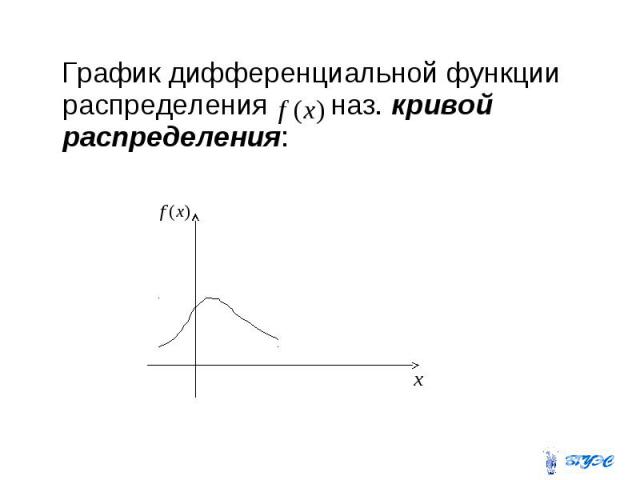
Дифференциальной функцией распределения или плотностью распределения вероятностей наз. первая производная интегральной функции распределения

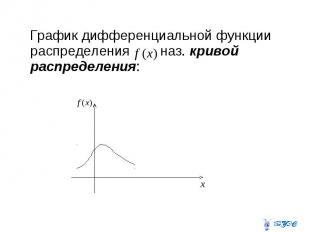
График дифференциальной функции распределения наз. кривой распределения: График дифференциальной функции распределения наз. кривой распределения:

1.Для 2.Для имеет место равенство 3. 4.

Числовые характеристики случайных величин.

Математическим ожиданием Математическим ожиданием дискретной случайной величины наз. сумма произведений всех возможных значений случайной величины на соответствующие вероятности появления этих значений:

Пусть случайная величина приняла значения Пусть случайная величина приняла значения Причем появилось раз, появилось раз, ………………………., появилось раз. где

Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат , называется Математическим ожиданием непрерывной случайной величины , возможные значения которой принадлежат , называется Если возможные значения принадлежат , то

Свойства математического ожидания Свойства математического ожидания 1. 2. 3.Если независимые случайные величины, то 4.Если независимые случайные величины, то 5.

Пример 1. Пример 1.

Пример 2.

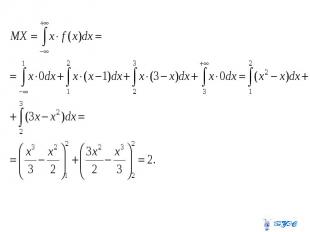
Дисперсия Математическое ожидание квадрата отклонения СВ от её математического ожидания называют дисперсией СВ :

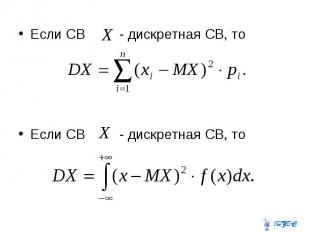
Если СВ - дискретная СВ, то Если СВ - дискретная СВ, то Если СВ - дискретная СВ, то

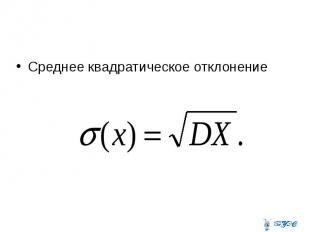
Среднее квадратическое отклонение

Свойства дисперсии 1. 2. 3. 4. 5.

Вопросы: Вопросы: 1)Определения дискретной случайной величины и непрерывной случайной величины? 2)Числовые характеристики ДСВ? 3)Числовые характеристики НСВ?