Презентация на тему: Ряды Тейлора (Маклорена)


Ряд вида называется рядом Тейлора для функции в точке . В частном случае при ряд принимает вид и называется рядом Маклорена.

Условие сходимости ряда Тейлора Для того чтобы бесконечно дифференцируемая в точке функция являлась суммой составленного для неё ряда Тейлора, необходимо и достаточно, чтобы Можно показать, что остаточный член можно представить в форме Лагранжа: , где некоторое число из интервала

Разложение некоторых элементарных функций в ряды Тейлора и Маклорена

Показательная функция Этот ряд сходится на всей числовой прямой.
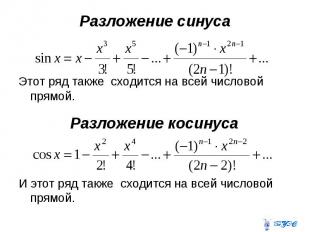
Разложение синуса Этот ряд также сходится на всей числовой прямой. И этот ряд также сходится на всей числовой прямой.

Биномиальный ряд Этот ряд называется биномиальным. Он сходится в интервале (-1,1). Это разложение имеет место для .

Вопросы: 1) Условие сходимости ряда Тейлора? 2)Какой ряд называется биномиальным?