Презентация на тему: Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MATHCAD

Автоматизация труда учителя на примере решения систем алгебраических уравнений с использованием программного пакета MatHCAD Автор Лагутина Марина Андреевна Руководитель проекта Учитель математики ГБОУ СОШ №237 Белкина Елена Геннадьевна

ЦЕЛИ РАБОТЫ Ознакомить учителей математики с возможностями продукта MathCAD Обеспечить автоматизацию работы учителей с использованием MathCAD Рассмотреть решение систем алгебраических уравнений с помощью MathCAD

Для кого эта РАБОТа Работа может применяться на факультативных занятиях и математических кружках Работа ориентирована на школьных учителей математики, в том числе проводящих факультативные занятия и математические кружки.

Содержание работы Работа разделена на две части: Предоставляет базовые знания работы с программой MathCAD Как они могут быть применены для решения СЛАУ и других типовых математических задач, часто встречаемых в ходе преподавания школьных дисциплин

Как решаются типовые задачи? Язык Fortran задачи линейной алгебры, интегрирование, решение дифференциальных уравнений Математические пакеты Mathematica Maple Matlab Mathcad

Почему Mathcad? Пакет MathCAD популярен, пожалуй, более в инженерной, чем в научной среде.

ПОЧЕМУ MATHCAD? Режим WYSIWYG Не требуется изучать какую-либо систему команд, как, например, в случае пакетов Mathematica или Maple Ориентирован на проведение численных расчетов Простота освоения Дружественный интерфейс

ЧТО УМЕЕТ MATHCAD?

ИНТЕрфейс MATHCAD

ОСНоВНЫЕ КОМАНДЫ

ПРАВИЛА НАБОРА КОМАНД 5^2=25

ПРАВИЛА НАБОРА КОМАНД

ПРАВИЛА НАБОРА КОМАНД

ТИПОВЫЕ ЗАДАЧИ Упростить выражение:

ПРАВИЛА НАБОРА КОМАНД Указатель мыши подводим к опции “Символы” в главном меню и щелкаем левой кнопкой мыши один раз (далее входим в “Символы”). В выпадающем меню указатель мыши подводим к опции “Упростить” и щелкаем на указанном пункте. На экране отображается наше выражение, но уже в выделенном виде. Повторяем наши действия: входим в “Символы” (подводим указатель мыши и щелкаем левой кнопкой мыши) и активизируем “Упростить”. На экране появляется ответ:

ТИПОВЫЕ ЗАДАЧИ Получаем ответ:

ТИПОВЫЕ ЗАДАЧИ Упростить выражение:

ТИПОВЫЕ ЗАДАЧИ Набираем на клавиатуре: X= 1.5 Y=-1.6 10x^2-5y^2=

ТИПОВЫЕ ЗАДАЧИ Получаем ответ:

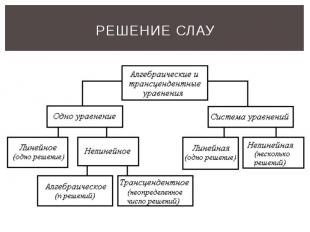
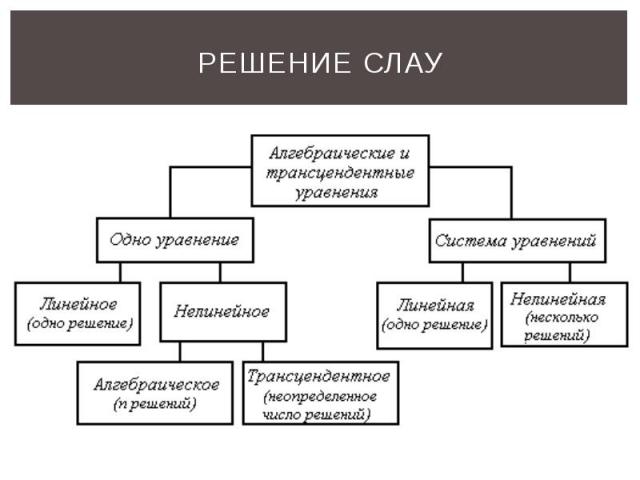
РЕШЕНИЕ СЛАУ

Способы решения СЛАУ Способы решения делятся на две группы: точные методы, представляющие собой конечные алгоритмы для вычисления корней системы (решение систем с помощью обратной матрицы, правило Крамера, метод Гаусса и др.), итерационные методы, позволяющие получить решение системы с заданной точностью путем сходящихся итерационных процессов (метод итерации, метод Зейделя и др.).

Способы решения СЛАУ Точные методы

Решение СЛАУ с помощью блока Given и функции Find MathCAD дает возможность решать системы уравнений. Максимальное число уравнений и переменных равно 50. Результатом решения системы будет численное значение искомого корня.

Решение СЛАУ с помощью блока Given и функции Find Системы линейных и нелинейных уравнений и неравенств позволяет решать блок given в сочетании с функцией Find. В блоке given записывается система уравнений и/или неравенств, подлежащих решению.

Решение СЛАУ с помощью блока Given и функции Find

Решение СЛАУ с помощью блока Given и функции Find Воспользуемся MathCAD и запишем систему в терминах блока «given - find»:

Решение СЛАУ матричным способом Матричным уравнением называется уравнение, коэффициенты и неизвестные которого – прямоугольные матрицы соответствующей размерности. Матричные уравнения можно разрешать только, если система не вырождена, то есть ее определитель отличен от нуля. Матричный способ более изящен (хотя и не самый эффективный с точки зрения вычислительной математики).

Решение СЛАУ матричным способом

Решение СЛАУ матричным способом Последовательность действий для решения с помощью Mathcad: Установите режим автоматических вычислений. Введите матрицу системы и матрицу-столбец правых частей. Вычислите решение системы по формуле x=A-1b. Проверьте правильность решения умножением матрицы системы на вектор-столбец решения. Найдите решение системы с помощью функции lsolve и сравните результаты.

Решение СЛАУ матричным способом Напишем код решения СЛАУ матричным способ на MathCAD. Также Решим систему с помощью функции lsolve и сравним результат с решением x=A-1b. С функцией lsolve мы сталкиваемся впервые, опишем ее: Lsolve(A,b) – возвращает вектор решения такой, что Ax=b. Аргументы: А - квадратная, не сингулярная матрица. b - вектор, имеющий столько же рядов, сколько рядов в матрице А.

Решение СЛАУ матричным способом

Решение СЛАУ методом Гаусса Метод Гаусса, его еще называют методом Гауссовых исключений, состоит в том, что систему приводят последовательным исключением неизвестных к эквивалентной системе с треугольной матрицей.

Решение СЛАУ методом Гаусса

Решение СЛАУ методом Гаусса Прямой ход метода Гаусса — элементарными операциями над строками приводят расширенную матрицу системы к ступенчатому виду:

Решение СЛАУ методом Гаусса Обратный ход метода Гаусса — ступенчатую матрицу преобразуют так, чтобы в первых n столбцах получилась единичная матрица: Последний, (n + 1) столбец этой матрицы содержит решение системы.

Решение СЛАУ методом Гаусса В MathCAD прямой и обратный ходы метода Гаусса выполняет функция rref(A). Далее показано решение системы линейных уравнений методом Гаусса, в котором используются следующие функции: Rref(A) - возвращается ступенчатая форма матрицы А. Augment(A,B) - Возвращается массив, сформированный расположением A и В бок о бок. Массивы A и В должны иметь одинаковое число строк

Решение СЛАУ методом Гаусса Последовательность действий: Функция augment(A,b) формирует расширенную матрицу системы добавлением к матрице системы справа столбца правых частей. Функция rref приводит расширенную матрицу системы к ступенчатому виду, выполняя прямой и обратный ходы гауссова исключения. Последний столбец содержит решение системы.

Решение СЛАУ методом Гаусса

Решение СЛАУ методом КРАМЕРА Последовательность действий: Вычисляем D определитель матрицы А. Зададим матрицу DX1, заменой первого столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX1. Зададим матрицу DX2, заменой второго столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX2. Зададим матрицу DX3, заменой третьего столбца матрицы А, матрицей b. Вычисляем определитель матрицы DX3. Определяем решение системы линейных уравнений x1, x2, x3.

Решение СЛАУ методом КРАМЕРА

Выводы Пакет MathCAD чрезвычайно интуитивен, т.к. все формулы в его документах записываются в традиционной форме, и как таковой язык программирования не применяется, а богатый пакет встроенных функций позволяет решать многочисленные задачи: разрешать уравнения и системы, раскладывать многочлены и решать неравенства, строить графики и т.д. Данная работа позволит ученикам и учителям быстро освоить основные навыки работы с пакетом MathCAD, а последовательные примеры и методы решения помогут их закрепить для решения новых задач.