Презентация на тему: Решение уравнений с модулями и параметрами

Решение уравнений с модулями и параметрами Учитель БОУ СОШ № 35 станицы Новотитаровской Динского района Краснодарского края Даниленко Лариса Андреевна

Цель урока. Решение уравнений с параметрами и модулями, применяя свойства функций в неожиданных ситуациях и освоение геометрических приемов решения задач. Нестандарные уравнения

Повторение важнейшего теоретического материала по теме: «Уравнения, содержащие модуль », Абсолютной величиной или модулем числа a называется число a, если a>0, число -a, если a<0, нуль, если a=0. Или a, если a>0 ׀ a ׀ ={ 0, если a=0 -a, если a<0Из определения следует, что ׀ a ׀≥ 0 и ׀ a ׀≥ a для всех a Є R Неравенство ׀ х ׀<a, (если a>0 ) равносильно двойному неравенству — a < х< a .Неравенство ׀ х ׀<a, (если a<0 ) не имеет смысла, так как ׀ х ׀ >0.Неравенство ׀ х ׀>a, (если a>0 ) равносильно двум неравенствам -Неравенство ׀ х ׀>a, (если a<0 ) справедливо для любого х Є R.

Повторение важнейшего теоретического материала по темам «Решение уравнений с параметрами» Решить уравнение с параметрами - значит указать, при каких значениях параметров существуют решения и каковы они.а) определить множество допустимых значений неизвестного и параметров;б) для каждой допустимой системы значений параметров найти соответствующие множества решений уравнения.

Устные упражнения. 1. Решить уравнение ׀ х-2 ׀ =5; Ответ 7;-3׀ х-2 ׀ =-5; Ответ решения нет׀ х-2 ׀ =х+5; ; Ответ решения нет; 1,5׀ х-2 ׀ = ׀ х+5 ׀ ; Ответ решения нет; -1,5; решения нет; -1,5;

2. Решить уравнение ах=1; Ответ . Если a=0, то нет решения; если a=0, то х=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения2) а = 1; получаем Ох = О , и очевидно х — любое. 1 3) если а =± 1 ,то х = —— а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1если а =± 1 ,то х= —— а-1

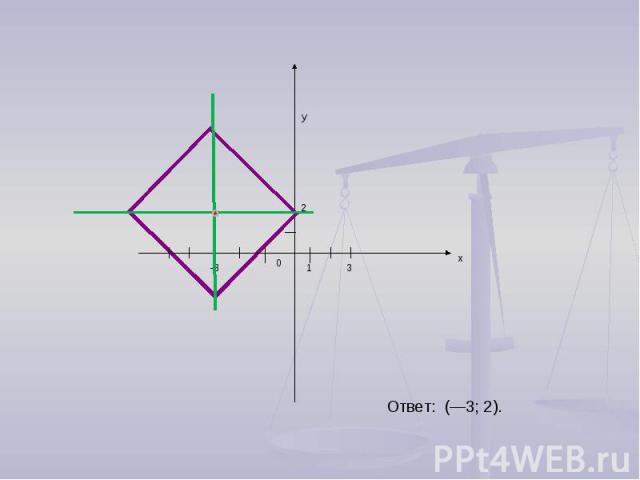
2.Решить уравнение ׀ х+3 ׀ + ׀ у -2 ׀= 4;

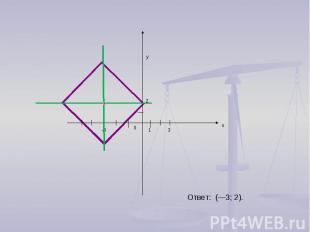
Ответ: (—3; 2).

2. Решить уравнение aх=1; Ответ. Если a=0, то нет решения; если a=0, то х=1/ a 1.3. Решить уравнение (а²-1) х = а+ 1. 1) а = 1; тогда уравнение принимает вид Ох = 2 и не имеет решения2) а = 1; получаем Ох = О , и очевидно х — любое. 1 3) если а =± 1 ,то х = —— а-1 Ответ. Если а=-1 , то х- любое; если а=1, то нет решения 1если а =± 1 ,то х= —— а-1

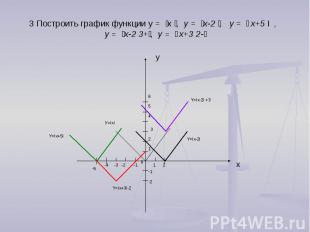
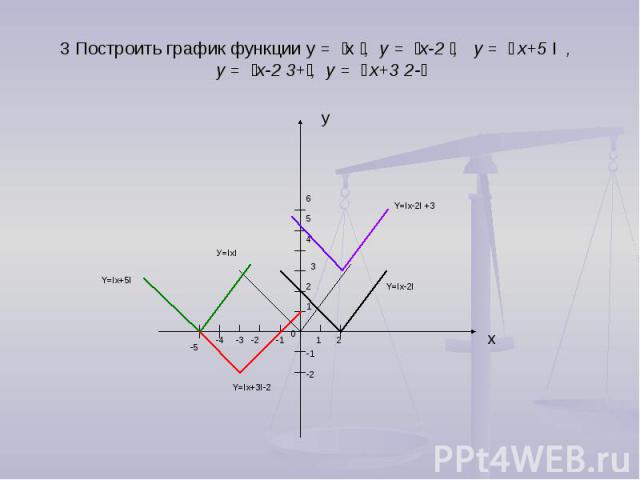
3 Построить график функции у = ׀х ׀, у = ׀х-2 ׀, у = ׀ х+5 I , у = ׀х-2 ׀+3, у = ׀ х+3 ׀-2

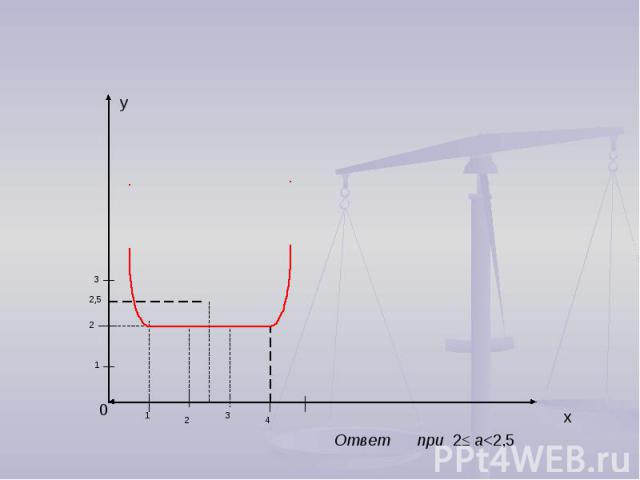
Решения примеров (из вариантов С) При каком значении параметра р уравнение ׀х²- 5х +6׀ + ׀х² - 5х +4׀ = α имеет четыре корня.

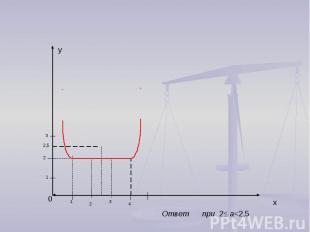
Ответ при 2≤ а<2,5

Самостоятельная работа по уровням. Итог урока. 1. Определение модуля.2.Что значит решить уравнение с параметрами?На дом. С 5 варианта №10 Ф.Ф. Лысенко Математика -2012 Спасибо за внимание

Спасибо за внимание