Презентация на тему: Решение уравнений высоких степеней

Курс предпрофильной подготовки "Решение уравнений высоких степеней" МОУ "Среднеахтубинская средняяобщеобразовательная школа №1"учитель математики высшей категорииЯицкая В. А.

Учащийся научится: - применять различные способы для разложенияна множители многочленов высоких степеней; - использовать полученные знания для решенияуравнений высоких степеней; - осуществлять поиск рационального способа разложения на множители или введения новой переменной для понижения степени уравнения с помощью удачной подстановки; - использовать специальную дополнительную литературу при выполненииразличных творческих заданий.

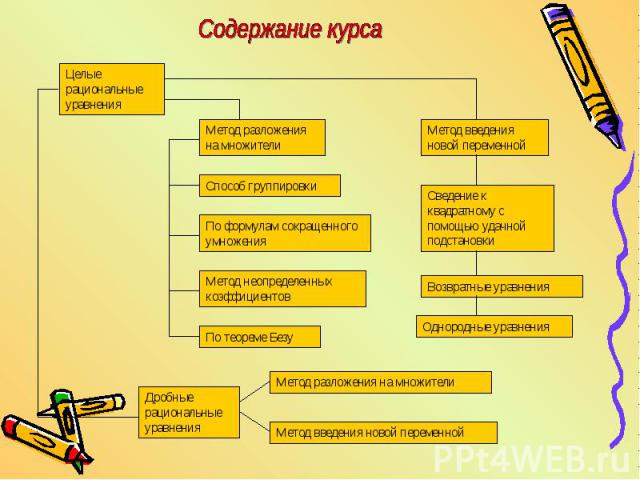
- Познакомить учащихся с различными способами разложения на множителимногочленов высоких степеней: группировки, с помощью формул сокращенного умножения, метода неопределенных коэффициентов, теоремыБезу и следствия из нее. - Научить понижать степень уравнения, используя теорему Безу и схему Горнера, а также удачную подстановку при введении новой пременной. - Изучить с учащимися способы решения возвратных иоднородных уравнений различных степеней с помощью специальной подстановки. - Научить учащихся решать дробные рациональныеуравнения используя метод разложения на множителии различные виды подстановок. - Познакомить учащихся со специальной научнойлитературой о жизни великих ученых и по истории математики.

Тематическое планирование Решение уравнений способомразложения на множители Решение уравнений способомвведения новой переменной.

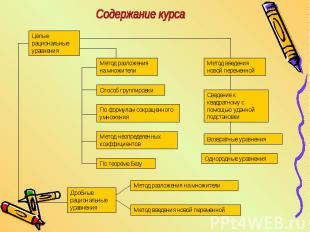
Содержание курса

В результате освоения данного курса учащиеся научатся: - раскладывать многочлен высокой степениразличными способами, что требуется выполнятьне только при решении уравнений; - различать основные виды уравнений и безошибочно определять способы их решения; - вводить новую переменную для упрощенияуравнения или понижения его степени; - вести самостоятельный поиск и отборинформации по теме курса, историческихсведений и интересных фактов из жизни великих ученых; - работать в рейтинговой программепо накоплению баллов

Уважаемые коллеги, Вы найдете очень много полезныхдополнений к программе курса в следующей литературе: Виленкин Н. Я. Алгебра для 8 и 9 классовАлгебра и математический анализ для 10 класса. "Просвещение" Галицкий М. Л. Сборник задач по алгебре для 8-9 классов,Углубленное изучение курса алгебры и математического анализа.Методические рекомендации дидактические материалы.Пособие для учителя Звавич Л. В., Аверьянов Д. И. Задания для проведения письменногоэкзамена по математике в 9 классе. Пособие для учителя. "Прсвещение" Иванов К. Б. Сборник задач для старшеклассников. Волгоград 2000. Кушнир И. Шедевры школьной математики. "Астарта" Сборник задач по математике для поступающих во ВТУЗы.Под ред. Сканави М. И.

Если Вас заинтересовала тема курса,то более подробно с содержанием можноознакомиться по электронномуили печатному вариантам. Спасибо за внимание!