Презентация на тему: Применение элементов математического анализа при решении задач

Применение элементов математического анализа при решении задач (по материалам ЕГЭ – 2010-2011)

Цели урока - Учиться проводить анализ условия задачи, что помогает поиску способа решения;- Учиться переводить язык задачи на язык производной или первообразной;- Учиться выстраивать цепочку логических рассуждений при переходе от языка функции к языку геометрии или механики

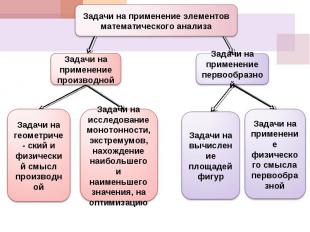
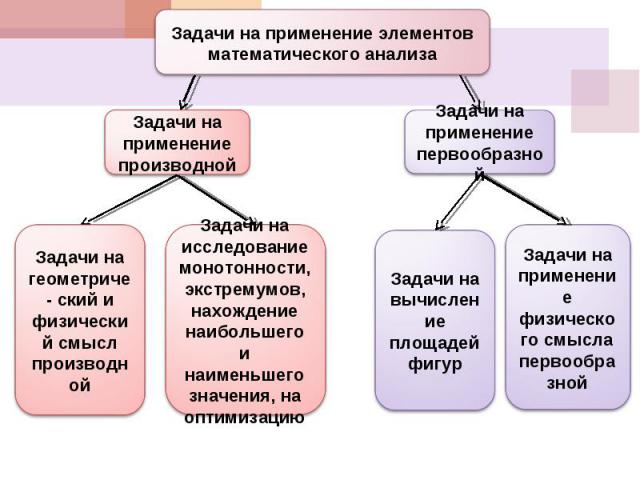
Задачи на применение элементов математического анализаЗадачи на применение производнойЗадачи на геометриче- ский и физический смысл производнойЗадачи на исследование монотонности, экстремумов, нахождение наибольшего и наименьшего значения, на оптимизациюЗадачи на применение первообразнойЗадачи на вычисление площадей фигурЗадачи на применение физического смысла первообразной

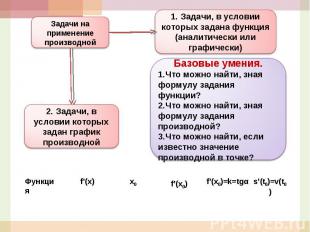
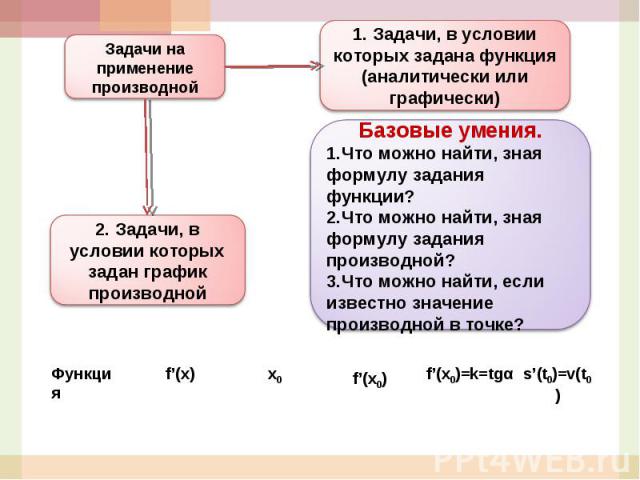
1. Задачи, в условии которых задана функция (аналитически или графически)Базовые умения.Что можно найти, зная формулу задания функции?Что можно найти, зная формулу задания производной?Что можно найти, если известно значение производной в точке?Задачи на применение производной2. Задачи, в условии которых задан график производной

Задание 1 Найдите угловой коэффициент касательной к графику первообразной функции F(x) функции f(x) = … в точке абсциссой …Что известно по условию задачи? Как задана функция?Что еще известно?Что нужно найти?Как находят тангенс угла наклона касательной, проведенной к графику заданной функции в заданной точке? 1б) Составьте задачу с другими числовыми данными, которая решается по плану: f’(x), f’(x0), k= f’(x0).

Задание 2Прочитайте задачу: В точке А графика функции у = 5x3+4x+1 проведена касательная к нему, параллельная прямой у = 4х + 3. Найдите сумму координат точки А. Обоснуйте следующий план решения задачи: к =4; f’(x); f’(x0) = 4; х0 из уравнения; ответ на вопрос задачи. Задание 3Что известно по условию задачи?(функция) Как задана функция?(формулой)Что еще известно?(х0)Что нужно найти?( к, tgα)Как находят тангенс угла наклона касательной, проведенной к графику заданной функции в заданной точке? Ответьте на вопросы анализа условия задачи на физический смысл производной: точка движется по координатной прямой по закону s(t) = t3/3 – 2t2+3t -15 (s- расстояние в см, t – время в секундах, прошедшее с момента движения). Определите скорость и ускорение точки через 3 с после начала движения.Что известно из условия задачи?Как задана функция?Что ещё известно?Что нужно найти?

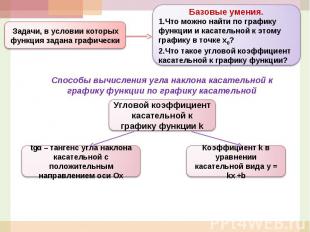
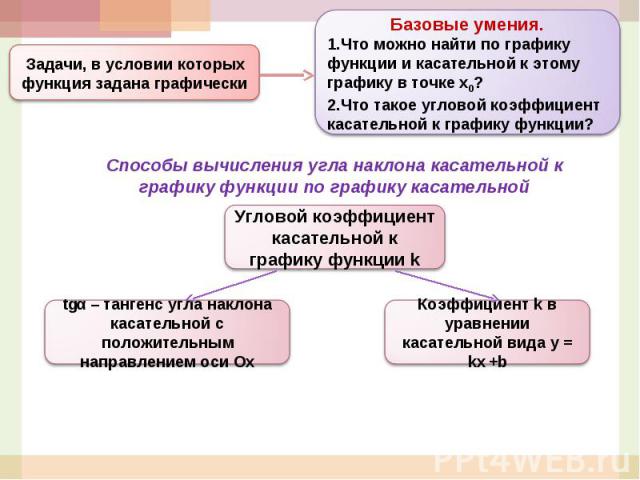
Базовые умения.Что можно найти по графику функции и касательной к этому графику в точке х0?Что такое угловой коэффициент касательной к графику функции?Задачи, в условии которых функция задана графическиСпособы вычисления угла наклона касательной к графику функции по графику касательнойУгловой коэффициент касательной к графику функции ktgα – тангенс угла наклона касательной с положительным направлением оси ОхКоэффициент k в уравнении касательной вида у = kx +b

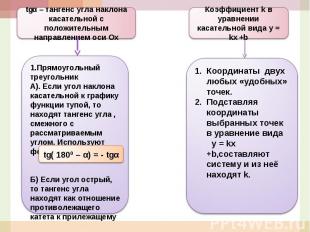
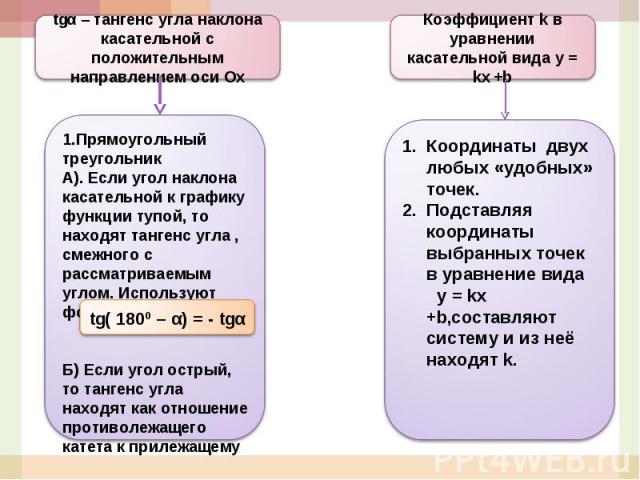
tgα – тангенс угла наклона касательной с положительным направлением оси Ох1.Прямоугольный треугольникА). Если угол наклона касательной к графику функции тупой, то находят тангенс угла , смежного с рассматриваемым углом. Используют формулу:Б) Если угол острый, то тангенс угла находят как отношение противолежащего катета к прилежащемуКоэффициент k в уравнении касательной вида у = kx +bКоординаты двух любых «удобных» точек.Подставляя координаты выбранных точек в уравнение вида у = kx +b,составляют систему и из неё находят k.

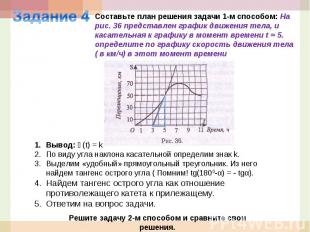
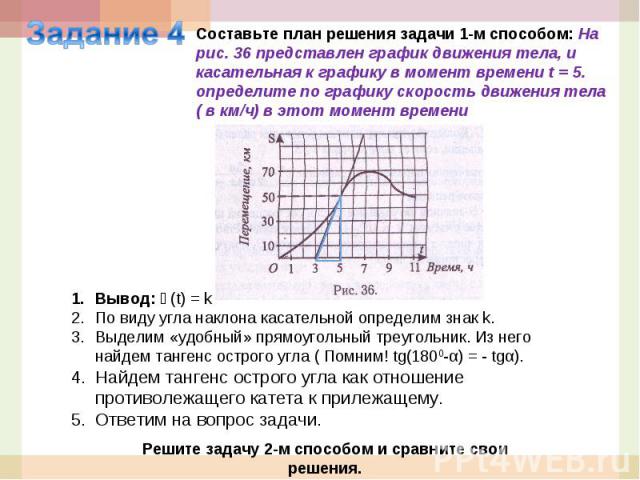
Задание 4Составьте план решения задачи 1-м способом: На рис. 36 представлен график движения тела, и касательная к графику в момент времени t = 5. определите по графику скорость движения тела ( в км/ч) в этот момент времениВывод: ϑ(t) = kПо виду угла наклона касательной определим знак k. Выделим «удобный» прямоугольный треугольник. Из него найдем тангенс острого угла ( Помним! tg(1800-α) = - tgα).Найдем тангенс острого угла как отношение противолежащего катета к прилежащему. Ответим на вопрос задачи.Решите задачу 2-м способом и сравните свои решения.

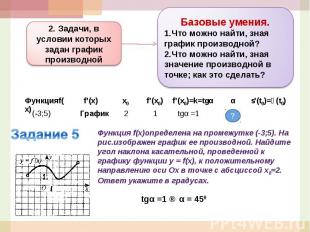
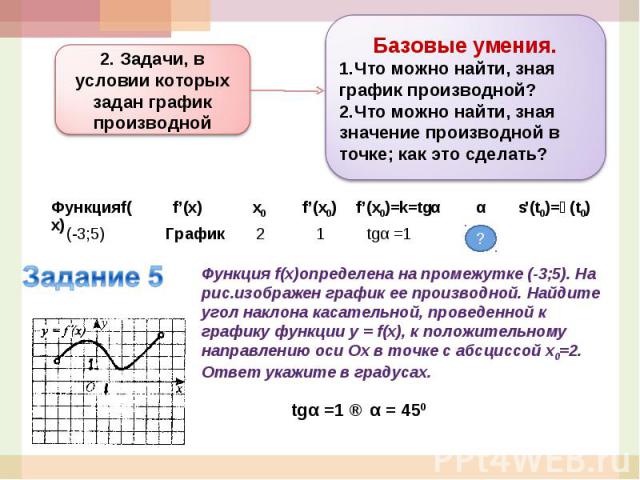
Базовые умения.Что можно найти, зная график производной?Что можно найти, зная значение производной в точке; как это сделать?2. Задачи, в условии которых задан график производнойФункция f(x)определена на промежутке (-3;5). На рис.изображен график ее производной. Найдите угол наклона касательной, проведенной к графику функции y = f(x), к положительному направлению оси Ох в точке с абсциссой х0=2. Ответ укажите в градусах.

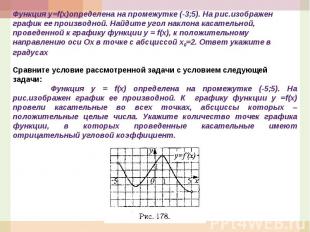
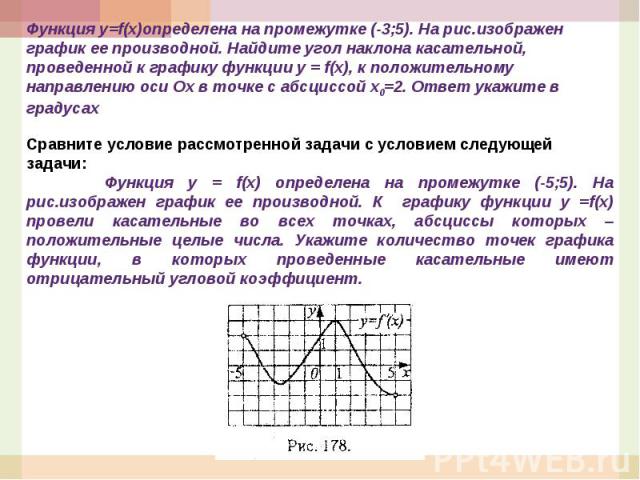
Функция у=f(x)определена на промежутке (-3;5). На рис.изображен график ее производной. Найдите угол наклона касательной, проведенной к графику функции y = f(x), к положительному направлению оси Ох в точке с абсциссой х0=2. Ответ укажите в градусахСравните условие рассмотренной задачи с условием следующей задачи: Функция у = f(x) определена на промежутке (-5;5). На рис.изображен график ее производной. К графику функции у =f(x) провели касательные во всех точках, абсциссы которых –положительные целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.

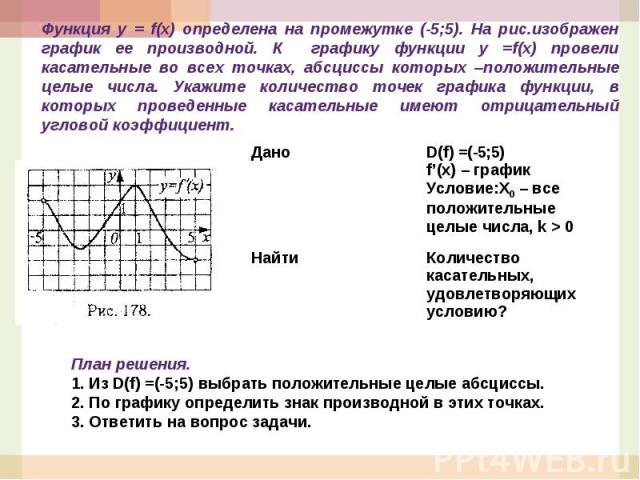
Функция у = f(x) определена на промежутке (-5;5). На рис.изображен график ее производной. К графику функции у =f(x) провели касательные во всех точках, абсциссы которых –положительные целые числа. Укажите количество точек графика функции, в которых проведенные касательные имеют отрицательный угловой коэффициент.План решения. 1. Из D(f) =(-5;5) выбрать положительные целые абсциссы.2. По графику определить знак производной в этих точках.3. Ответить на вопрос задачи.

Функция у = f(x) определена на промежутке (-3;5). На рис.изображен график ее производной. Укажите количество точек графика функции, в которых касательные наклонены под углом 1500 к положительному направлению оси абсцисс.α =1500, tg α < 0, k<0, f’(x0)<0. Чтобы ответить на вопрос задачи … Используем метод оценки: tg 450< tg500 < tg 600, 1<tg500<√3Найти значение тангенса угла по значению косинуса угла

Использованная литература Материалы курсов повышения квалификации при Брянском государственном университете имени академика И.Г.Петровского