Презентация на тему: Решение иррациональных неравенств (11 класс)

Решение иррациональных неравенств 11 класс Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной УМК: любой

Содержание Теория: - определение - свойства - способы решения Задания для решения вместе Задания для самостоятельной работы Задания для работы в парах

Теория Иррациональными называются неравенства, содержащие переменную под знаком корня При решении иррациональных неравенств надо находить ОДЗ, т.к. сделать проверку труднее Если обе части неравенства не отрицательны, то их можно возвести в четную степень и знак неравенства при этом не изменится Неравенство можно возвести в нечетную степень не проверяя не отрицательность левой части.

Теория Основным методом решения иррациональных неравенств является сведение его к системе неравенств или к совокупности систем неравенств. Чаще всего используются следующие случаи: А)
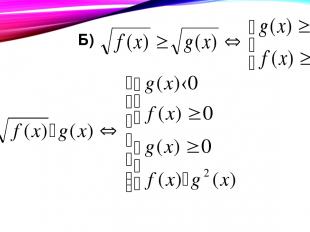
Б) В)
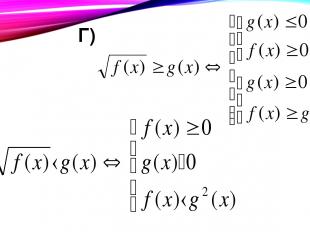
Г) Д)

Е) то неравенство не имеет решения Ж)

Решаем 1) 2) 3) 4) 5) 6)
![Самостоятельная работа 1) 2) Ответ: [-4;5] Ответ: Самостоятельная работа 1) 2) Ответ: [-4;5] Ответ:](https://fs3.ppt4web.ru/images/132017/192774/310/img8.jpg)
Самостоятельная работа 1) 2) Ответ: [-4;5] Ответ:

Работа в парах 1) 2) Ответ: (-∞;-1)u(9;+∞) Ответ: (-1;0)u(3;4)

ИСПОЛЬЗУЕМЫЕ ИСТОЧНИКИ Ш.А.Алимов и др. «Алгебра и начала анализа» 10-11 кл., М., Просвещение, 2003г. Автор, заимствованного шаблона, неизвестен http://upload.wikimedia.org/wikipedia/commons/thumb/3/3e/Nuvola_apps_edu_mathematics_blue-p.svg/800px-Nuvola_apps_edu_mathematics_blue-p.svg.png http://hijos.ru/wp-content/uploads/2013/02/number36_1.jpg





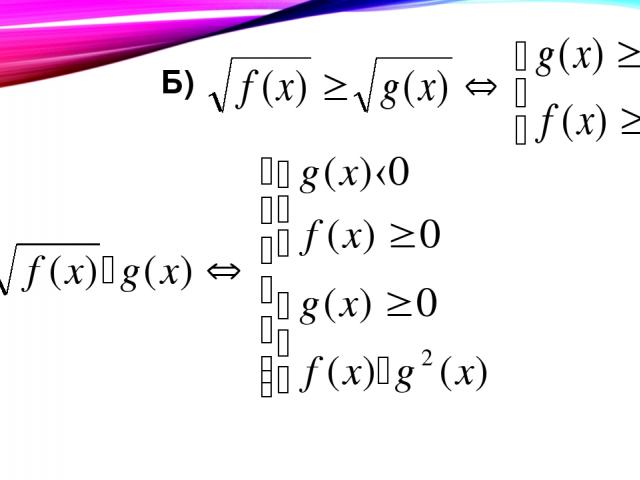
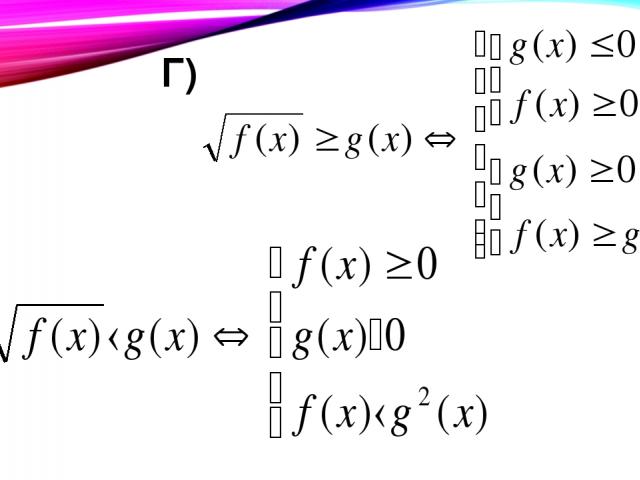


![Самостоятельная работа 1) 2) Ответ: [-4;5] Ответ: Самостоятельная работа 1) 2) Ответ: [-4;5] Ответ:](https://fs3.ppt4web.ru/images/132017/192774/640/img8.jpg)













