Презентация на тему: Пропорции (11 класс)

Творческий проект по математикена тему: "Пропорции"ученица 11 класса Ефремова Юлияучитель математики Щербакова Г.Н.

Вступление "Впервые интерес к пропорции, возникающей при делении отрезка в крайнем и среднем отношении, возникает в античной науке (Пифагор, Платон, Евклид). Удивительные математические свойства этой пропорции уже тогда создают вокруг нее ореол таинственности и мистического поклонения".

Пропорция Слово «пропорция» (от латинского propotio) означает «соразмерность», «определённое соотношение частей между собой». В математике: равенство двух отношений

Возникновение учений об отношениях и пропорциях. Учение об отношениях и пропорциях особенно успешно развивалось в IV веке до нашей эры в Древней Греции, славившейся произведениями искусства, архитектуры, различными ремеслами. С пропорциями связывались представления о красоте, порядке и гармонии, о созвучных аккордах в музыке.

Основное свойство пропорций Теория отношений и пропорций была подробно изложена в «Началах» Евклида (III век до нашей эры), там, в частности, приводится и доказательство основного свойства пропорции. Оно звучит так: «В верной пропорции произведение крайних членов равно произведению средних. a : b = c : d

ПРОПОРЦИОНАЛЬНОСТЬ Это простейший вид функциональной зависимости. Различают прямую пропорциональность. ( y = kx) и обратную пропорциональность ( y= k/ x). Напр., путь S, пройденный при равномерном движении со скоростью v, пропорционален времени t, т. е. S = vt ; прямо пропорциональна величина основания y прямоугольника с заданной площадью a обратно пропорциональна высоте x, т. е. y = a/ x.

Свойства прямой пропорциональной зависимости Каждому значению х соответствует единственное определенное значение у. (первое свойство прямой пропорциональной зависимости) Отношение соответствующих значений величин у и х, связанных прямой пропорциональностью, равно коэффициенту пропорциональности.Если две величины связаны между собой прямой пропорциональной зависимостью, то при увеличении (уменьшении) одной из них в несколько раз значение другой увеличивается (уменьшается) во столько же раз.Математической моделью прямой пропорциональной зависимости величин х и у является формула у = кх

Свойства обратной пропорциональной зависимости Каждому значению х (за исключением х=0) соответствует вполне определенное значение у.Произведение соответствующих значений х и у равно коэффициенту обратной пропорциональности.Если х увеличивается (уменьшается) в несколько раз, то у уменьшается (увеличивается) во столько же раз, так как их произведение остается неизменным. Если х и у связаны обратной пропорциональной зависимостью, то отношение двух любых значений величины х равно обратному отношению соответствующих значений у:

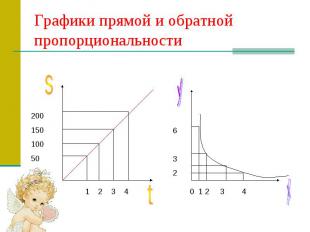
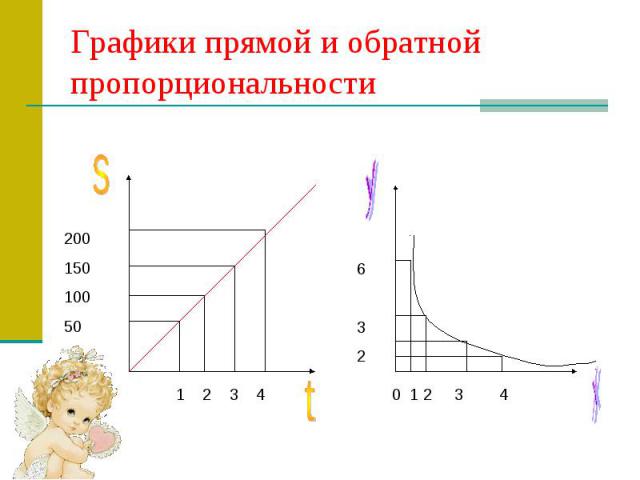
Графики прямой и обратной пропорциональности

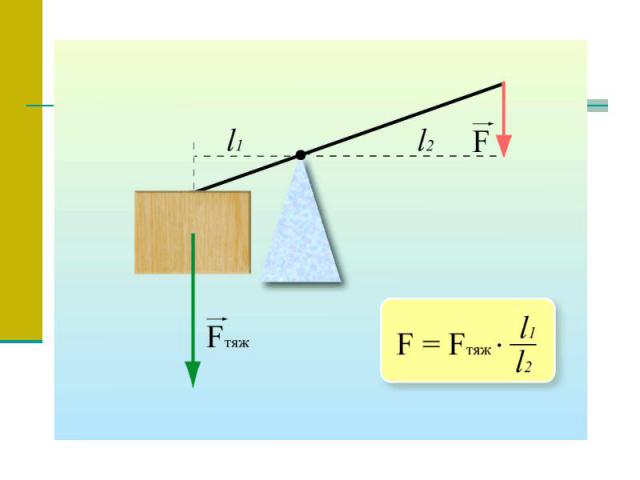
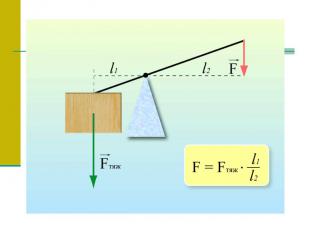
Пропорции в физике С глубокой древности люди пользовались различными рычагами. Весло, лом, весы, ножницы, качели, тачка и т.д. – примеры рычагов. Выигрыш, который дает рычаг в прилагаемом усилии, определяется пропорцией, где M и m – массы грузов, а L и l – «плечи» рычага.

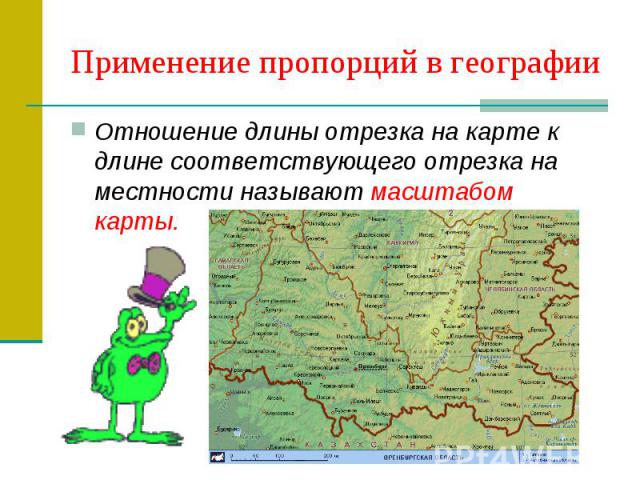
Применение пропорций в географии Отношение длины отрезка на карте к длине соответствующего отрезка на местности называют масштабом карты.

Пропорциональность в других сферах жизни Пропорциональность в природе, искусстве, архитектуре означает соблюдение определенных соотношений между размерами отдельных частей растения, скульптуры, здания и является непременным условием правильного и красивого изображения предмета.

Золотое сечение Золотым сечением и даже «божественной пропорцией» называли математики древности и средневековья деление отрезка, при котором длинна всего отрезка так относится к длине его большей части, как длинна большей части к меньшей. Приближенно это отношение равно 0, 618 ≈5/8. Золотое сечение чаще всего применяется в произведениях искусства, архитектуре, встречается и в природе.

Применение «золотого сечения» в архитектуре ПАРФЕНОН, храм Афины Парфенос на Акрополе в Афинах, памятник древнегреческой высокой классики. Мраморный дорический периптер с ионическим скульптурным фризом (447-438 до н. э., архитекторы Иктин и Калликрат) замечателен величественной красотой форм и пропорций. Статуи фронтонов, рельефы метоп и фриза (окончены в 432 до н. э.) созданы под руководством Фидия. Разрушен в 1687; частично восстановлен. Отношение высоты здания к его длине равно 0, 618.

«Золотое сечение» в искусстве АПОЛЛОН БЕЛЬВЕДЕРСКИЙ, статуя Аполлона — мраморная римская копия бронзового оригинала работы древнегреческого скульптора Леохара (ок. 330-320 до н. э., Музей Пио-Клементино, Ватикан). Название от ватиканского дворца Бельведер, где выставлена статуя. Долгое время считалась вершиной греческого искусства. На рисунке представлена статуя Аполлона Бельведерского, разделенная в отношении (точка С делит отрезок АD, точка В делит отрезок АС)

Окружающие предметы также часто дают примеры золотого сечения. Например, переплеты многих книг имеют отношение ширины и длинны, близкое к 0,618.

Рассматривая расположение листьев на общем стебле растений, можно заметить, что между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (точка В).

Задача О применении математики в языкознании  В классе заболел учитель русского языка. Пришёл математик и стал объяснять падежи: Именительный       кто ?        что ? Родительный          кого ?       чего ? Дательный              кому ?      а второй вопрос он забыл.   Тогда он сказал: - Ничего, давайте обозначим его через  x  и составим пропорцию:  Итак, второй вопрос дательного падежа:  чему ?

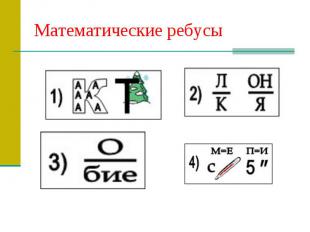
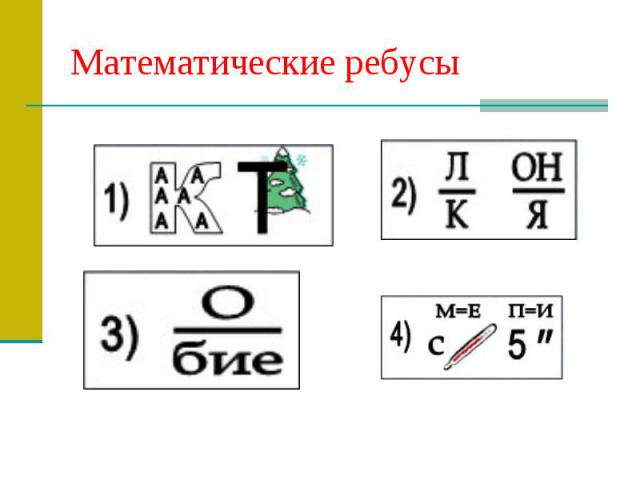
Математические ребусы

1.Показатель2. Наклоная3.Подобие4.Стереометрия

Заключение Пропорции сопровождают нас повсюду и являются неотъемлемой частью нашей жизни. В своей презентации я привела только не большой перечень сфер где применяют пропорции. На самом деле этот список намного больше. Ведь пропорции появились одновременно с природой, даже до появления человека.

Спасибо за внимание!