Презентация на тему: Прямоугольный треугольник

Три вершины тут видны, Три угла, три стороны,- Ну, пожалуй, и довольно! Что мы видим?

Викторина 180 1800 равносторонний Сумма углов треугольника равна Треугольник, в котором три стороны равны Каждый угол равностороннего треугольника равен 600

Викторина 180 гипотенуза катет Если в треугольнике два угла равны, то треугольник Сторона прямоугольного треугольника, лежащая против прямого угла Сторона прямоугольного треугольника, прилежащая к прямому углу равнобедренный

Свойство 1 Сумма двух острых углов прямоугольного треугольника равна 900 А В С B + C = ? 900

Свойство 2 Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы А В С D Дано: АВС А = 900 В = 300 Доказать: 300 300 600 Доказательство: ВСD : D = В = 600, DC = BC

Свойство 3 Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300 А В С D Дано: АВС А = 900 Доказать: Доказательство: ВСD - равносторонний DВС = 600, DC = BC АВС = 300 DВС = 2 АВС, АВС = 300

Свойства прямоугольного треугольника Сумма двух острых углов прямоугольного треугольника равна 900 Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300

Каждой команде предлагается по очереди ответить на вопрос (решить задачу). Будьте внимательными, так как вопросы адресованы всему классу. Если команда дает верный ответ, то это значит, что она забила гол в ворота соперников Если команда не может ответить на вопрос или дает неверный ответ, то право ответа переходит к команде соперников.

380 ? В С А

В С А ? ?

15 см ? 300 А В С

4 см ? 300 А В С

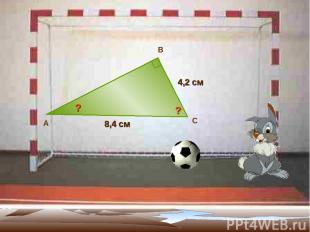
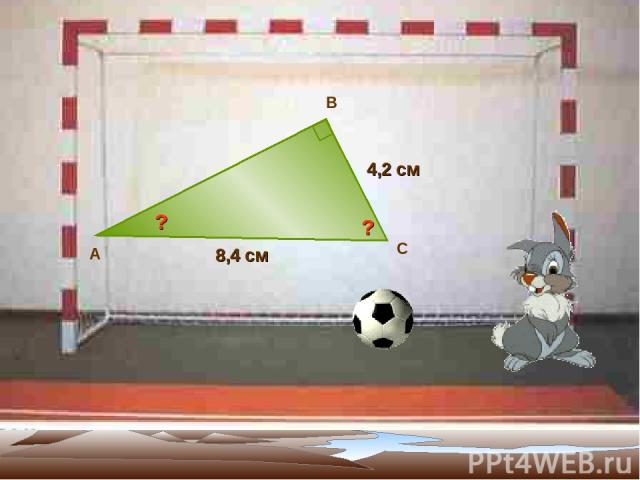
8,4 см А В С 4,2 см ? ?

? 700 А В С D

Признаки равенства прямоугольных треугольников Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. 2. Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны. 3. Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. 4. Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны.

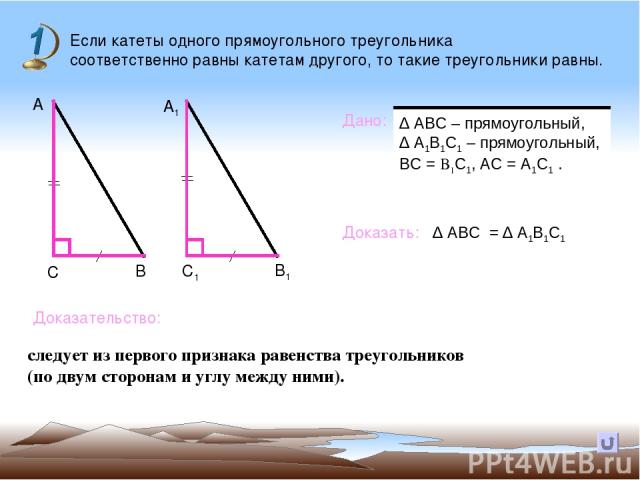
Если катеты одного прямоугольного треугольника соответственно равны катетам другого, то такие треугольники равны. Дано: Доказать: Доказательство: В А А1 С С1 В1 ∆ АВС = ∆ А1В1С1 следует из первого признака равенства треугольников (по двум сторонам и углу между ними).

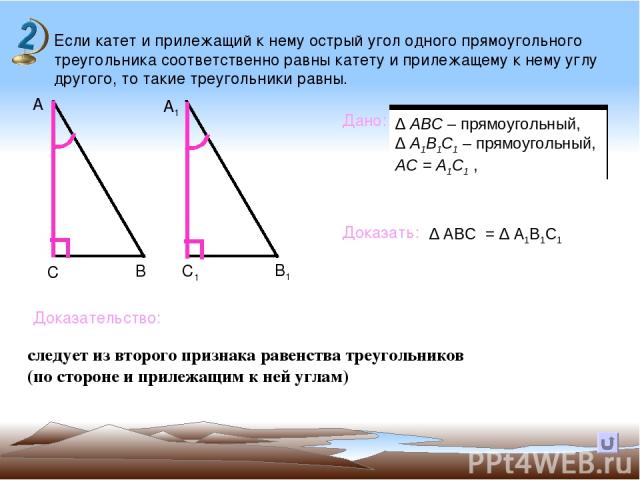
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему углу другого, то такие треугольники равны. В А А1 С С1 В1 Дано: Доказать: Доказательство: следует из второго признака равенства треугольников (по стороне и прилежащим к ней углам) ∆ АВС = ∆ А1В1С1

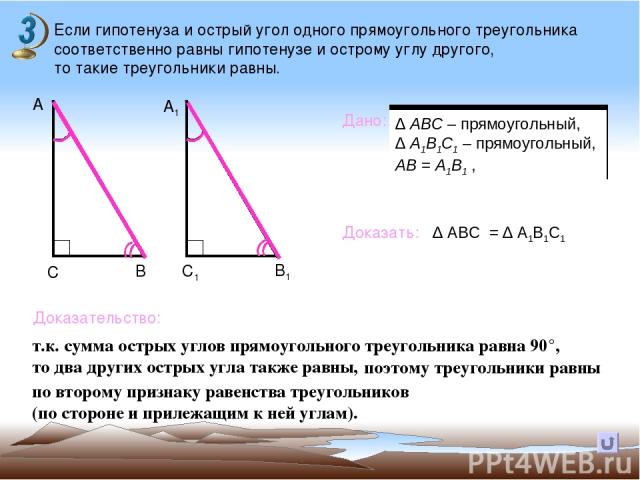
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого, то такие треугольники равны. В А А1 С С1 В1 Дано: Доказать: Доказательство: т.к. сумма острых углов прямоугольного треугольника равна 90°, то два других острых угла также равны, ∆ АВС = ∆ А1В1С1

Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого, то такие треугольники равны. В А А1 С С1 В1 Дано: Доказать: Доказательство: ∆ АВС = ∆ А1В1С1 Наложим ∆ А1В1С1 на треугольник ∆ АВС. Т.к. АС = А1С1 и АВ = А1В1, то они при наложении совпадут. Тогда вершина А1 совместиться с вершиной А. Но и тогда и вершины В1 и В также совместятся. Следовательно, треугольники равны.

Домашнее задание Учебник Бурда стр.118-120 – признаки равенства прямоугольных треугольников выучить. Стр. 123 №21 Учебник Бевз стр. 110-111 – признаки выучить стр.119 №446,448,457

Желаю удачи в изучении геометрии