Презентация на тему: Пределы функций

Математический анализ Составитель: Никулина Л.С., старший преподаватель кафедры Математики и Моделирования

Введение

Назначение курса Математический анализ является фундаментальной дисциплиной, составляющей основу математического образования. Курс предназначен для ознакомления студентов с основными понятиями математического анализа и их применением к решению задач. В курсе излагаются традиционные классические методы математического анализа

Цели преподавания дисциплины Развитие интеллекта и способностей к логическому и алгоритмическому мышлению; Обучение основным математическим методам, необходимым для анализа и моделирования технических и других задач.

Задачи преподавания На примерах продемонстрировать студентам сущность математических методов, научить приемам исследования и решения математически формализованных простейших задач, привить навыки самостоятельной работы с математической литературой.

Литература Основная литература: Л. Д. Кудрявцев. Курс математического анализа, т. 1, 2.- М.: высшая школа, 1981 Г. Н. Берман. Сборник задач по курсу математического анализа. – М.: Наука, 1987. Н. С. Пискунов. Дифференциальное и интегральное исчисления, т. 1, 2. - М.: Наука, 1984.

Литература Дополнительная литература: Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики.-М.: Наука, 1978. Учебно-методические разработки: Л. Я. Дубинина, Л. С. Никулина, И. В. Пивоварова. Курс лекций по высшей математике, ч. 1, 2.-Владивосток, изд. ВГУЭиС, 2001. Сборник задач по высшей математике. Сост. И. В. Пивоварова, Л. Я. Дубинина, Л. С. Никулина. -Владивосток, изд. ВГУЭиС, 2002.

Контроль Виды контроля: В процессе обучения студенты должны выполнить 2 контрольных работы, 3 ИДЗ и сдать теорию. Кроме того, студенты должны пройти промежуточную аттестацию. Итоговая аттестация предусмотрена в виде экзамена (компьютерное тестирование).

Аттестации Способы проведения промежуточных аттестаций, способ проведения итоговой аттестации и условия получения на ней положительной оценки. Для получения положительной оценки на экзамене студент должен выполнить все контрольные работы, выполнить и защитить все ИДЗ, проявлять активность на занятиях и регулярно выполнять все домашние задания.

Пределы и непрерывность 1. Определение предела функции. 2. Односторонние пределы. 3. Бесконечно малые и бесконечно большие. 4. Теоремы о пределах. 5. Некоторые признаки существования предела. 6. Замечательные пределы. 7. Непрерывность. 8. Свойства непрерывных функций.

Лекция 1

Пределы функций

Определение функции Если каждому элементу х Х поставлен в соответствие единственный элемент у=f(х) У ,где Х и Y -данные числовые множества, и при этом каждому элементу у У поставлен в соответствие хотя бы один элемент х Х, то у называется функцией от х, определенной на множестве Х.

Обратная функция Пусть между элементами множеств X и Y функция y=f(x) устанавливает взаимно однозначное соответствие, то есть x X соответствует один и только один его образ y =f(x) Y и обратно, для y Y найдется единственный прообраз x X такой, что f(x) = y. Тогда функция ,где y Y, устанавливающая соответствие между элементами множеств Y и X, называется обратной для функции y = f(x).

Определение окрестности Окрестностью О (а) точки а называется любой интервал x , окружающий эту точку, из которого, как правило, удалена сама точка а. Под окрестностью О( ) символа бесконечность понимается внешность любого отрезка , , то есть О ( ) = (- , ) ( ,+ ).

Определение предельной точки δ-окрестностью точки а называется интервал (а–δ,а+δ), не содержащий точку а, т.е. О (а, δ) = (а- δ, а) (а, а + δ). Пусть функция f(x) определена на множестве X, кроме быть может точки а.

Точку а мы будем называть предельной точкой множества X, если в любой δ -окрестности точки а содержится бесконечно много точек x X, то есть О (а)∩X для О(а).

Определение предела Число А называется пределом функции f(x) в точке а (или при x а), если для любого 0 существует число δ( ) 0 такое, что для любого x X, удовлетворяющего условию 0 x – а δ, следует неравенство f (x) – A .

Другое определение предела Говорят, что число А является пределом функции f(x) при x а, если для 0 существует δ-окрестность точки а О (а,δ) = {x| 0< |x-a|<δ},где δ =δ ( ), такая, что для x O (а, δ) выполняется неравенство f(x) – A . При этом пишут:

Утверждение эквивалентно следующему: f(x) – A при x ∆, где ∆ = ∆( ) зависит от и по смыслу определения является достаточно большим положительным числом. Множество всех точек x, для которых x ∆, очевидно является симметричной окрестностью символа .

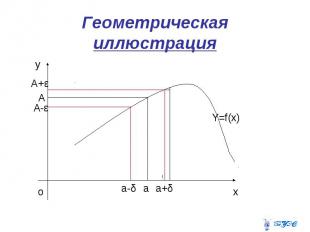
Геометрическая иллюстрация

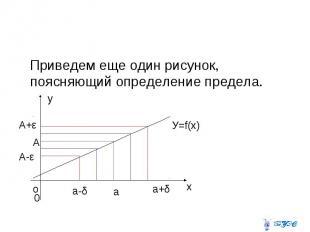
Приведем еще один рисунок, поясняющий определение предела.

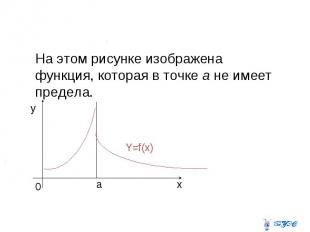
На этом рисунке изображена функция, которая в точке а не имеет предела.

Односторонние пределы

Односторонние пределы Любой интервал ( , а), правым концом которого является точка а, называется левой окрестностью точки а. Аналогично любой интервал (a, ), левым концом которого является точка а, называется ее правой окрестностью.

Односторонние пределы Символически запись означает, что х стремится к а справа, оставаясь большим а, то есть при х > а; запись означает, что х стремится к а слева, то есть при х < а.

Односторонние пределы будем называть левосторонним пределом функции (при слева), - это правосторонний предел функции.

Односторонние пределы Теорема о существовании предела Функция у = f(х) имеет в том и только том случае, когда существуют и равны друг другу ее левосторонний и правосторонний пределы при . Tогда = = =

Бесконечно малые и бесконечно большие

Функция (x) называется бесконечно малой при х а, если Ясно, что тогда (x) для всех x O(а, δ) и > 0. Например, функция является бесконечно малой при x 0.

Функция f(х) называется бесконечно большой при если . Это равносильно тому, что каким бы ни было число М > 0, найдется такая окрестность О (а, δ), что для всех x O (а, δ) M. Например, бесконечно большая при x 0 .

Лемма. Если f(х)→ при х→а, →0 при х а. Если (x) 0 при x a, то при x a и (x) 0.

Лекция 2

Свойства бесконечно малых. Теорема 1. Алгебраическая сумма конечного числа бесконечно малых при x а функций есть функция бесконечно малая при x а.

Теорема 2. Произведение конечного числа бесконечно малых при x a функций есть бесконечно малая при x a функция.

Теорема 3. Произведение бесконечно малой при x a функции на функцию, ограниченную при x a, есть бесконечно малая при x a.

Следствие. Целая положительная степень бесконечно малой при x a функции (x) есть бесконечно малая при x a.

Если , то в силу определения предела функции получаем: f(x)-A < при x O(а,δ), что означает, что f(x) – A является бесконечно малой при x a.

Тогда, полагая f(x)-A= (x), получим: f(x) = A + (x), где (x) 0 при x a. Таким образом, имеем: <=> f(x) = А+ (x), где (x)→ 0 при x a.

Теоремы о пределах

Теорема. Если функция f(х) = с постоянна в некоторой окрестности точки а, то Теорема. Если f(х) имеет предел при х→а, то этот предел единствен.

Функция f(х) называется ограниченной на данном множестве Х, если существует такое положительное число М, что |f(х)| М при всех х Х. Если такое число М не существует, то функция f(х) называется неограниченной

Лемма. Если функция f(х) имеет предел А при х→а, то она ограничена в некоторой окрестности точки х = а. Теорема. Пусть существует и пусть М < f(x) < N в некоторой окрестности точки x = a. Тогда М А N. Положительная функция не может иметь отрицательного предела.

Теорема 1. Если в точке а существуют пределы функций f(x) и g(x), то в этой точке существует и предел суммы f(x) g(x),причём .

Теорема 2. Если в точке а существуют пределы функций f (x) и g (x), то существует и предел произведения f(x) g(х), причем

Следствие. Постоянный множитель можно выносить за знак предела.

Теорема 3. Если в точке а существуют пределы функций f(х) и g (x) и при этом , то существует и предел частного , причем . .

Пример Найти . По теореме о пределе частного

Пример Найти Преобразуем данную функцию так, чтобы выделить в числителе и знаменателе множитель , на который и разделим далее числитель и знаменатель:

Пример Найти Преобразуем данную функцию, умножив числитель и знаменатель на

Пример Еще один пример. Вычислить Положим .

Признаки существования предела «Теорема о двух милиционерах»

Теорема (о промежуточной функции). Пусть в некоторой окрестности О (а) точки а функция f(x) заключена между двумя функциями и , имеющими одинаковый предел А при x a, то есть и Тогда функция f(x) имеет тот же предел:

Первый замечательный предел Теорема. Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице, то есть . Этот предел называют первым замечательным пределом.

Первый замечательный предел Это объясняется тем, что бесконечно малая дуга почти не успевает изменить свое направление, т.е. искривиться.

Второй замечательный предел Второй замечательный предел: или или

Примеры Вычислим =

Примеры Найти Полагая , получим: =

Сравнение бесконечно малых Две бесконечно малые при х→а функции (х) и (х) называются бесконечно малыми одинакового порядка, если k, где k 0 и конечно. При этом пишут: (х) =О( (х))

Две бесконечно малые при х→а функции (х) и (х) называются эквивалентными при х→а, если . Это записывают так: (x) (x) при x→a.

Бесконечно малая при х→а функция (х) называется функцией более высокого порядка по сравнению с функцией (х) при х→а, если . В этом случае пишут (х) = о ( (х)) при x→a.

Приведем некоторые замечательные примеры в дополнение к первому и второму замечательным пределам.

Теорема. Если при бесконечно малые , то Пример.