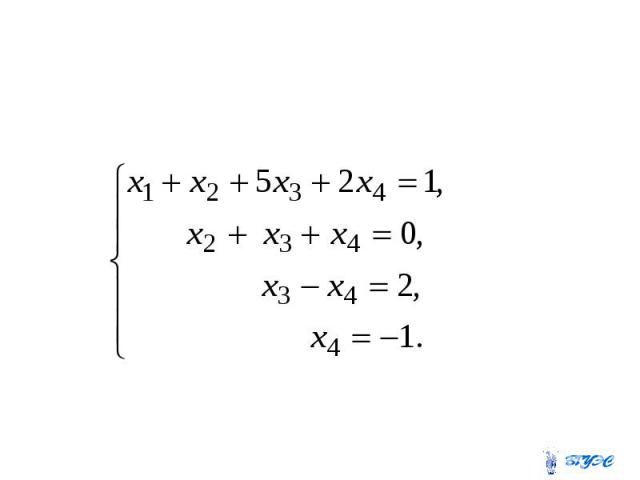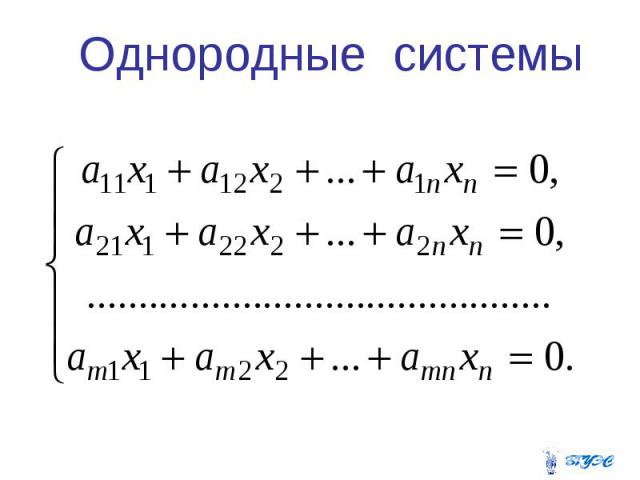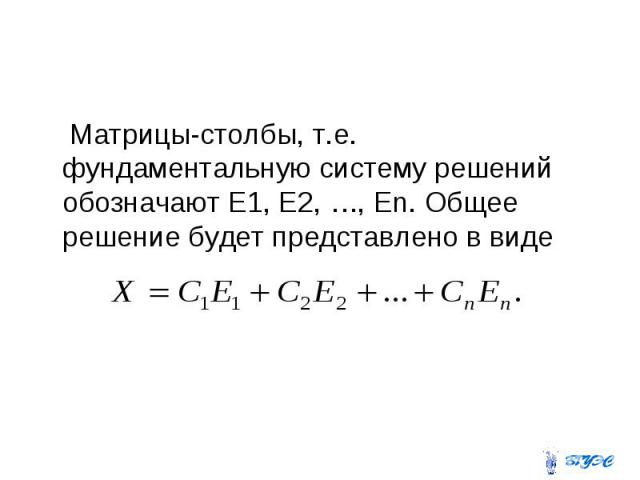Презентация на тему: Метод Гаусса решения систем линейных уравнений

Метод Гаусса решения систем линейных уравнений

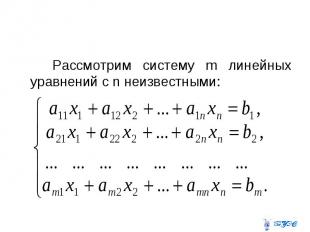
Рассмотрим систему m линейных уравнений с n неизвестными:

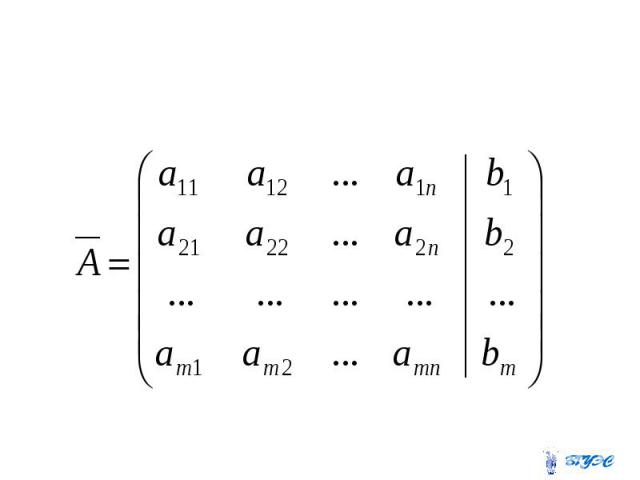
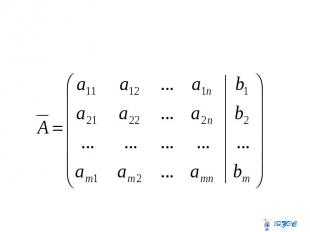
Назовем матрицей системы матрицу, составленную из коэффициентов при неизвестных. Матрицу, полученную из А добавлением столбца свободных членов, называют расширенной матрицей:

Теорема Кронекера–Капелли Для того чтобы система линейных уравнений была совместной, необходимо и достаточно, чтобы ранг матрицы системы был равен рангу ее расширенной матрицы, т.е.

Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение, если же ранг меньше числа неизвестных, то система имеет множество решений.

Две системы, множества решений Две системы, множества решений которых совпадают, называются эквивалентными или равносильными. Преобразование, применение которого превращает систему в новую систему, эквивалентную исходной, называется эквивалентным или равносильным преобразованием.

Пример Исследовать систему линейных уравнений

Составим расширенную матрицу системы и с помощью элементарных преобразований вычислим одновременно ранги обеих матриц.

Метод Гаусса Для того чтобы решить систему уравнений методом Гаусса выписывают расширенную матрицу этой системы и над строками этой матрицы производят элементарные преобразования, приводя ее к виду, когда ниже главной диагонали, содержащей элементы будут располагаться нули.

Разрешается: 1) изменять порядок строк матрицы, что соответствует изменению порядка уравнений; 2) умножать строки на любые отличные от нуля числа, что соответствует умножению соответствующих уравнений на эти числа; 3) прибавлять к любой строке матрицы другую, умноженную на отличное от нуля число, что соответствует прибавлению к одному уравнению системы другого, умноженного на число.

С помощью этих преобразований каждый раз получается расширенная матрица новой системы, равносильной исходной, т. е. такой системы, решение которой совпадает с решением исходной системы

Установить совместность и решить систему

Выпишем расширенную матрицу системы и поменяем местами первую и вторую строки для того, чтобы элемент равнялся единице (так удобнее производить преобразования матрицы).

Прямой ход

Обратный ход Ранги матрицы системы и ее расширенной матрицы совпали с числом неизвестных. Согласно теореме Кронекера-Капелли система уравнений совместна и решение ее единственно. Выпишем систему уравнений, расширенную матрицу которой мы получили в результате преобразований:

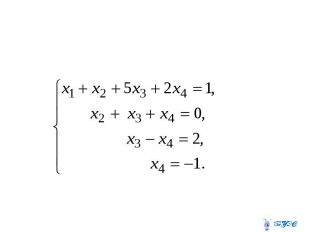
Имеем Далее, подставляя его в третье уравнение, найдем Подставляя и во второе уравнение, получим и, наконец, подставляя в первое уравнение найденные неизвестные, получим Таким образом, имеем решение системы

Общее решение системы линейных уравнений Если ранг матрицы равен , то любой отличный от нуля минор порядка этой матрицы называется базисным.

Пример Решить систему уравнений

Выпишем расширенную матрицу системы и преобразуем ее

Однородные системы

Теорема о совместности однородной системы Для того чтобы однородная система линейных уравнений имела нетривиальное решение, необходимо и достаточно, чтобы ранг матрицы этой системы был меньше числа неизвестных n.

При r<n система является неопределенной, т.е. имеет бесчисленное множество решений, в том числе и нетривиальное. Если m=n, т.е. число уравнений совпадает с числом неизвестных, матрица системы является квадратной. условие r<n в этом случае означает, что определитель системы, т.е. det А=0, что следует из определения ранга матрицы.

Пример

Составим матрицу системы и методом элементарных преобразований найдем ее ранг.

r=2.

Выберем в качестве базисного минор Тогда укороченная система имеет вид

Общее решение системы

Фундаментальная система решений Назовем фундаментальной системой решений систему матриц-столбцов, полученную из общего решения при условии, что свободным неизвестным дают последовательно значения

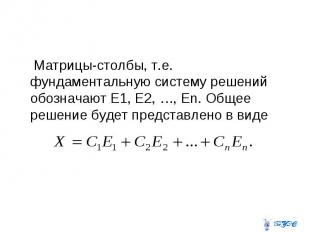
Матрицы-столбы, т.е. фундаментальную систему решений обозначают Е1, Е2, …, Еn. Общее решение будет представлено в виде

Из общего решения последней системы найдем фундаментальную систему решений. , Общее решение можно записать в виде