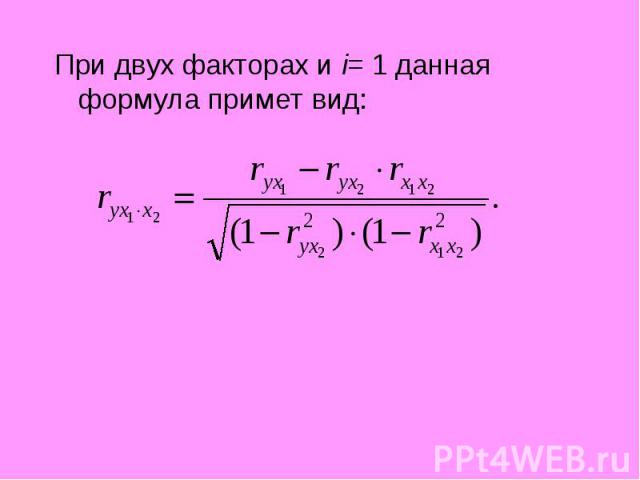Презентация на тему: Множественная регрессия и корреляция (продолжение)

Лекция № 6 множественная регрессия и корреляция. (продолжение)

При исключении из регрессии р+1 фактора коэффициент детерминации должен уменьшаться, а остаточная дисперсия возрастать; При исключении из регрессии р+1 фактора коэффициент детерминации должен уменьшаться, а остаточная дисперсия возрастать; и

Выбор формы уравнения регрессии. Как и в парной зависимости, возможны разные виды уравнений множественной регрессии: линейные и нелинейные. наиболее широко используются линейная и степенная функции .

В линейной множественной регрессии В линейной множественной регрессии параметры при переменной x называются коэффициентами «чистой» регрессии. Они характеризуют среднее изменение результата с изменением соответствующего фактора на единицу при неизменном значении других факторов, закрепленном на среднем уровне.

Возможен и иной подход к построению уравнения множественной регрессии ,когда на основе матрицы коэффициентов корреляции строится уравнение регрессии в стандартизованном виде: Возможен и иной подход к построению уравнения множественной регрессии ,когда на основе матрицы коэффициентов корреляции строится уравнение регрессии в стандартизованном виде:

Где -стандартизованные переменные Где -стандартизованные переменные Для которых среднее значение равно нулю а среднее квадратическое отклонение равно единице: -стандартизованные коэффициенты регрессии.

Стандартизованные коэффициенты регрессии показывают, на сколько % изменится в среднем результат, если соответствующий фактор xi изменится на 1 % при неизменном среднем уровне других факторов. Стандартизованные коэффициенты регрессии показывают, на сколько % изменится в среднем результат, если соответствующий фактор xi изменится на 1 % при неизменном среднем уровне других факторов.

Стандартизованные коэффициенты регрессии i сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. Стандартизованные коэффициенты регрессии i сравнимы между собой. Сравнивая их друг с другом, можно ранжировать факторы по силе их воздействия на результат. В этом основное стандартизованных коэффициентов регрессии в отличие от коэффициентов “чистой ” регрессии, которые несравнимы между собой.

коэффициенты “чистой ” регрессии связанны со стандартизованными коэффициентами регрессии следующими формулами : коэффициенты “чистой ” регрессии связанны со стандартизованными коэффициентами регрессии следующими формулами : Это позволяет от уравнения регрессии в стандартизованном виде переходить к уравнению регрессии в естественном виде.

Пример. Пусть функция издержек производства y(тыс. руб.) характеризуется уравнением вида Пример. Пусть функция издержек производства y(тыс. руб.) характеризуется уравнением вида x1 - основные производственные фонды(тыс.руб.) х2 - численность занятых в производстве(чел.)

Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс.руб. влечет за собой увеличение затрат в среднем на 1,2 тыс.руб. , а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс.руб. Анализируя его, мы видим, что при той же занятости дополнительный рост стоимости основных производственных фондов на 1 тыс.руб. влечет за собой увеличение затрат в среднем на 1,2 тыс.руб. , а увеличение численности занятых на одного человека способствует при той же технической оснащенности предприятий росту затрат в среднем на 1,1 тыс.руб. Однако это не означает ,что фактор x1 оказывает более сильное влияние на издержки производства по сравнению с фактором x2.

уравнение регрессии в стандартизованном виде выглядит так уравнение регрессии в стандартизованном виде выглядит так Вывод:

Так как < (0,5<0,8) ,то можно заключить ,что большее влияние оказывает на производство продукции фактор , а не , как кажется из уравнения регрессии в натуральном виде . Так как < (0,5<0,8) ,то можно заключить ,что большее влияние оказывает на производство продукции фактор , а не , как кажется из уравнения регрессии в натуральном виде .

Рассмотренный смысл стандартизованных коэффициентов регрессии позволяет их использовать при отсеве факторов –из модели исключаются факторы с наименьшим значением .

Индекс множественной корреляции Оценивает тесноту совместного влияния факторов на результат ( 0 ; 1 ) Значение должно быть больше или равно максимальному парному индексу корреляции

ЧАСТНАЯ КОРРЕЛЯЦИЯ Частные коэффициенты (или индексы) корреляции характеризуют тесноту связи между результатом и соответствующим фактором при неизменном уровне других факторов, включенных в уравнение регрессии (-1;1)

частные показатели корреляции широко используются при частные показатели корреляции широко используются при 1) решении проблемы отбора факторов. 2) ранжировании факторов, участвующих в множественной регрессии – для линейных связей (при нелинейной взаимосвязи исследуемых признаков эту функцию выполняют частные индексы детерминации ).

Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Порядок частного коэффициента корреляции определяется количеством факторов, влияние которых исключается. Например, — коэффициент частной корреляции первого порядка.

Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле Коэффициенты частной корреляции более высоких порядков можно определить через коэффициенты частной корреляции более низких порядков по рекуррентной формуле

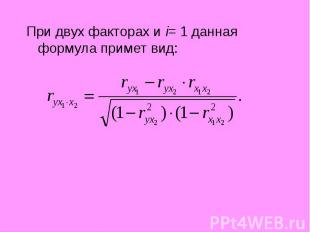
При двух факторах и i= 1 данная формула примет вид: При двух факторах и i= 1 данная формула примет вид:

Соответственно при i = 2 и двух факторах частный коэффициент корреляции у с фактором х2 можно определить по формуле Соответственно при i = 2 и двух факторах частный коэффициент корреляции у с фактором х2 можно определить по формуле