Презентация на тему: Неравенства и их решения

Неравенства и их решения

Неравенство Решить неравенство.Совокупность неравенств
Неравенства Алгебраические рациональные иррациональные Трансцендентные

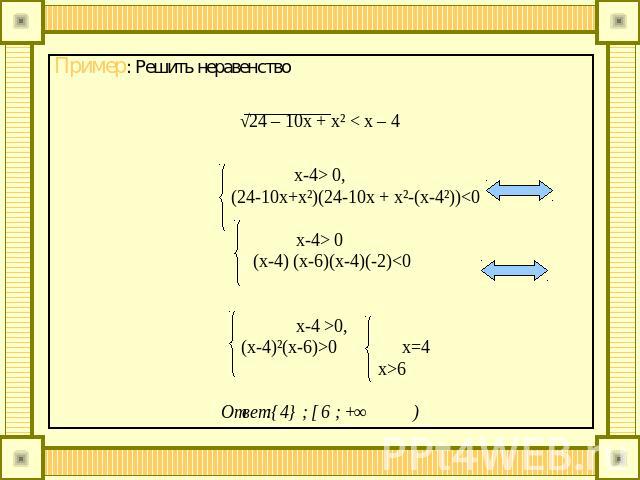
Пример: Решить неравенство√24 – 10x + x² < x – 4 x-4> 0, (24-10x+x²)(24-10x + x²-(x-4²))<0x-4> 0(x-4) (x-6)(x-4)(-2)<0 x-4 >0, (x-4)²(x-6)>0 x=4 x>6Ответ:{4} ; [ 6 ; +∞)

Методом интервалов: 1. Все члены неравенства переносятся в левую часть и приводятся к общему знаменателю.2. Определить критические точки.3. Критические точки наносятся на числовую прямую, прямая разбивается при этом на интервалы.4. Определить знаки на интервалах. 5. . Множество решений неравенств объединяется интервалом с соответствующим знаком, при этом случае , если неравенство нестрогое ,то к этому множеству прибавляется корни числителя.

Линейные неравенства– неравенства вида ax>b, ax< b, ax≥ b,ax ≤b , где a и b действительные числа или выражения , зависящие от параметров (ax – неизвестное)

Например, (3 - √10 )(2х- 7)< 0 6x- 21- 2x√10 + 7√10<0 36x² + 441+40x² + 490< 0 76x² + 931< 0 x² < 12.25x1= 3.5 x2= -3.5

(5 - a)x > a + 3a > 5, тогда х< a +3 5-a 2. а < 5, тогда x > a+3 5-a3. a =5 , x єØ

Квадратные неравенства – это неравенства вида ax² + b x +c > 0, где a, b, c – действительные числа

Если а>0 и D<0 ,то х єØЕсли a> 0 и D=0 , то x є( - ∞ ; -b/2a) (-b/2a ; + ∞ )Если а > 0 и D > 0, то х є(- ∞ ; х 1) (х 2; + ∞ ), где х1, х2- корни квадратного трехчлена.Если a< 0 D<0, то х є ØЕсли a<0 и D=0, то х є ØЕсли a<0 и D >0 , то х є (х 1;х 2), х 1, х 2 - корни квадратного трехчлена.

Пример: m x² – 2(m- 1)x + (m+2)1.Пусть m> 0 и D= (2-2m) ² - 4m(m +2)=1 – 12m < 0; нет решений2.Пусть m> 0 и D=0; m = ¼; уравнение имеет один корень. 3.Пусть m> 0 и D > 0, то есть mє (0; ¼ ). Тогда х (х 1; х2), где х 1 = 1/m[ (m – 1 - √1-4m), x 2 = 1/m (m-1+√1- 4m )4.Пусть m< 0 и D= 4(1- 4m)< 0; Тогда m є Ø5.Пусть m< 0 и D= 4(1-4m)> 0 m є Ø6.Пусть m< 0 и D= 4(1-4m)> 0, то есть m є ( - ∞ ;0) Тогда х є ( - ∞ ;х 1) (х 2; + ∞ )