Презентация на тему: Методы решения логарифмических уравнений

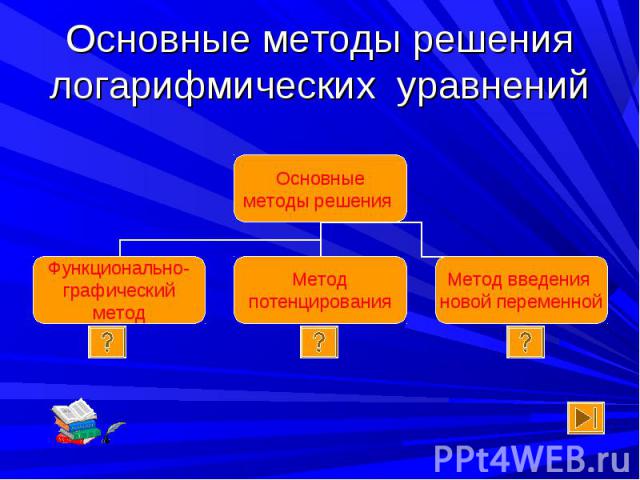
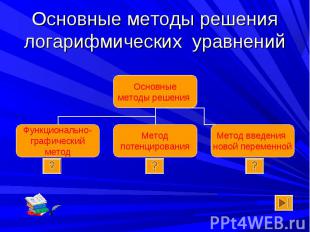
Определение Определение Логарифмическими уравнениями называют уравнения вида logа f (x) = logа g (x) , где а > 0, a ≠ 1, и уравнения, сводящиеся к этому виду.

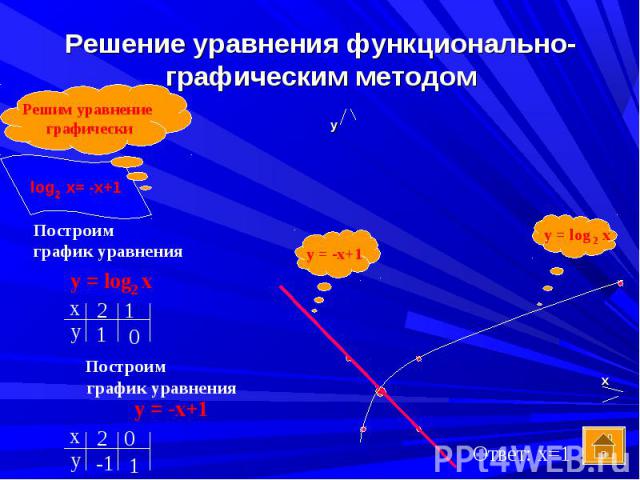
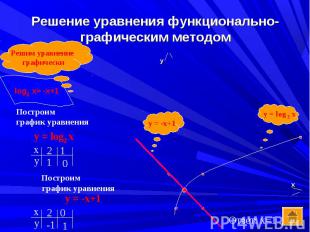
log2x = -x+1 log2x = -x+1 Ввести функцию f(x),равную левой части и g(x),равную правой части Построить на одной координатной плоскости графики функций y=f(x) и y=g(x) Определить точки пересечения графиков Найти абсциссы точек пересечения – это и есть корни уравнения Записать ответ

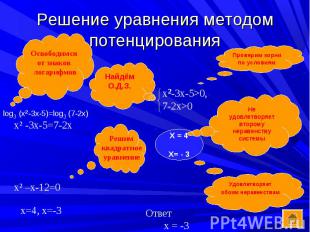
log3 (x²-3x-5)=log3 (7-2x) log3 (x²-3x-5)=log3 (7-2x) Записать условия, определяющие область допустимых значений (О.Д.З.): f (x)>0, g (x)>0 Перейти от уравнения logа f (x)=logа g (x) к уравнению f (x)=g (x) Решить полученное уравнение Проверить полученные корни по условиям, определяющим область допустимых значений переменной (О.Д.З.). Те корни уравнения, которые удовлетворяют этим условиям, являются корнями логарифмического уравнения. Те корни уравнения, которые не удовлетворяют хотя бы одному из этих условий, объявляются посторонними корнями логарифмического уравнения. Записать ответ

2log25x+5log5x+2=0 Ввести новую переменную, найти О.Д.З. Решить получившееся уравнение и найти значение новой переменной Сделать подстановку найденного значения новой переменной и вычислить неизвестную переменную Записать ответ

2а Рожь 2а Рожь 3а Солнце 1б Дети 1в Лошадь 3б Хлеб