Презентация на тему: Методы решения логарифмических уравнений 2

Ученицей 10 класса «б» Ученицей 10 класса «б» МБОУСОШ №1 г. Новочеркасска Пасенчук Анастасией под руководством учителя математики Филипповой Е.М.

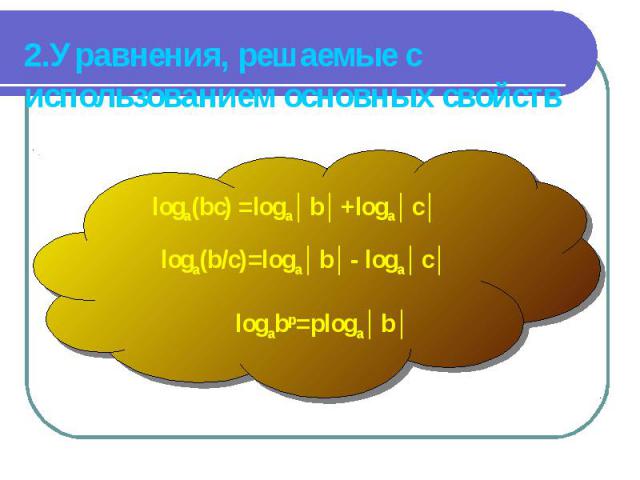
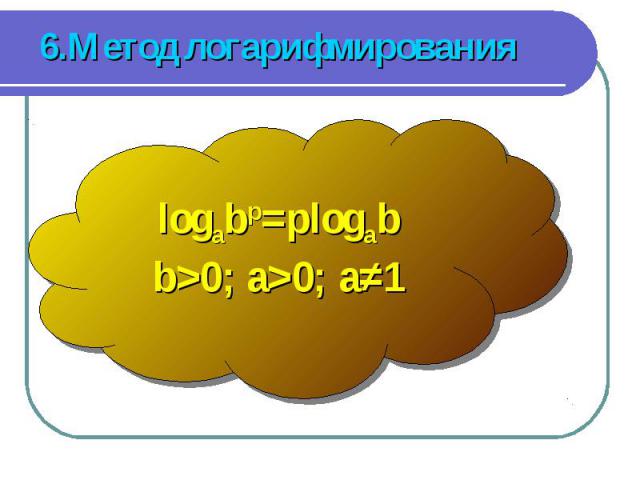
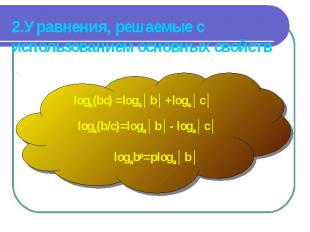
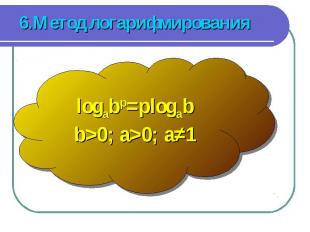
logab=c, ac =b, a>0, a≠1, b>0

log3(2-x)=2 ОДЗ: 2-x>0 log3(2-x)=2 ОДЗ: 2-x>0 2-x=32 x<2 2-x=9 -x=6 x=-6 Ответ: x=-6

log2(x+1)+log2(x+2)=1 ОДЗ: x+1>0 x>-1 log2(x+1)+log2(x+2)=1 ОДЗ: x+1>0 x>-1 log2(x+1)(x+2)=1 x+2>0 x>-2 (x+1)(x+2)=21 х>-1 x2+3x=0 x(x+3)=0 x1=0 x2=-3(не уд. ОДЗ) Ответ: x=0

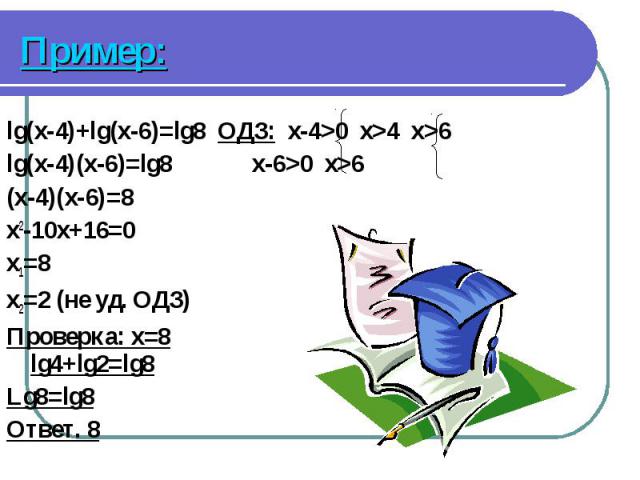
lg(x-4)+lg(x-6)=lg8 ОДЗ: x-4>0 x>4 x>6 lg(x-4)+lg(x-6)=lg8 ОДЗ: x-4>0 x>4 x>6 lg(x-4)(x-6)=lg8 x-6>0 x>6 (x-4)(x-6)=8 x2-10x+16=0 x1=8 x2=2 (не уд. ОДЗ) Проверка: x=8 lg4+lg2=lg8 Lg8=lg8 Ответ. 8

а)Уравнения, сводящиеся к квадратным а)Уравнения, сводящиеся к квадратным Пример1: lg2x-3lgx+2=0 ОДЗ: x>0 пусть lgx=t, tєR t2-3t+2=0 t1=1 t2=2 если t1=1, то если t2=2, то lgx=1 lgx=2 x=10 x=100 Ответ: x1=10, x2=100

Пример2: Пример2: lg2(10x)=5-lgx ОДЗ: x>0 (lg10+lgx)2=5-lgx 1+2lgx+lg2x-5+lgx=0 lg2x+3lgx-4=0 пусть lgx=t t2+3t-4=0 t1=1; t2= - 4 если t1=1, то если t2= - 4,то lgx=1 lgx=-4 x=10 x=0,0001 Ответ: x1=10, x2=0,0001

Пример: Пример: logx(9x2)log23x=4 ОДЗ: x>0 (logx9+logxx2)log23x=4 x≠1 (2logx3+2)log23x=4 (2/log3x+2)log23x=4 пусть log3x=t (2/t+2)t2=4 2t2+2t-4=0 t1=1; t2=-2 если t1=1, то если t2=-2, то log3x=1; x1=3; log3x=-2. x2=1/9. Ответ: x1=3, x2=1/9

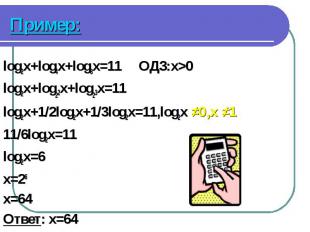
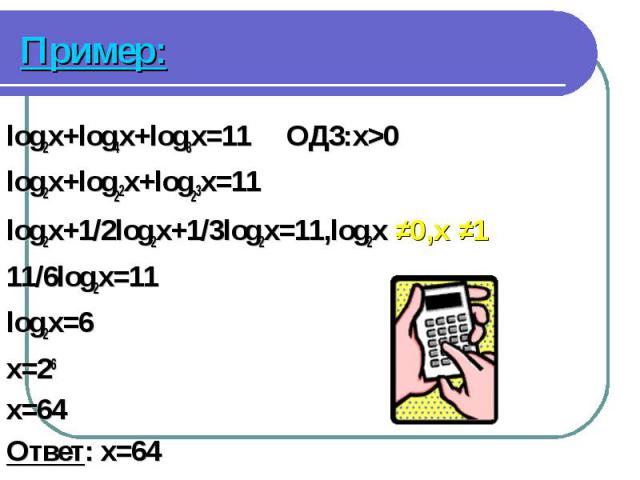
log2x+log4x+log8x=11 ОДЗ:x>0 log2x+log4x+log8x=11 ОДЗ:x>0 log2x+log22x+log23x=11 log2x+1/2log2x+1/3log2x=11,log2x ≠0,x ≠1 11/6log2x=11 log2x=6 x=26 x=64 Ответ: x=64

x (lgx+5)/3 =105+lgx ОДЗ:x>0 x (lgx+5)/3 =105+lgx ОДЗ:x>0 прологарифмируем уравнение по основанию 10 lgx(lgx+5)/3=lg105+lgx ((lgx+5)/3)lgx=(5+lgx)lg10 1/3(lgx+5)lgx=5+lgx|*3 (lgx+5)lgx=15+3lgx lg2x+5lgx=15+3lgx lg2x+2lgx-15=0 пусть lgx=t t2+2t-15=0 t1=-5; t2=3 если t1=-5, то lgx=-5 если t2=3, то lgx=3 x1=0,00001 x2=1000 Ответ: x1=0,00001, x2=1000

3xlog52+2log5x=64 ОДЗ: x>0,x ≠1 3xlog52+2log5x=64 ОДЗ: x>0,x ≠1 3*2log5x+2log5x=64 4*2log5x=64 |:4 2log5x=16 2log5x=24 log5x=4 x=54 x=625 Ответ: x=625

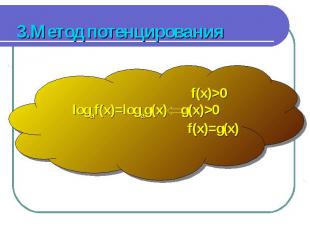
Пример: Пример: log3(x+1)+log4(5x+6)=3 ОДЗ: x> -1,2 y= log3(x+1) - возрастающая функция y= log4(5x+6)- возрастающая функция 3 - const Сумма двух возрастающих функций равна возрастающей функции. Используем утверждение: если возр. функция равна const или убыв. функции, тогда уравнение имеет один корень, который находится с помощью метода подбора. Ответ: x=2

Пример: Пример: log2(17-|sin0,5πx|)=√2x+15-x2 , x ≥0 1)рассмотрим левую часть т.к. 0≤ |sin0,5πx| ≥ 1 ,то log2(17-|sin0,5πx|) ≥log2(17-1)=log216=4 т.е. 0≤ |sin0,5πx| ≥ 4 при x=1 - достигается равенство 2)рассмотрим правую часть √2x+15-x2= √16-(x+1) ≤ √16=4=16-(x-1)2 √2x+15-x2≤4 при x=1 – достигается равенство Ответ: x=1

3log22(x+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0 3log22(x+1)-4log2(2x+1)log2(x+1)+log22(2x+1)=0 Делим на log22(2x+1) ОДЗ: x>1/2 3(log2(x+1)/log2(2x+1))2-4log2(2x+1)log2(x+1)/log22(2x+1)+1=0 t 3t2-4t+1=0 t1=1 t2=1/3 если t1=1 то, если t2=1/3 то, log2(x+1)/log2(2x+1)=1 log2(x+1)/log2(2x+1)=1/3 log2(x+1)=log2(2x+1) 3log2(x+1)=log2(2x+1) x+1=2x+1 log2(x+1)3=2x+1 x=0 x(x2+3x+1)=0 x1=0 x2=(-3+√5)/2 x3=(-3-√5)/2 Ответ: x1=0, x2= =(-3+√5)/2 не уд.

Пример: Пример: x√x=√xx ОДЗ: x>0, logx x√x =logx √xx x≠ 1 logx xx0,5 =logx (x0,5)x √xlogx x=0,5logxx √x=0,5x √x(1-0,5√x)=0 √x=0 (не уд.ОДЗ) (1-0,5√x)=0 √x=2 x=4 Ответ: x=4

(х – 1) = log2x (х – 1) = log2x Строим графики функций у = (х – 1) и у = log2x. Ответ: х = 1, х=2.

lq(х²-2х)=lg30-1; lq(х²-2х)=lg30-1; lg(x²+2x-3)=lg(6X-2); log3X*lоg2х =4 log32; log3X+log9X+log27X=1/12; log5(X-l0)-log5(X+2)=-1; 3+ 2logX+13=2log3(X+1).