Презентация на тему: Логарифмическая функция, её свойства и график

Физики шутят: “ Математика – царица всех наук, но служанка физики”. Так пошутить могут и музыканты, и биологи, и психологи и др. А это еще раз подтверждает правильность слов Карла Маркса “ Наука только тогда достигает совершенства, когда ей удается пользоваться математикой”.

***Дополнительное задание: остроумная алгебраическая головоломка, которой развлекались участники одного съезда физиков в Одессе. Некоторым учащимся на дом предлагалось творческое задание: число 3, целое и положительное, изобразить с помощью трех двоек и математических символов.            То есть любое целое положительное число можно изобразить с помощью трех двоек и математических символов.

Устная работа Вычисли log981= log416= log0.25= log91= log99= log 0.30.0081= log981=

Определение. Логарифмом положительно числа b по положительному и отличному от 1 основанию а называют показатель степени, в которую нужно возвести число а, чтобы получить число b.

Теорема об обратных функциях Если функция f(x) определена и монотонна на некотором промежутке X, причем D(f)=X, E(f)=Y, то существует обратная ей функция g(x), определенная на Y, т.е. D(g)=Y E(g)=X, причем, монотонность сохраняется. Графики взаимнообратных функций симметричны относительно прямой y=x

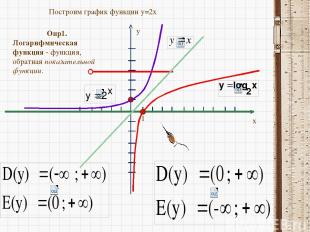
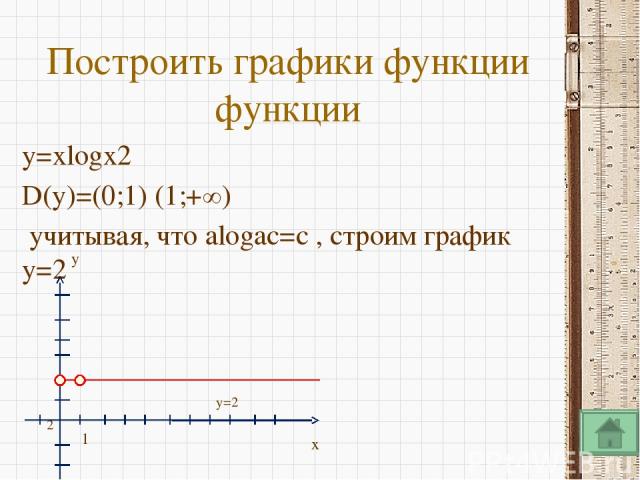
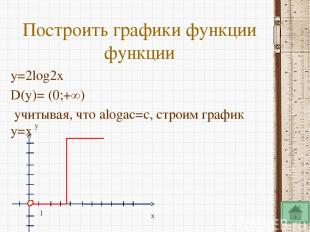
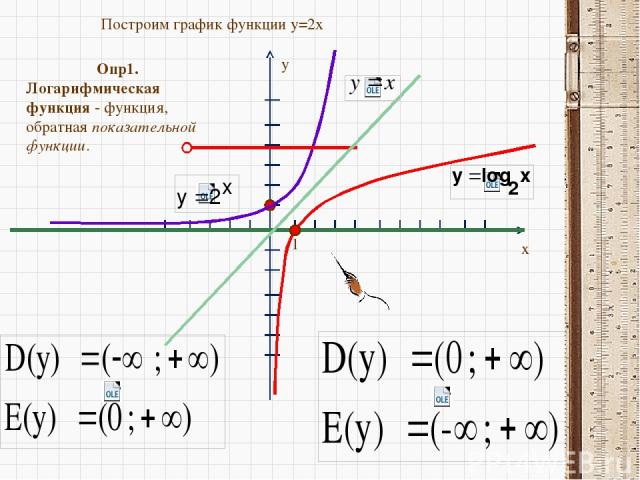
y x 1 Построим график функции y=2x Опр1. Логарифмическая функция - функция, обратная показательной функции.

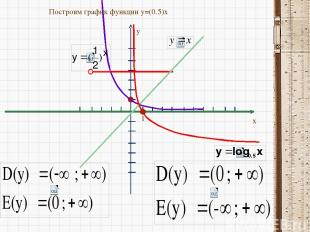
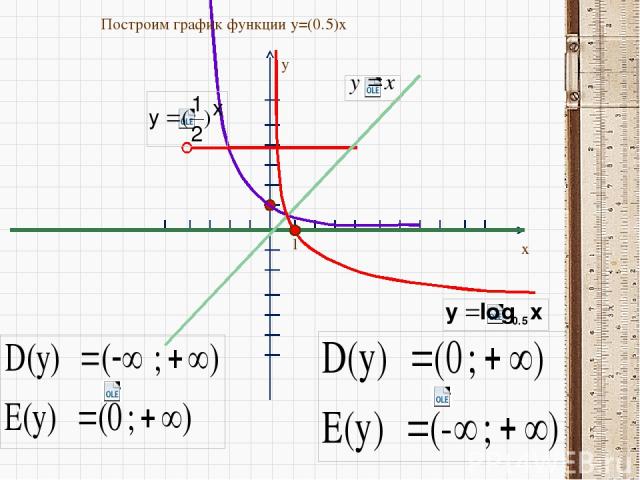
y x 1 Построим график функции y=(0.5)x

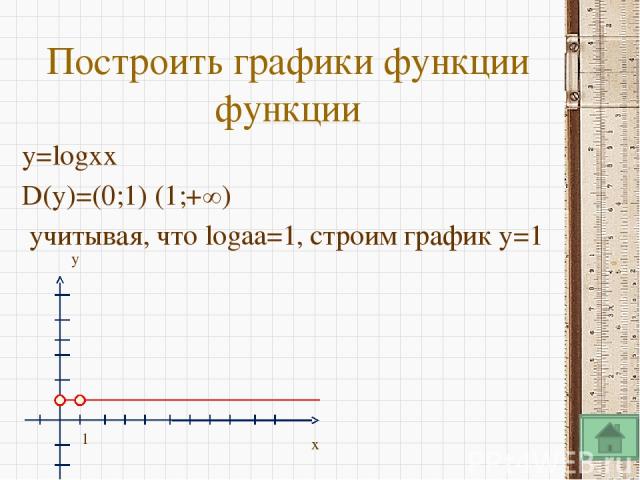
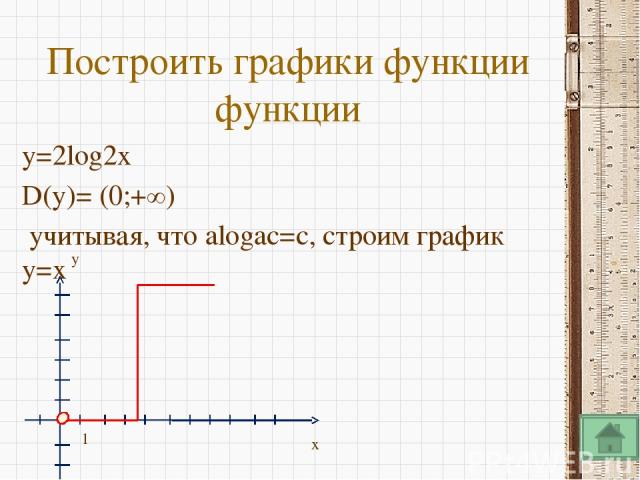
Опр.2 Функция вида   y = loga х (где а > 0, а ≠ 1)   называется логарифмической. 1) D(y):(0;+∞) Это следует из определения логарифма, так как выражение logax имеет смысл только при x > 0. Устная работа Найти D(y), если известно, что а > 0, а ≠ 1 а) y = loga х +1 б) y = loga (х+1) в) y = loga (1-x)

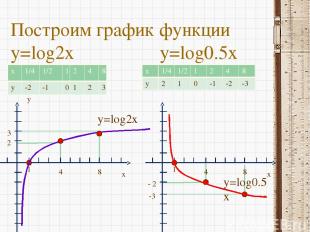
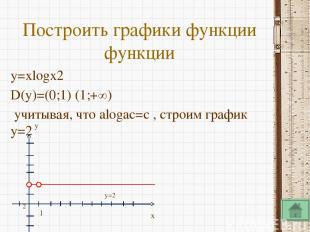
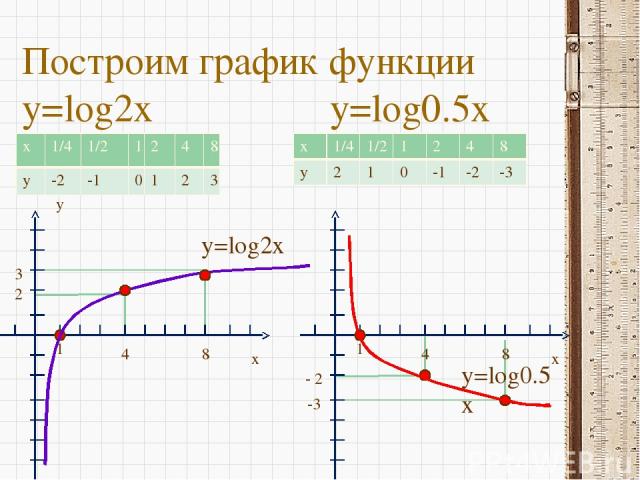
Построим график функции y=log2x y=log0.5x y x 1 4 8 2 3 y=log2x x 1 4 8 - 2 -3 y=log0.5x x 1/4 1/2 1 2 4 8 y 2 1 0 -1 -2 -3 x 1/4 1/2 1 2 4 8 y -2 -1 0 1 2 3

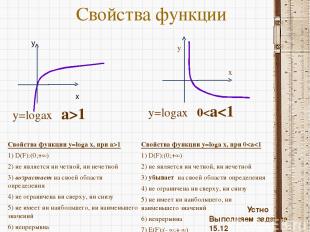
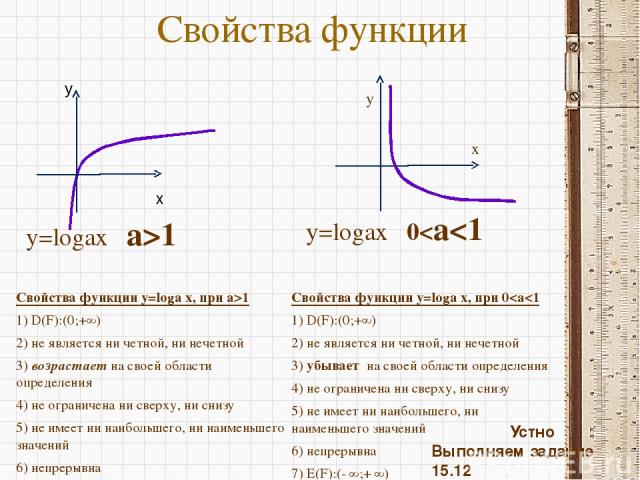
Свойства функции Свойства функции y=loga x, при a>1 1) D(F):(0;+∞) 2) не является ни четной, ни нечетной 3) возрастает на своей области определения 4) не ограничена ни сверху, ни снизу 5) не имеет ни наибольшего, ни наименьшего значений 6) непрерывна 7) E(F):(- ∞;+ ∞) 8) выпукла вверх Свойства функции y=loga x, при 0

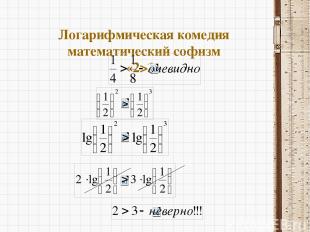
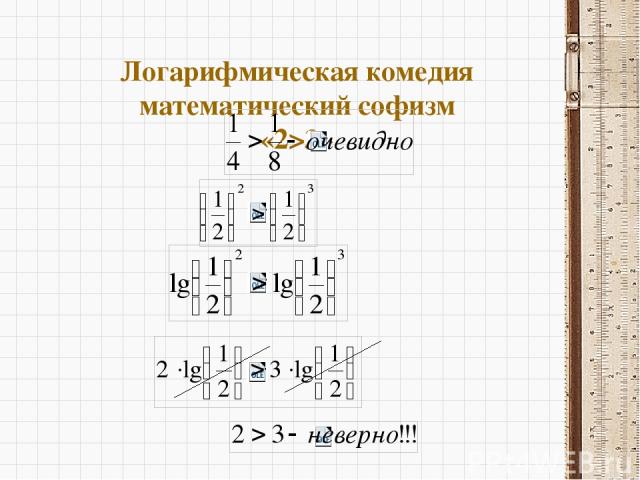
Логарифмическая комедия математический софизм «2>3»

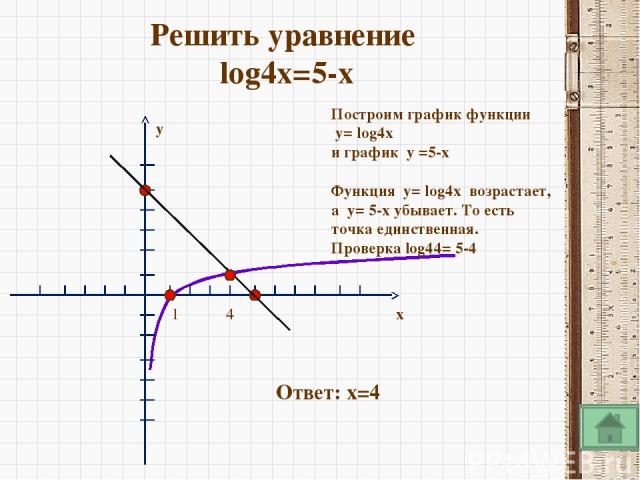
Работа в группах №1Найдите наибольшее и наименьшее значение функции на заданном промежутке y=lgx x€ [1;1000] №2 Решите уравнение и неравенства а) lоg4x=0; б) lоg4x>0 в) lоg4x

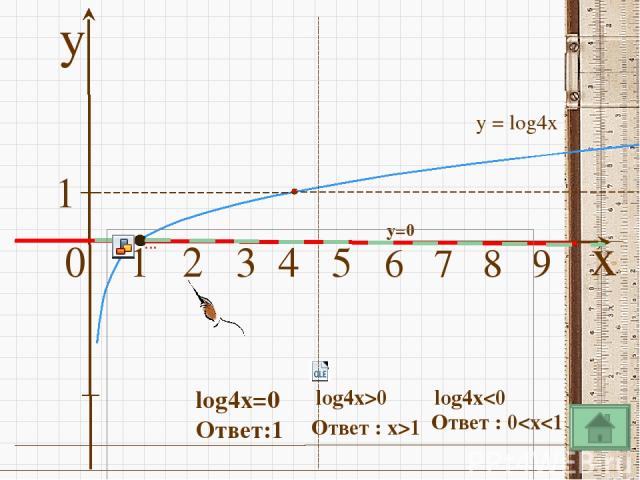
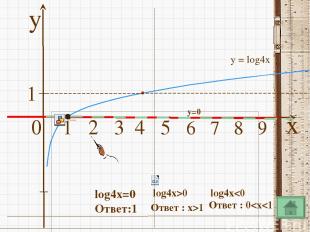
y 0 1 2 3 4 5 6 7 8 9 x 1 у = log4x y=0 lоg4x=0 Ответ:1 lоg4x>0 Ответ : x>1 lоg4x

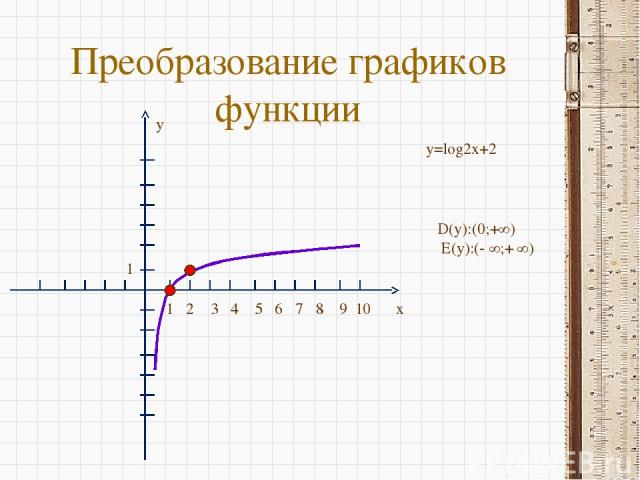
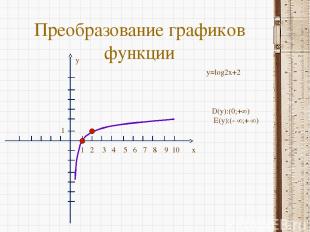
Преобразование графиков функции x y 1 2 3 4 5 6 7 8 9 10 1 y=log2x+2 D(y):(0;+∞) E(y):(- ∞;+ ∞)

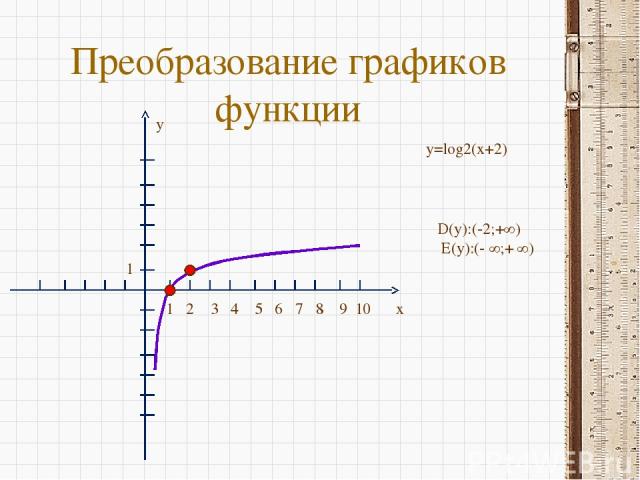
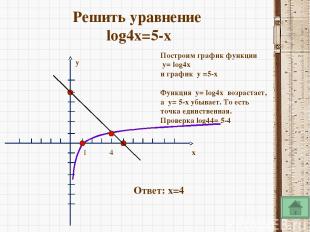
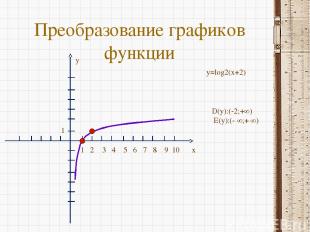
Преобразование графиков функции x y 1 2 3 4 5 6 7 8 9 10 1 y=log2(x+2) D(y):(-2;+∞) E(y):(- ∞;+ ∞)

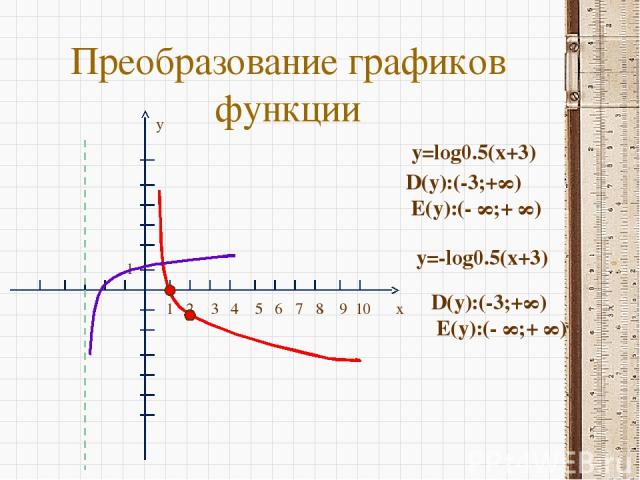
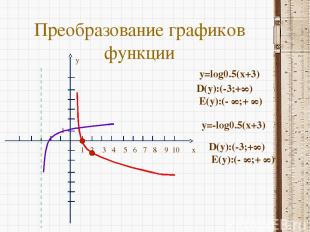
Преобразование графиков функции x y 1 2 3 4 5 6 7 8 9 10 1 y=log0.5(x+3) D(y):(-3;+∞) E(y):(- ∞;+ ∞) y=-log0.5(x+3) D(y):(-3;+∞) E(y):(- ∞;+ ∞)

Вычисления с помощью логарифма

Используемая литература: Задача на 2 слайде:http://www.bankrabot.com/part2/work_12766.html Учебник: Мордкович А.Г., «Алгебра и начала анализа», профильный уровень Задачник: Мордкович А.Г., «Алгебра и начала анализа», профильный уровень http://www.matica.info/material1.html -завещание Франклина.