Презентация на тему: Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители

Квадратный трехчлен. Квадратный трехчлен. Квадратичная функция. Квадратные уравнения. Разложение квадратного трехчлена на множители. (8 класс)

Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Разработано учителем математики МОУ «СОШ» п. Аджером Корткеросского района Республики Коми Мишариной Альбиной Геннадьевной

Содержание Квадратный трехчлен Квадратичная функция Квадратные уравнения Разложение квадратного трёхчлена на множители

КВАДРАТНЫЙ ТРЕХЧЛЕН

Определение Многочлен ax²+bx+c , где а, в, с – числа (коэффициенты), причем а ≠ 0 называется квадратным трехчленом Причем: а – старший коэффициент, в - второй коэффициент с – свободный член

Назовите коэффициенты: 1) 2х² - 6х + 1 2) - 2х² + 8х – 5 3) 3х² + 2х х² - 4х + 7 - х² - 8 6х² - х - 2

КВАДРАТИЧНАЯ ФУНКЦИЯ

Запомним Функция у = ax²+bx+c, где а, в, с – произвольные числа, причем а ≠0 называется квадратичной. Графиком квадратичной функции является парабола

Ветви параболы у = ax²+bx+c направлены вверх, если а > 0, и вниз если а < 0 Как найти координаты вершины параболы? – абсцисса х₀ вершины параболы вычисляется по формуле х₀ = - в/2а - ордината у₀ вершины параболы вычисляется подстановкой найденной х₀ в заданную функцию Осью симметрии параболы является прямая х = - в/2а

Найти координаты вершины параболы, её ось симметрии и построить её: у = 2х² - 8х + 1 у = - 2х² +16х – 5

Самостоятельно: вычислить координаты вершины параболы 1) у = х² + 4х + 5 2) у = 2х² + 4х 3) у = -3х² + 6х + 1 4) у = 3х² - 12х 5) у = х² + 6х - 2 6) у = -2х² + 8х - 5 7) у = -4х² - 8х

Рефлексия: 1) Сегодня на уроке я запомнил… 2) Сегодня на уроке я научился… 3) Сегодня на уроке я узнал … 4) Сегодня на уроке я выучил… 5) Сегодня на уроке было интересно … 6) Сегодня на уроке мне понравилось …

Квадратные уравнения

Содержание: Определение квадратного уравнения Классификация квадратных уравнений Способы решения квадратного уравнения

Определение Квадратным уравнением называется уравнение вида ax²+bx+c=0, где x - переменная, a, b, c – любые действительные числа, причем a≠0. (Почему?) Причем: а – старший коэффициент в - второй коэффициент с – свободный член

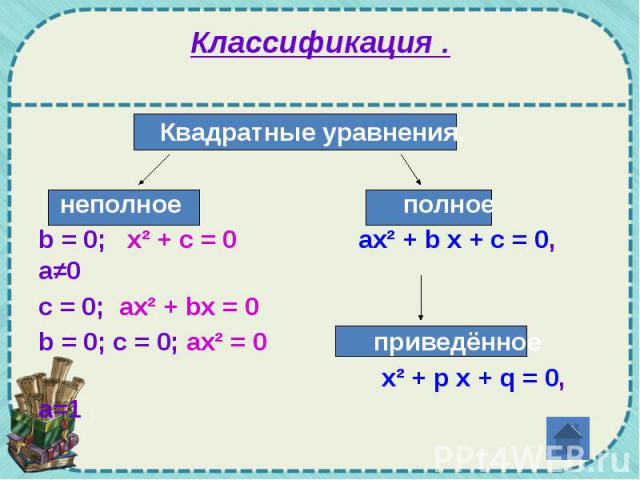
Классификация . Квадратные уравнения. неполное полное b = 0; x² + c = 0 ах² + b х + с = 0, а≠0 c = 0; ax² + bx = 0 b = 0; c = 0; ax² = 0 приведённое x² + p x + q = 0, а=1

Запомним Решить квадратное уравнение – это значит найти все его корни или установить, что их нет. Причем: квадратное уравнение может иметь либо 2 корня (если D >0), либо 1 корень (если D = 0), либо вообще не иметь корней (если D <0)

Способы решения квадратного уравнения: Разложением на множители Выделением полного квадрата По формуле корней (универсальный способ) По теореме Виета По коэффициентам Графический Введение новой переменной

Разложение левой части на множители

Выделение полного квадрата Например:

Рассмотрим ещё одно решение: Решим уравнение: х² + 6х - 7 = 0. Решение: х² + 6х -7 = 0. х² + 2 · 3 · х + 9 – 9 – 7 = 0 (х² + 6х + 9) - 9 – 7 = 0 (х +3)² – 16 = 0. (х +3)² = 16. Значит: х +3 = 4 и х + 3 = -4. х = 1 х =-7. Ответ: 1; -7.

Алгоритм решения квадратного уравнения ПО ФОРМУЛЕ КОРНЕЙ: Найти число, называемое дискриминантом квадратного уравнения и равное D = b²- 4ac. 2) Дискриминант показывает сколько корней имеет уравнение - если D<0, то данное квадратное уравнение не имеет корней;

- если D=0, то данное квадратное уравнение имеет единственный корень, который равен            - если D>0, то данное квадратное уравнение имеет два корня, которые равны

Решить уравнение: 2x2- 5x + 2 = 0 Здесь a = 2, b = -5, c = 2. Имеем D = b2- 4ac = (-5)2- 4 2 2 = 9. Так как D > 0, то уравнение имеет два корня. Найдем их по формуле то есть x₁ = 2 и x₂ = 0,5 - корни заданного уравнения.

Решить самостоятельно: x2- 2x + 1 = 0. 2x2- 3x +5= 0.

Работаем в парах: 1) Выберите квадратные уравнения и определите значения их коэффициентов: А) 2х² – 8 = 0; Б) -х² + 4х + 1 = 0; В) 3х³ + 2х – 9 = 0; Г) 5х – 3х² +2 = 0; Д) х – 3 = 0; Е) 3 – 5х² – х = 0; Ж) х² – х = 0. И) х² + 5 - 2х = 0 2) По коэффициентам указать приведенные уравнения. 3) Из квадратных уравнений выбрать неполные и решить их.

Проверим: Квадратные уравнения: А) 2х² – 8 = 0, где а=2; в=0; с=-8 Б) -х² + 4х + 1 = 0, где а=-1; в=4; с=1 Г) 5х – 3х² + 2 = 0, где а=-3; в=5; с=2 Е) 3 – 5х² – х = 0, где а=-5; в=-1; с=3 Ж) х² – х = 0, где а=1; в=-1; с=0 И) х² + 5 - 2х = 0, где а=1; в=-2; с=5

Проверим: 2) Приведенные квадратные уравнения: И) х² + 5 - 2х = 0 3) Неполные квадратные уравнения: А) 2х² – 8 = 0 и Ж) х² – х = 0 Решения: 2х² – 8 = 0 и х² – х = 0 2(х² - 4)=0 х(х-1)=0 2≠0; х² - 4 =0 х=0; х-1=0 х² = 4 х=0; х=1 х = ± 2

Пример решения квадратного уравнения Дано уравнение: Решение: Ответ:

Самостоятельная работа (по вариантам)

Проверь решение:

Проверь решение:

Запомни: по теореме Виета решаются только приведенные квадратные уравнения Теорема Виета: Если корни х₁ и х₂ приведённого квадратного уравнения х² + px + q = 0 , то х₁ + х₂ = - p, а х₁ · х₂ = q. Обратное утверждение: Если числа m и n таковы, что m + n = - p, m∙n = q, то эти числа являются корнями уравнения х² + px + q = 0. Обобщённая теорема: Числа х₁ и х₂ являются корнями приведённого квадратного уравнения х² + px + q = 0 тогда и только тогда, когда х₁ + х₂ = - p, х₁ · х₂ = q. Следствие: х² + px + q = (х – х₁)(х – х₂)

НАПРИМЕР Дано приведённое квадратное уравнение x²-7x+10=0 Решение: методом подбора проверим числа 2 и 5. Их произведение равно 10 (т.е. свободному члену уравнения), а их сумма равна 7, (т.е. второму коэффициенту уравнения , но с противоположным знаком ) Значит эти числа и являются корнями данного уравнения. Ответ: 2 и 5

Решить : Решаем вместе: 1) х² - 15х + 14 = 0 2) х² + 3х – 4 = 0 3) х² - 10х – 11 = 0 4) х² + 8х – 9 = 0

Проверим ответы: 1) х₁ =-1 х₂ =-7 2) х₁ = 1 х₂ = 18 3) х₁ =-1 х₂ =10 4) х₁ =-4 х₂ =-5

Решение квадратных уравнений по коэффициентам Если сумма коэффициентов равна 0, т.е. а + в + с = 0 , то х₁ = 1 х₂ = с/а. 2) Если а –в + с = 0, то х₁ = -1 х₂ = -с/а. 3) Если а = с, в = а ² + 1, то х₁ = –а = - с х₂ = -1/а = -1 /с. 4) Если а = с , в = - (а² + 1), то х₁ = а = с х₂ = 1/а = 1/с

Решить самостоятельно по группам: 1) 3х² + 4х + 1 = 0, 2) 5х² - 4х – 9 = 0, 3) 6х² + 37х + 6 = 0, 4) 7х² + 2х – 5 = 0, 5) 13х² - 18х + 5 = 0, 6) 5х² + х – 6 = 0, 7) 7х² - 50х + 7 = 0, 8) 6х² - 37х + 6 = 0, 9) 7х² + 50х + 7 = 0.

Проверим:

Проверим:

Проверим:

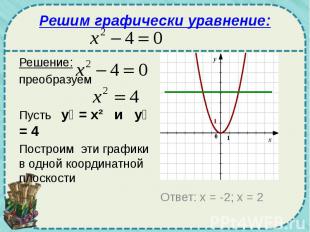
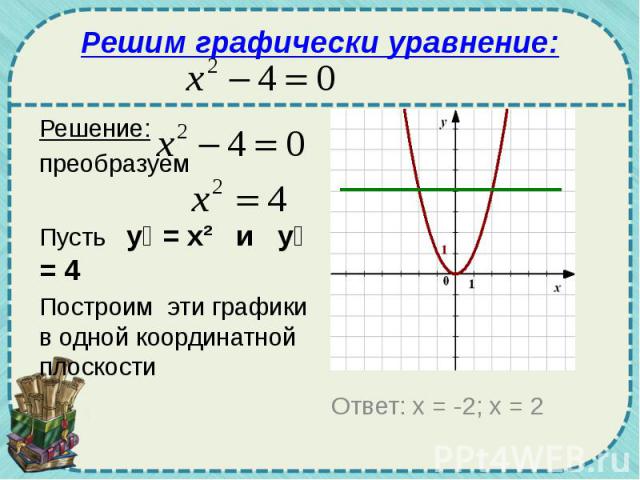
Решим графически уравнение: Решение: преобразуем Пусть у₁ = х² и у₂ = 4 Построим эти графики в одной координатной плоскости

Решить графически уравнения по вариантам: 1 вариант 1) х² + 2х – 3 = 0 2) - х² + 6х – 5 = 0 3) 2х² - 3х + 1 = 0

Введение новой переменной Умение удачно ввести новую переменную – облегчает решение Например: надо решить уравнение (2х+3)² = 3(2х+3) – 2. Решение: пусть: а = 2х + 3. Произведем замену переменной: а² = 3а - 2. Тогда получим уравнение а² - 3а + 2 = 0 и у него D > 0. Решим квадратное уравнение и получим: а₁ = 1, а₂ = 2. Произведем обратную замену и вернемся к переменной х: 1). если а₁ = 1, то 2х + 3 = 1 и тогда х₁ = - 1; 2). если а₂ = 2, то 2х + 3 = 2 и тогда х₂ = - 0,5 Ответ: -1; -0,5.

Решить самостоятельно в парах: а) (х² - х)² - 14(х² - х) + 24 = 0; б) (2х - 1)⁴ - (2х - 1)² - 12 = 0 Проверим ответы: а) б)

Разложение квадратного трехчлена на множители

Запомнить: Если квадратное уравнение ax²+bx+c=0 имеет корни х₁ и х₂, то квадратный трехчлен ax²+bx+c, раскладывается на множители следующим образом: ax²+bx+c= а·(х - х₁)(х - х₂).

Разложите квадратный трехчлен на множители: 1 вариант 1) х² - 11х + 24 2) х² + 7х + 12 3) - х² - 8х + 9 4) 3х² + 5х - 2 5) -5х² + 6х - 1

Проверим 1 вариант 1) (х-8)(х-3) 2) (х+3)(х+4) 3) – (х-1)(х+9) 4) 3·(х-1/6)(х+13/6) 5) -5·(х-1)(х- 0,2)

Рефлексия: Сегодня на уроке я запомнил… Сегодня на уроке я научился… Сегодня на уроке я узнал … Сегодня на уроке я выучил… Сегодня на уроке было интересно … Сегодня на уроке мне понравилось …

СПАСИБО ЗА УРОК !!!

Источники изображений http://www.avazun.ru/photoframes/&sort=&p=10 http://s59.radikal.ru/i163/0811/73/ad11fb505124.png