Презентация на тему: Квадратные уравнения

Квадратные уравнения

Автор: Бесфамильная Аннаученица 8-а классаРуководитель: Никифорова М.Н., учитель математикиГОУ СОШ №1968Москва2010г.

Цели проекта: Дать определение квадратного уравненияРассмотреть алгоритм решения квадратных уравненийПознакомить с историей решения квадратных уравненийИзучить теорему ВиетаНайти занимательный материал по данной теме(кроссворды, стихи)

Определение квадратного уравнения. Квадратным уравнением называется уравнение вида ах²+вх+с=0, где х – переменная, а,в,с – некоторые числа, причем а≠0.Числа а, в, с – коэффициенты квадратного уравнения. Число а – первый коэффициент, в – второй коэффициент, с – свободный член.Если в квадратном уравнении ах²+вх+с=0 хотя бы один из коэффициентов в или с равен нулю, то такое уравнение называется неполным квадратным уравнением.Квадратное уравнение, в котором коэффициент а=1 называется приведенным квадратным уравнением.

Стихотворение для запоминания формулы «Пэ», со знаком взяв обратным,На два мы его разделим.И от корня аккуратноЗнаком минут-плюс отделим.А под корнем, очень кстати,Половина «пэ» в квадрате,Минус «ку». И вот решеньеНебольшого уравненья.

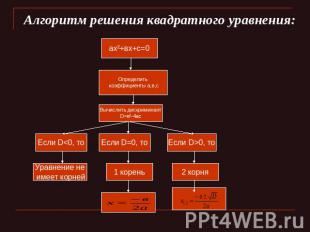
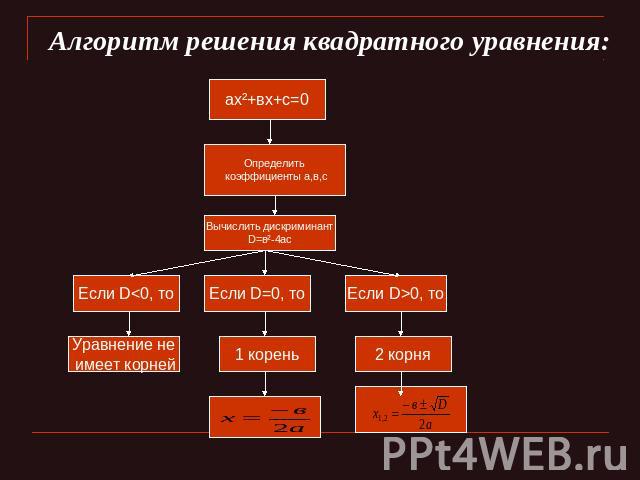
Алгоритм решения квадратного уравнения:

10. «Дискриминант» - по-латыни.11. Коэффициент с квадратного уравнения.12. Французский математик, который вывел формулы, выражающие зависимость корней уравнения от его коэффициентов. 1. Уравнение вида ах²+вх+с=о2.Квадратные уравнения, у которых первый коэффициент равен 1.3. Уравнения с одной переменной, имеющие одни и те же корни.4. Числа а,в и с в квадратном уравнении.5. Значение переменной, при котором уравнение обращается в верное равенство.6. Равенство, содержащее неизвестное.7. Неотрицательное значение квадратного корня.8. Древнегреческий математик, который нашел приемы решения квадратных уравнений без обращения к геометрии.9. Квадратное уравнение, в котором хотя бы один из коэффициентов в или с равен 0. Если вы разгадаете этот кроссворд верно, то сможете в выделенном вертикальном столбце прочитать термин, относящийся к теме.

Из истории решения квадратных уравнений. Уравнения 2-ой степени умели решать еще в Древнем Вавилоне во II тысячелетии до н.э. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид – при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактатахФормула корней квадратного уравнения «переоткрывалась» неоднократно. Один из первых дошедших до наших дней выводов этой формулы принадлежит индийскому математику Брахмагупте (около 598 г.). Среднеазиатский ученый ал-Хорезми (IX в.) в трактате «Китаб аль-джебр валь -мукабала» получил эту формулу методом выделения полного квадрата с помощью геометрической интерпретации.

Уравнение с вещественными коэффициентами Квадратное уравнение с вещественными коэффициентами a,b,c может иметь от 0 до 2 вещественных корней в зависимости от значения дискриминанта D = b2 − 4ac:

при D > 0 корней два, и они вычисляются по формуле при D = 0 корень один (в некоторых контекстах говорят также о двух равных или совпадающих корнях), кратности 2: при D < 0 вещественных корней нет. Существуют два комплексных корня, выражающиеся той же формулой (1) (без использования извлечения корня из отрицательного числа), либо формулой

для нахождения корней можно использовать эквивалентное выражение                              где k = b / 2. Это выражение является более удобным для практических вычислений при чётном b, то есть для уравнений вида ax² + 2kx + c = 0.

Квадратное уравнение вида x2 + px + q = 0, в котором старший коэффициент a равен единице, называют приведённым. В этом случае формула для корней

Мнемонические правила «Минус» напишем сначала,Рядом с ним p пополам,«Плюс-минус» знак радикала,С детства знакомого нам. Ну, а под корнем, приятель,сводится всё к пустяку:p пополам и в квадратеМинус несчастное прекрасное q.

Уравнение с комплексными коэффициентами В комплексном случае квадратное уравнение решается по той же формуле и указанным выше ее вариантам, но различимыми является только два случая: нулевого дискриминанта (один корень) и ненулевого (два корня).

По праву достойна в стихах быть воспетаО свойствах корней теорема Виета.Что лучше, скажи, постоянства такого:Умножишь ты корни - и дробь уж готова:В числителе с,  в знаменателе а,А сумма корней тоже дроби равна.Хоть с минусом дробь - это что за беда -В числителе в, в знаменателе а.  Теорема Виета

Теорема Виета Сумма корней приведённого квадратного уравнения x² + px + q = 0 равна коэффициенту p, взятому с обратным знаком, а произведение корней равно свободному члену q: В общем случае (для неприведённого квадратного уравнения ax² + bx + c = 0):

Разложение квадратного уравнения на множители Если известны оба корня квадратного уравнения, его можно разложить по формуле В случае нулевого дискриминанта это соотношение становится одним из вариантов формулы квадрата суммы или разности.

Уравнения, сводящиеся к квадратным является уравнением, сводящимся к квадратному. В общем случае оно решается заменой c последующим решением квадратного уравнения Также при решении можно обойтись без замены, решив совокупность двух уравнений Если f (x) = x², то уравнение принимает вид:ax^4 + bx² + c = 0Такое уравнение называется биквадратным

Выводы: 1 В процессе работы над презентацией я изучила решение квадратных уравнений.2 Научилась пользоваться формулами для решения квадратных уравнений 3 Узнала об истории решения 4 Данная презентация будет полезна учащимся 8-9классов для изучения и повторения при решении квадратных уравнений 5 Презентация окажет помощь учителям при объяснении темы «Квадратные уравнения»

Литература: 1. http://mathematic.su/teorema.html 2. http://megasoft2009.3dn.ru/load/27 3. http://www.rusedu.ru/ 4.http://ru.wikipedia.org/wiki/%D0%9A%D0%B2%D0%B0%D0%B4%D1%80%D0%B0%D1%82%D0%BD%D0%BE%D0%B5_%D1%83%D1%80%D0%B0%D0%B2%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5