Презентация на тему: Диофантовы уравнения

Диофантовы уравнения.

Цели и задачи.Определение диофантова уравненияБиография ДиофантаДиофантовые уравнения первой степениДиофантовые уравнения высших степенейПроект учащихся «Метод бесконечного спуска»Другие методы решения диофантовых уравнений

Образовательные:1.Познакомить учащихся с уравнениями, которые решаются в целых числах.2.Организовать самостоятельный поиск решений диофантовых уравнений.3.Рассмотреть различные приёмы решения.4.Научить решать текстовые задачи, по которым можно составить диофантово уравнение.Развивающие.1. Формирование умений обобщать, сравнивать, оценивать, контролировать, анализировать, делать выводы, 2. Развитие познавательных возможностей, творческих способностей, креативности личностных качеств,3.Организация способности общения (живого, виртуального, обоюдного, группового и т.д.),.4. Развитие инициативы, познавательного интереса,5. Обучение методам исследовательского поиска, 6. Развитие мыслительной деятельности,7.Развитие практической направленности изучаемого материала8. Привитие любви к математике

У мальчика было 50 р., на которые он хотел купить почтовые марки. В киоске имелись марки по 4 р. и по 3 р., но у киоскера совсем не было сдачи. Помогите мальчику и киоскеру выйти из создавшегося затруднения.

Решение.Пусть марок по 4 р. х штук, по 3 р. – у штук. Всего имеется 50 р., отсюда уравнение: 4 х + 3 у = 50 Эта задача имеет не одно, а несколько решений.

Первым начал рассматривать такие уравнения Диофант (II – III вв. до нашей эры). Он рассматривал уравнения, которые сегодня мы записали бы, например, так:ax + by = c; (1)где a, b и c целые числа, и ответ должен быть дан только в целых числах.Такие уравнения называют «диофантовыми».

Диофант пытался ответить на следующий вопрос: «Дано уравнение с целыми коэффициентами. Имеет ли оно целые решения?» Диофантовы уравнения - алгебраические уравнения или их системы с целыми коэффициентами, имеющие число неизвестных, превосходящее число уравнений, и у которых разыскиваются целые или рациональные решения. Примеры диофантовых уравнений: ax+by=c, x2+y2=d2.

Биографических данных о древнегреческом ученом-математике Диофанте из Александрии практически не сохранилось. До наших времен дошла лишь часть математического трактата Диофанта "Арифметика", 6 книг из 13, а также отрывки книги о многоугольных числах. В "Арифметике", Диофант излагал начала алгебры, привел множество задач, сводящихся к неопределенным уравнениям различных степеней, и отметил методы нахождения решений таких уравнений в рациональных положительных числах. Сочинения Диофанта были отправной точкой для теоретико-числовых исследований П. Ферма, Л. Эйлера, К. Гаусса и других математиков. Именем Диофанта названы два больших раздела теории чисел - теория диофантовых уравнений и теория диофантовых приближений.

Рассмотрим линейное диофантово уравнение 2х + 3у = 1. Найдите целые решения.Одно из решений – пара чисел х = 5, у = -3Проверка: 2 · 5 + 3 · (-3) = 1 Любое решение диофантова уравнения называется частным решением

При с = 0 уравнение (1) имеет вид ах + bу = 0и называется однородным диофантовым уравнением.Пример. 2х + 3у = 0 2х = -3уЛевая часть равенства делится на 2, а правая – на 3. Числа 2 и 3 взаимно просты. Поэтому у = 2n, x = -3n, где

В общем виде решением уравнения ах + bу = 0является пара (-b n, an)Общим решением диофантова уравнения 2х + 3у = 1 является х = 5 – 3n, y = -3 + 2n,

1 группа. Предложите как можно подобрать частное решение уравнения 31х + 11 у = 12 группа. Решите уравнение: 6х + 9у = 23 группа. Решите уравнение: 6х + 9у = 34 группа. Решите уравнение:2х + 3у = 7

Группа 1. Частное решение уравнения 31х + 11 у = 1 можно найти с помощью алгоритма Евклида: 31 11 22 2 11 9 9 1 9 2 8 4 1

Группа 2. 6х + 9у = 2(6х + 9у) ⫶ 3; 2 не делится на 3⟾ это уравнение не имеет решений. Группа 3. 6х + 9у = 3. Разделим обе части уравнения на 3. 2х + 3у = 1. Частное решение: х = 5; у = - 3. 2х + 3у = 2 ∙ 5 + 3 ∙ (-3)2 (х – 5) + 3 (у + 3) = 0. Сделаем замену:х´= х – 5, у´= у + 3; 2х´ + 3у´= 0; х´=-3n, у´=2nх = 5 + х´= 5 – 3n; у = -3 + у´= -3 + 2n. Ответ: (5 – 3n; -3 + 2n),

Группа 4. 2х + 3у = 7Частное решение х = 2; у = 1Решение соответствующего однородного уравнения: х = 3n; у = - 2n.Ответ: (2 + 3n; 1 - 2n),

Другой способ решения.2х + 3у = 7 х =

Диофантовы уравнения высших степеней. Задача 1.Доказать: что уравнение (x - y)3 + (y - z)3 + (z - x)3 = 30 не имеет решений в целых числах. Решение: Разложив левую часть на множители, приведем уравнение к виду (x - y)(y - z)(z - x) = 10. Заметим, что (x - y) + (y - z) + (z - x) = 0. С другой стороны, делителями 10 являются числа ±1, ±2, ±5, ±10. Нетрудно проверить, что сумма любых трех чисел из этого множества, дающих в произведении 10, не будет равняться 0.

Задача 2. Решите уравнение в целых числах : 3ху + 2х + 3у = 0 Решение:3ху + 2х + 3у + 2 = 23у (х + 1) + 2 (х + 1) = 2(3у + 2)(х + 1) = 2 3у + 2 = 2 х + 1 = 1 3у + 2 = 1 х + 1 = 2 3у + 2 = -2 х + 1 = - 1 3у + 2 = -1 х + 1 = -2 Решите системы и отберите целые решения

Проект учащихся «Метод бесконечного спуска»

2. Метод «бесконечного спуска»Предположим, что уравнение имеет решение, строим бесконечный процесс, в то время как по смыслу задачи этот процесс должен на чём-то закончиться. Часто метод бесконечного спуска применяется в более простой форме. Предположим, что мы уже добрались до естественного конца, и видим, что «остановиться» невозможно.

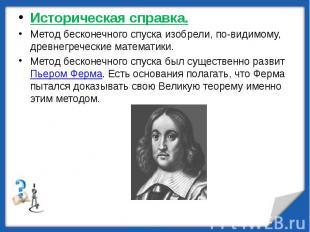
Историческая справка.Метод бесконечного спуска изобрели, по-видимому, древнегреческие математики. Метод бесконечного спуска был существенно развит Пьером Ферма. Есть основания полагать, что Ферма пытался доказывать свою Великую теорему именно этим методом.

Несмотря на отсутствие многих важных деталей в беглых заметках Ферма, в них отчетливо просматривался один из способов доказательства от противного, известный под названием метода бесконечного спуска. Чтобы доказать, что уравнение не допускает решения в целых числах, Ферма начал с предположения о существовании гипотетического решения в целых числах x = X1, y = Y1, z = Z1. При изучении свойств чисел (X1, Y1, Z1) Ферма показал, что если бы такое гипотетическое решение действительно существовало, то существовало бы меньшее решение (X2, Y2, Z2). Рассматривая это новое решение, Ферма смог показать, что если бы оно существовало, то существовало бы еще меньшее решение (X3, Y3, Z3) и т.д. Эйлер попытался воспользоваться методом бесконечного спуска в качестве исходного пункта при построении общего доказательства для всех других степеней в уравнении Ферма. Он хотел получить доказательство для всех вплоть до бесконечности, но прежде всего он хотел «опуститься на одну ступень» и получить доказательство при =3. В письме к прусскому математику Христиану Гольдбаху в августе 1753 года Эйлер сообщил, что ему удалось приспособить метод бесконечного спуска и успешно доказать Великую теорему Ферма для случая =3.

Задача.Решите уравнение в целых числах:

Значит числа х1, у1 и z1 – тоже делятся на 2. Сколько бы раз мы не делили на 2,получаем числа, которые снова делятся на 2. Таким свойством обладает только 0. Ответ: (0;0;0).

Задание для самостоятельной работы.Доказать, что уравнение x 3 + 2y 3 + 4z 3 - 6xyz = 0 в целых числах не имеет решений, не равных нулю одновременно.

Задача:Доказать, что уравнение x 3 + y 3 + z 3 = 2 имеет бесконечно много решений в целых числах. Решение: Положим x = a + b,   y = a - b. Тогда x 3 + y 3 = 2a 3 + 6ab 2. С учетом последнего равенства исходное уравнение принимает вид 2a 3 + 6ab 2 + z 3 = 2. Положив a = 1, получим z 3 = -6b 2. Положим теперь b = 6t 3. Отсюда z = -6t 2,   x = 1 + 6t 3,   y = 1 - 6t 3. Таким образом, получено бесконечное множество решений исходного уравнения, соответствующих целочисленным значениям параметра t

№ 1Решите в целых числах уравнение:а)8х + 14у = 32; б)6х – 15у = 27; в)19х – 5у = 119 № 2.Найдите общий вид целых неотрицательных чисел, дающихпри делении на 7 остаток 3, а при делении на 11 остаток 4. № 3. Разделите 200 на два слагаемых так, чтобы при делении одного на 6, а другого на 11 получились соответственно остатки 5 и 4.

За что ты можешь себя ПОХВАЛИТЬ? Что тебе УДАЛОСЬ на уроке? Над чем еще нужно ПОРАБОТАТЬ? Зачем нам нужен был этот урок?

Урок окончен! Удачи!

ЛитератураПичурин Л.Ф. За страницами учебника алгебры. Книга для учащихся 7-9кл. общелюразоват. учреждений.- М.: Просвещение, 1999.-237 с.Ткачева М.В. Домашняя математика. Книга для учащихся 7 кл. общеобразоват. учреждений. – М. : Просвещение, 1994.- 190с.http://garshin.ru/evolution/mathematics/math-history.html http://www.math.md/school/krujok/diofantr/diofantr.htmlhttp://virlib.eunnet.net/books/numbers/text/5.htmlhttp://maths3.narod.ru/algteo4.html