Презентация на тему: Введение в логику

Введение в логику

Булева алгебра (алгебра логики) изучает свойства функций, у которых и аргументы, и значения принадлежат заданному двухэлементному множеству (например, {0,1}). Дж. Буль (1815 – 1864) – анг. математик отец алгебры логики

Клод Шеннон – отец современных теорий информации и связи В 1938 году защитил докторскую диссертацию, в которой разработал принципы логического устройства компьютера, соединив булеву алгебру с функционированием релейно-контактных и электронно-ламповых схем. Клод Шеннон (1916-2001) – американский математик и инженер

Логическое высказывание - это любое повествовательное пpедлoжение, в oтнoшении кoтopoгo можно oднoзначнo сказать, истинно оно или лoжнo. Примеры:"3 — простое число"- высказывание, так как оно истинное. "Париж — столица Японии" - высказывание, так как оно ложное. Высказываниями не являются, например, предложения "ученик десятого класса" и "информатика — интересный предмет". Первое предложение ничего не утверждает об ученике, а второе использует слишком неопределённое понятие “интересный предмет”. Вопросительные и восклицательные предложения также не являются высказываниями, поскольку говорить об их истинности или ложности не имеет смысла. Предложения типа "в городе A более миллиона жителей", "у него голубые глаза" не являются высказываниями, так как для выяснения их истинности или ложности нужны дополнительные сведения: о каком конкретно городе или человеке идет речь.

Какие из предложений являются высказыванием? Определите их истинность. Какой длины эта лента?Прослушайте сообщение.Число 11 является простым.Делайте утреннюю зарядку!Назовите устройство ввода информации.Кто отсутствует?Все медведи – бурые.

Логические операции

Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение (умозаключение)Логическая переменная – это простое высказывание, содержащее только одну мысль (обозначение А, В, С и т.д.).Значением логического выражения могут быть только ЛОЖЬ (0) или ИСТИНА (1).

Записать в виде логического выражения: «Летом Петя поедет в деревню и, если будет хорошая погода, то он пойдет на рыбалку».Есть два простых высказывания: А – «Число 10 – четное»;В – «Волк травоядное животное».Составьте из них все возможные составные высказывания и определите их истинность.

Задания3. Запишите следующие высказывания в виде логических выражений:А) Число 17 нечетное и двузначное.Б) Неверно, что корова – хищное животное.С) Если компьютер включен, то можно на нем работать.

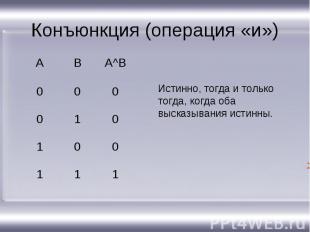
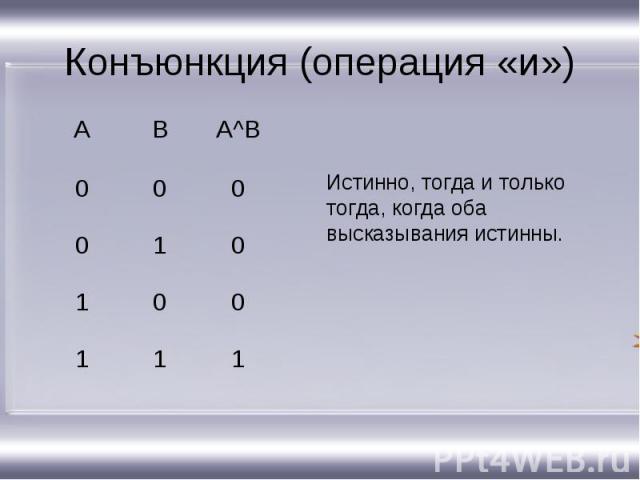
Конъюнкция (операция «и») Истинно, тогда и только тогда, когда оба высказывания истинны.

Дизъюнкция (операция «или») Ложно, тогда и только тогда, когда оба высказывания ложны.

Логическое отрицание (операция «не») Истинно, когда А ложно и ложно, когда А истинно.

Найдите значения логических выражений:F = (0v0)v(1v1)F = (1v1)v(1v0)F = ((1v0)v1)v1)F = (0^1)^1

Задания

Из двух простых высказываний постройте сложное высказывание, используя «и», «или». Запишите логические высказывания с помощью логических операций и определите их истинность:а) На полке стоят учебники. На полке стоят справочники.б) Часть детей – девочки. Остальные – мальчики.

2. Составьте и запишите истинные сложные высказывания из простых с использованием логических операций.а) Любое из чисел X, Y, Z положительно.б) Любое из чисел X, Y, Z отрицательно.в) Хотя бы одно из чисел X, Y, Z не отрицательно.г) Все числа X, Y, Z равны 12.д) Если X делится на 9, то X делится и на 3.е) Если X делится на 2, то оно четное.

3. Даны два простых высказывания A={2*2=4}, B = {2*2=5}.Какие из составных высказываний истинны:A^B; AvB; А; В.4.Найдите значения логических выражений:F =1^(1^1)^1 F = ((1v0)^(1^1))^(0v1)F = ((1^0)v(1^0))v1F = ((1^1)v0)^(0v1)F = ((0^0)v0)^(1v1)