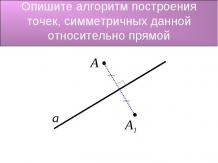
Презентация на тему: «Стереометрия. Аксиомы»

1.Понятия стереометрии 1.Понятия стереометрии 2. Изображение плоскости 3.Аксиомы стереометрии 4.Следствия из аксиом стереометрии

Система аксиом стереометрии состоит из аксиом планиметрии и трех аксиом стереометрии . В аксиомах стереометрии выражены основные свойства неопределяемых понятий: точки, прямой, плоскости и расстояния. Плоскости - это фигуры, на которых выполняется планиметрия и для которых верны аксиомы стереометрии. Пространство - это множество, элементами которого являются точки и в котором выполняется система аксиом стереометрии, описывающая свойства точек, прямых и плоскостей. Стереометрия – раздел геометрии, в котором изучаются свойства фигур в пространстве

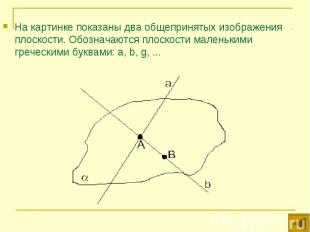
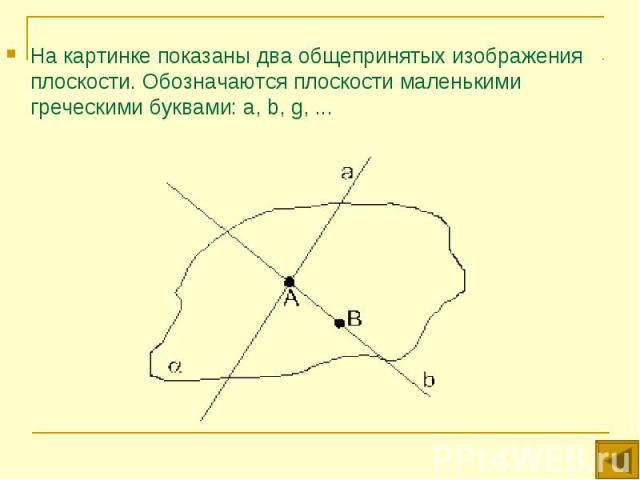
На картинке показаны два общепринятых изображения плоскости. Обозначаются плоскости маленькими греческими буквами: a, b, g, ... На картинке показаны два общепринятых изображения плоскости. Обозначаются плоскости маленькими греческими буквами: a, b, g, ...

Существует хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек. Существует хотя бы одна прямая и хотя бы одна плоскость. Каждая прямая и каждая плоскость есть не совпадающее с пространством непустое множество точек. а

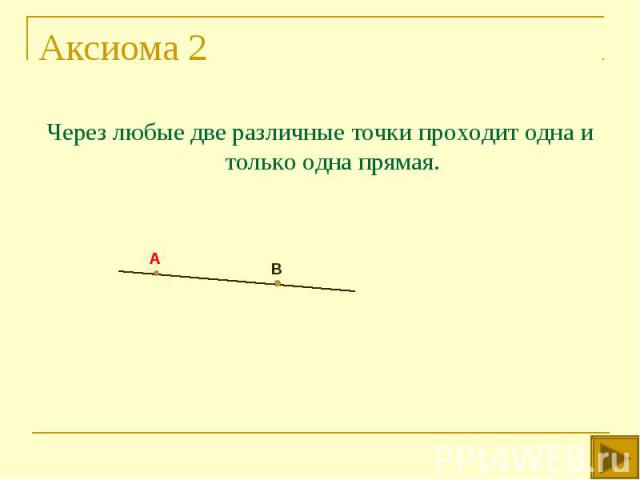
Через любые две различные точки проходит одна и только одна прямая. Через любые две различные точки проходит одна и только одна прямая.

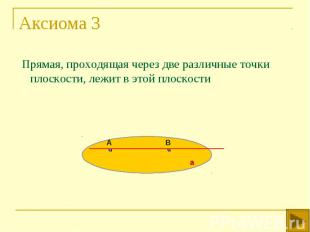
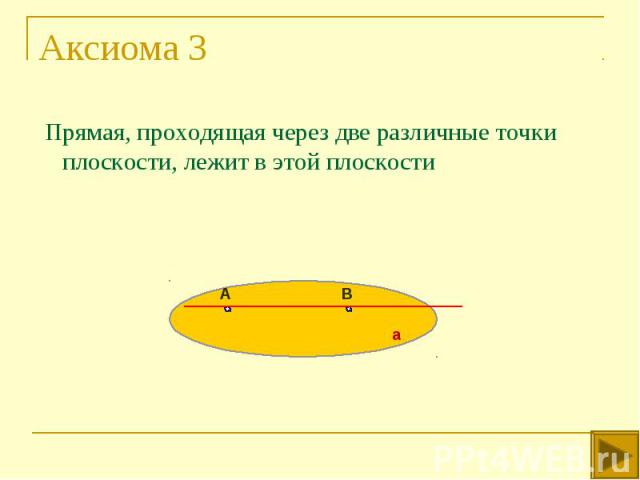
Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости Прямая, проходящая через две различные точки плоскости, лежит в этой плоскости

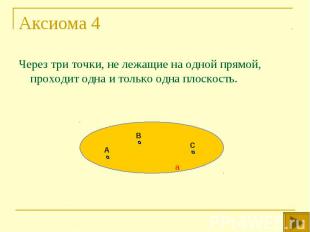
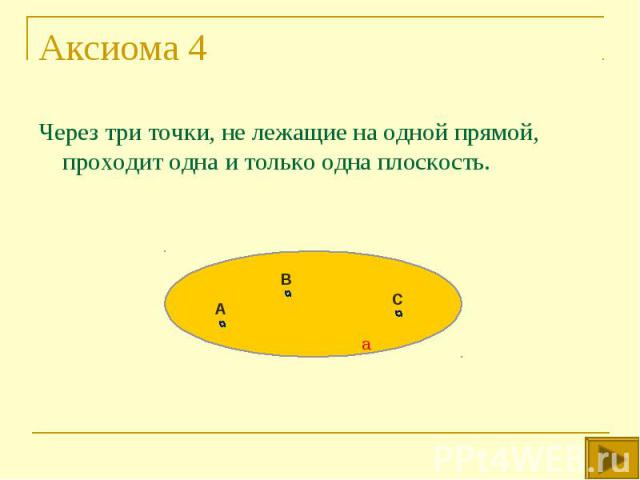
Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость. Через три точки, не лежащие на одной прямой, проходит одна и только одна плоскость.

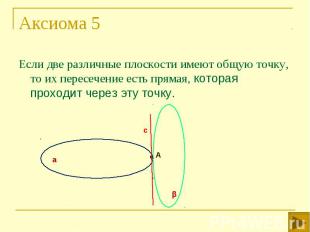
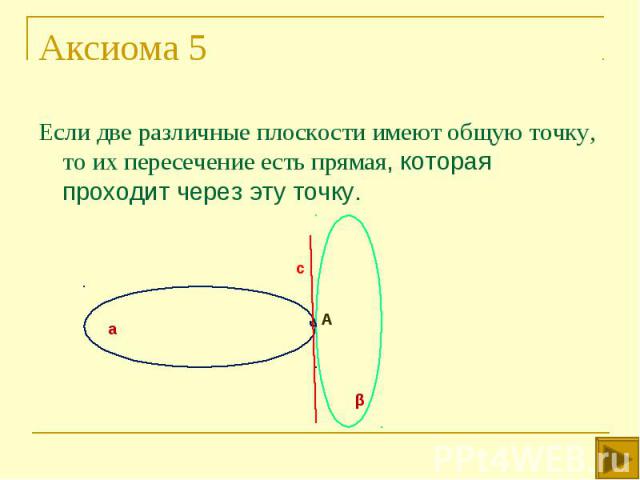
Если две различные плоскости имеют общую точку, то их пересечение есть прямая, которая проходит через эту точку. Если две различные плоскости имеют общую точку, то их пересечение есть прямая, которая проходит через эту точку.

Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние от В до А равно нулю в том и только в том случае, если точки А и В совпадают. Для любых двух точек А и В имеется неотрицательная величина, называемая расстоянием от А до В. Расстояние от В до А равно нулю в том и только в том случае, если точки А и В совпадают.

Расстояние от точки А до точки В равно расстоянию от точки В до точки А: АВ=ВА Расстояние от точки А до точки В равно расстоянию от точки В до точки А: АВ=ВА

Для каждой плоскости выполняются известные из планиметрии аксиомы порядка, подвижности плоскости и параллельных прямых. Для каждой плоскости выполняются известные из планиметрии аксиомы порядка, подвижности плоскости и параллельных прямых.

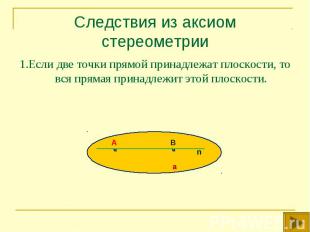
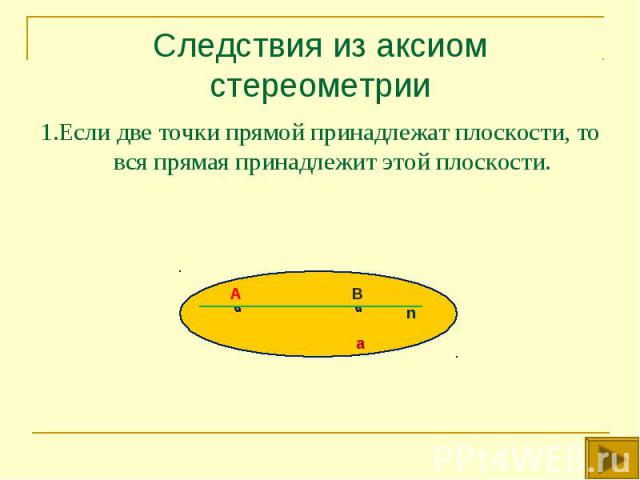
1.Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости. 1.Если две точки прямой принадлежат плоскости, то вся прямая принадлежит этой плоскости.

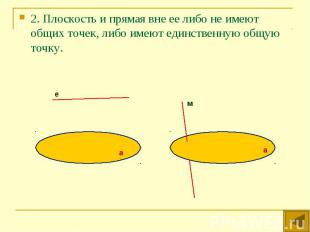
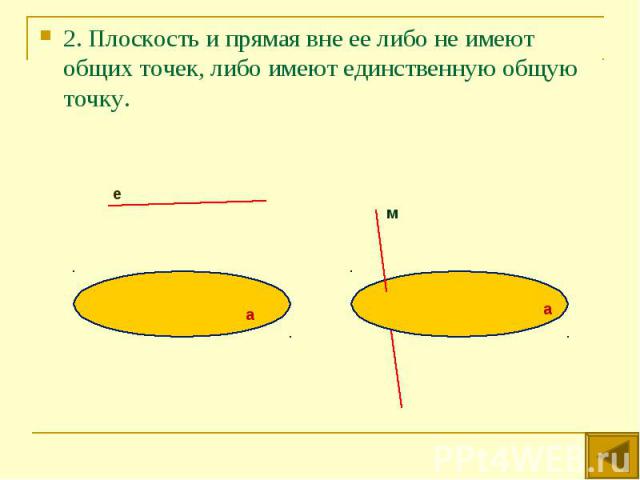
2. Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку. 2. Плоскость и прямая вне ее либо не имеют общих точек, либо имеют единственную общую точку.

г. Белгород, 2010 год г. Белгород, 2010 год Работа Асеевой Валерии Учитель Гринякина Валентина Николаевна Материал взят из учебника геометрии