Презентация на тему: «Такая разная геометрия»

Цели исследования: Изучить исторический материал, связанный с проблемой параллельности прямых. Найти, существует ли доказательство пятого постулата Евклида? Выявить, существуют ли геометрии, отличные от евклидовой?

Геометрия Евклида Первым систематическим изложением геометрии, дошедшим до нашего времени, являются “Начала” – сочинения александрийского математика Евклида.

В “Началах” был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). В “Началах” был развит аксиоматический подход к построению геометрии, который состоит в том, что сначала формулируются основные положения (аксиомы), а затем на их основе посредством рассуждений доказываются другие утверждения (теоремы). Изложение геометрии Евклидом долгое время служило недосягаемым образцом точности, безукоризненности и строгости. Только в начале 20 века математики смогли улучшить логические основания геометрии.

Постулаты Евклида Из каждой точки ко всякой другой точке можно провести прямую; Каждую ограниченную прямую можно продолжить неопределённо; Из любого центра можно описать окружность любого радиуса; Все прямые углы равны; И если прямая, падающая на две прямые, образует внутренние и по одну сторону углы, меньше двух прямых, то продолженные эти прямые неограниченно встретятся с той стороны, где углы меньше двух прямых

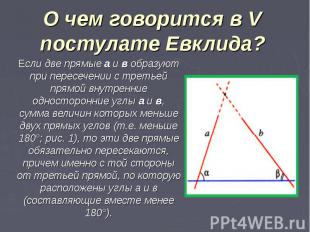
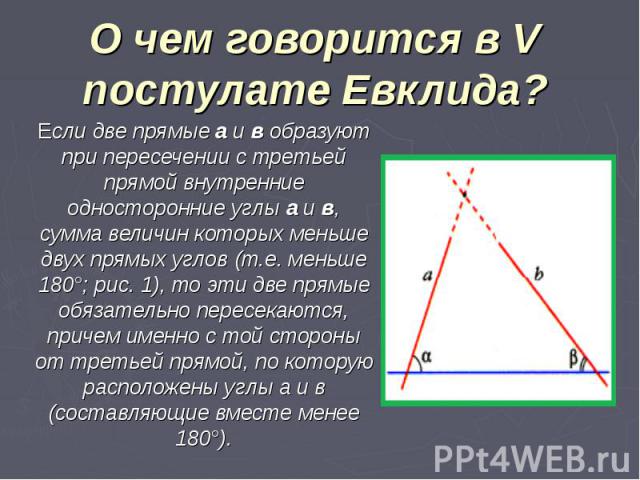
О чем говорится в V постулате Евклида? Если две прямые а и в образуют при пересечении с третьей прямой внутренние односторонние углы a и в, сумма величин которых меньше двух прямых углов (т.е. меньше 180°; рис. 1), то эти две прямые обязательно пересекаются, причем именно с той стороны от третьей прямой, по которую расположены углы а и в (составляющие вместе менее 180°).

Как формулируется равносильная аксиома параллельности? К данной прямой через данную вне ее точку можно провести не более одной параллельной прямой.

Угол в 1 угловую секунду достаточно ощутим (например, при астрономических расчетах). Но проверить, что указанные выше прямые а и в пересекаются на расстоянии 206 км от прямой АВ, совсем не просто. Ведь изготовить плоский лист бумаги и линейку более 200 км не представляется возможным. Использовать оптические приборы? Но тогда надо добавить еще один постулат: свет распространяется по прямой (а это уже не геометрия, а физика). А если сумма углов а и в отличается от 180° еще менее чем на 1 угловую секунду?!

Итак, на базе этих постулатов шло успешное развитие геометрии, но в то время как другие постулаты считались совершенно очевидными, очевидность пятого постулата оспаривалась. Много веков усилия большого числа ученых были направлены на доказательство пятого постулата. Это объяснялось тем, что число аксиом стремились свести к минимуму. Итак, на базе этих постулатов шло успешное развитие геометрии, но в то время как другие постулаты считались совершенно очевидными, очевидность пятого постулата оспаривалась. Много веков усилия большого числа ученых были направлены на доказательство пятого постулата. Это объяснялось тем, что число аксиом стремились свести к минимуму. Ученые думали, что пятый постулат можно доказать как теорему, опираясь на остальные. Многие геометры пытались обойти его, заменяя пятый постулат другим, казавшимся более очевидным. На этом пути было сформулировано много положений, но все они были эквивалентны пятому постулату Евклида.

Например: сумма углов треугольника равна 180°, во всех треугольниках сумма углов одна и та же, через любую точку внутри угла можно провести секущую, пересекающую обе стороны угла, существуют два подобных, но не равных треугольника, теорема Пифагора, для всякого треугольника существует описанная окружность и др.

В конце 18 века у некоторых геометров возникла мысль о невозможности доказать пятый постулат. Допустив, что пятый постулат неверен, математики пытались прийти к логическому противоречию. Они приходили к утверждениям, противоречащим нашей геометрической интуиции, но логического противоречия не получалось. В конце 18 века у некоторых геометров возникла мысль о невозможности доказать пятый постулат. Допустив, что пятый постулат неверен, математики пытались прийти к логическому противоречию. Они приходили к утверждениям, противоречащим нашей геометрической интуиции, но логического противоречия не получалось.

Не может ли быть так, что заменив пятый постулат его отрицанием, мы придём к новой неевклидовой геометрии, которая во многом не согласуется с нашими привычными наглядными представлениями, но, тем не менее не содержит никаких логических противоречий? Не может ли быть так, что заменив пятый постулат его отрицанием, мы придём к новой неевклидовой геометрии, которая во многом не согласуется с нашими привычными наглядными представлениями, но, тем не менее не содержит никаких логических противоречий?

Геометрия Лобачевского Лобачевский построил новую геометрию, откинув постулат Евклида, заменив его другим, прямо противоположным по смыслу: “Через точку А вне прямой а в плоскости, определяемой точкой А и прямой а, проходит по крайней мере две прямые с и в не имеющие общей точки с прямой а”.

И не получил противоречия. И не получил противоречия. Отсюда следует, что таких прямых может быть бесконечное количество. Доказывая много десятков теорем, не обнаруживая логических противоречий, Лобачевскому пришла в голову догадка о непротиворечивости такой геометрии, он назвал её воображаемой. В геометрии Лобачевского сохраняются все теоремы, которые в евклидовой геометрии можно доказать без использования пятого постулата.

Например: вертикальные углы равны; углы при основании равнобедренного треугольника равны; из данной точки можно опустить на данную прямую только один перпендикуляр и др.

Однако, теоремы, где применяется аксиома параллельности прямых, видоизменяются: Теорема о сумме углов треугольника готовит первый “сюрприз”: в геометрии Лобачевского сумма углов любого треугольника меньше 180°. Разность между 180° и суммой углов треугольника положительна и называется дефектом (D) этого треугольника. Формула для площади треугольника S=k*D, то есть площадь связана с его дефектом. Самую большую площадь имеет треугольник с нулевыми углами, а его стороны имеют бесконечную длину

В геометрии Лобачевского: Два неравных равносторонних треугольника имеют неравные углы. В геометрии Лобачевского не существует подобных фигур. Если углы одного треугольника равны соответственно углам другого треугольника, то эти треугольники равны. Геометрическое место точек, находящихся на данном расстоянии от данной прямой и лежащих по одну сторону есть кривая линия, которая называется эквидистантой.

Возможные расположения двух прямых на плоскости Лобачевского: Две несовпадающие прямые либо пересекаются в одной точке, либо параллельны, либо являются расходящимися

Геометрия Римана Через некоторое время идеи Лобачевского были приняты математиками, и следующим этапом развития геометрии стала эллиптическая геометрия Римана. Риман исходил из того, что через точку, не лежащую на данной прямой, вообще нельзя провести прямую, не пересекающую данную.

В геометрии Римана: две прямые всегда пересекаются, параллельных прямых совсем нет; сумма углов прямолинейного треугольника больше 180°; прямая имеет конечную длину, плоскость – конечную площадь и др.

Каково же применение нелинейных геометрий? Геометрии Евклида, Лобачевского и Римана являются в свою очередь частными случаями общей геометрии Римана для многомерных искривлённых пространств.

Современники Лобачевского, потом и Римана отказывались принимать новую геометрию. Но в начале 20 века, как гром среди ясного неба Эйнштейн создаёт теорию относительности, частным случаем которой является теория тяготения Ньютона. Современники Лобачевского, потом и Римана отказывались принимать новую геометрию. Но в начале 20 века, как гром среди ясного неба Эйнштейн создаёт теорию относительности, частным случаем которой является теория тяготения Ньютона. Оказалось, что взаимосвязь пространства и времени, описываемая в теории относительности, имеет непосредственное отношение к геометрии Лобачевского. Например, в расчетах современных синхрофазотронов используются формулы геометрии Лобачевского.

Следствием теории относительности явился в частности тот факт, что наше как мы думали трёхмерное евклидово пространство на самом деле таковым не является. Следствием теории относительности явился в частности тот факт, что наше как мы думали трёхмерное евклидово пространство на самом деле таковым не является. А живём мы в четырёхмерном искривлённом пространстве-времени, которое описывается общей геометрией Римана. Тяготение на самом деле результат искривления пространства вблизи массивных тел. Следствием этого является замедление времени вблизи тяжелых тел, кратчайшее расстояние между точками не прямая, а некоторая кривая и др.

Установлено достоверно замедление времени при скоростях, близких к скорости света. Параметры орбиты Меркурия, самой близкой к Солнцу планеты не укладывались в теорию тяготения Ньютона, а теория относительности смогла это объяснить искривлением пространства вблизи Солнца. Установлено достоверно замедление времени при скоростях, близких к скорости света. Параметры орбиты Меркурия, самой близкой к Солнцу планеты не укладывались в теорию тяготения Ньютона, а теория относительности смогла это объяснить искривлением пространства вблизи Солнца.

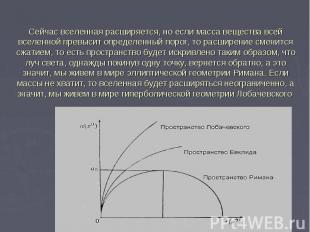
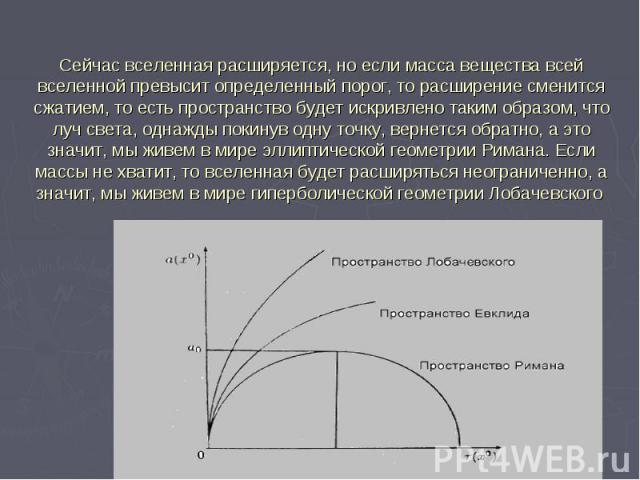
Сейчас вселенная расширяется, но если масса вещества всей вселенной превысит определенный порог, то расширение сменится сжатием, то есть пространство будет искривлено таким образом, что луч света, однажды покинув одну точку, вернется обратно, а это значит, мы живем в мире эллиптической геометрии Римана. Если массы не хватит, то вселенная будет расширяться неограниченно, а значит, мы живем в мире гиперболической геометрии Лобачевского

Исследования Саккери Гипотезу тупого угла, допускающую существование четырехугольника, у которого четвертый угол ф тупой, Саккери отверг при помощи строгого рассуждения. Однако доказать, что и гипотеза острого угла неверна, ни сам Саккери, ни его последователи не смогли. Неприступная "крепость" пятого постулата осталась непокоренной.

Исследования Лежандра Французского математик Адриен Мари Лежандр, в каждом издании книги, посвященной евклидовой геометрии, приводил рассуждение, в котором, по его мнению, доказывался пятый постулат. Но неизменно в следующем издании автор, признавая, что в его рассуждении использовалось некое утверждение (не сформулированное им явно) - "очевидное", но в действительности представлявшее собой новую аксиому, эквивалентную пятому постулату. Ни одна из попыток Лежандра не привела к успеху.

Исследования Гаусса Гаусс обратился к теории параллельных в 1792 г. Сначала он надеялся доказать пятый постулат, но затем пришел к мысли о построении новой геометрии, которую назвал неевклидовой. В 1817 г. в одном из писем признался: "Я прихожу все более к убеждению, что необходимость нашей геометрии не может быть доказана". Но обнародовать эти идеи он не решился из боязни быть непонятым.

Исследования Януша Больяй Творцом новой геометрии стал так же и венгерский математик Янош Больяй (1802 - 1860). В отличие от Гаусса он стремился распространить свои идеи, но большинство математиков тогда еще не были готовы их воспринять. Результаты Яноша Больяя были сжато изложены в 1832 г. в приложении книге его отца, Фаркаша Больяя. Труд Я. Больяя "Приложение, содержащее науку о пространстве, абсолютно истинную, не зависящую от истинности или ложности XI аксиомы Евклида (что a priori никогда решено быть не может)" обычно кратко называют "Аппендикс" (от лат. "приложение").

Исследования Лобачевского Русский математик, профессор Казанского университета Николай Иванович Лобачевский, писал, что задача о параллельных прямых представляет собой "трудность, до сих пор непобедимую, но между тем заключающую в себе истины ощутительные, вне всякого сомнения, и столь важные для целей науки, что никак не могут быть обойдены".