Презентация на тему: Скалярное произведение вектора

Скалярное произведение векторов Скалярным произведением двух ненулевых векторов называется произведение их длин на косинус угла между ними. Если хотя бы один из векторов нулевой, то скалярное произведение таких векторов считается равным нулю. Скалярное произведение векторов и обозначается . По определению, Произведение называется скалярным квадратом и обозначается Из формулы скалярного произведения следует равенство 900igr.net

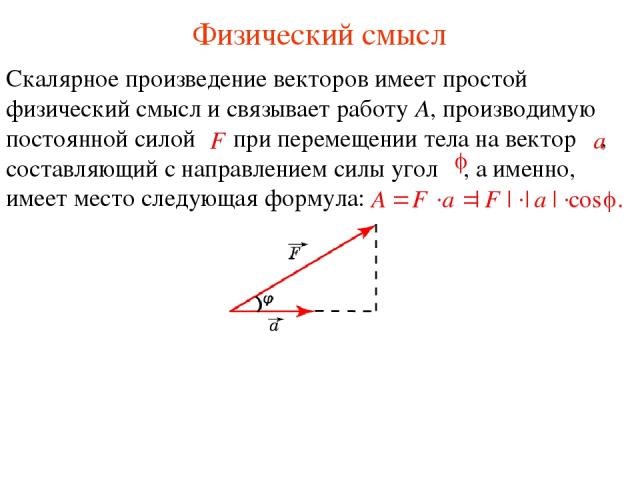
Физический смысл Скалярное произведение векторов имеет простой физический смысл и связывает работу A, производимую постоянной силой при перемещении тела на вектор , составляющий с направлением силы угол , а именно, имеет место следующая формула:

Пример 1 Дан вектор Найдите координаты перпендикулярного к нему вектора.

Пример 2 Найдите угол A треугольника с вершинами

Упражнение 1 Вычислите скалярное произведение двух векторов и , если = 2, = 3, а угол между ними равен: а) 45°; б) 90°; в) 135°. б) 0;

Упражнение 2 В равностороннем треугольнике АВС со стороной 1 проведена высота BD. Вычислите скалярное произведение векторов: а) и б) и в) и . б) 0; в) 1.

Упражнение 3 Ответ: –4. Найдите скалярное произведение векторов (-1, 2) и (2,-1).

Упражнение 4 Охарактеризуйте угол между векторами и , если: а) б) в) г) Ответ: а) 0о< < 90о; б) 90о< < 180о ; в) = 90о; г) = 180о.

Упражнение 5 Ответ: а) = 0о; Длины векторов и равны 1. При каком угле между ними скалярное произведение будет: а) наибольшим; б) наименьшим? б) = 180о.

Упражнение 6 Найдите угол между векторами (1, 2) и (1, 0).

Упражнение 7 Ответ: 60о. Какой угол образуют единичные векторы и , если известно, что и взаимно перпендикулярны.

Упражнение 8 Ответ: t = 0. При каком значении t вектор перпендикулярен вектору , если (2, -1), (4, 3).

Упражнение 9 Ответ: а) 36; Для прямоугольника ABCD со сторонами AB = 6 см, AD = 8 см найдите скалярное произведение: а) б) в) г) где E и F – середины сторон AD и CD соответственно. б) 68; в) 82; г) 50.

Упражнение 10 Ответ: A = 17. Вычислите, какую работу A производит сила (-3, 4), когда ее точка приложения, двигаясь прямолинейно, перемещается из положения B(5, -1) в положение C(2, 1).