Презентация на тему: Симметрия правильных многогранников

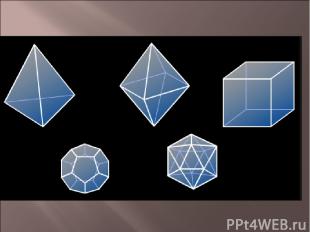
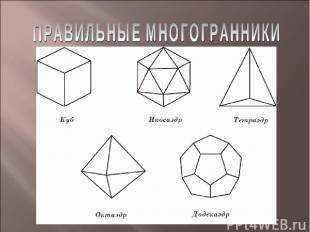
Одно из древнейших упоминаний о правильных многогранниках находится в трактате Платона (427-347 до н. э.) "Тимаус". Поэтому правильные многогранники также называются платоновыми телами. Каждый из правильных многогранников, а всего их пять, Платон ассоциировал с четырьмя "земными" элементами: земля (куб), вода (икосаэдр), огонь (тетраэдр), воздух (октаэдр), а также с "неземным" элементом - небом (додекаэдр).

Знаменитый математик и астроном Кеплер построил модель Солнечной системы как ряд последовательно вписанных и описанных правильных многогранников и сфер.

Одно из них звучит так: многогранник называется правильным, если существуют три концентрические сферы, одна из которых касается всех граней многогранника, другая касается всех его ребер и третья содержит все его вершины. Это определение напоминает одно из возможных определений правильного многоугольника: многоугольник называется правильным, если он вписан в некоторую окружность и описан около другой окружности, причем эти окружности концентричны.

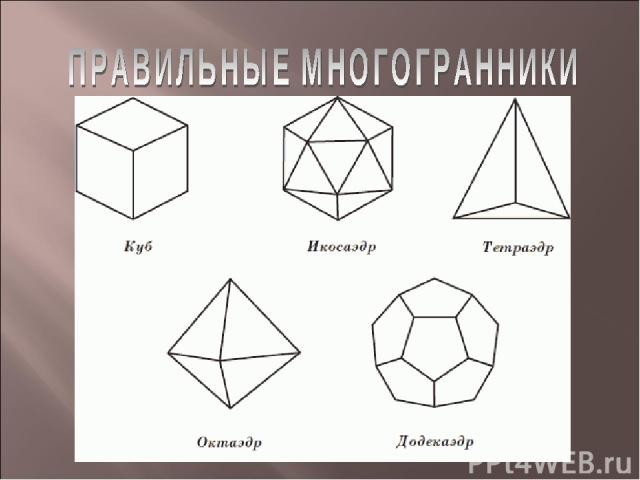
правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны.

он выпуклый все его грани являются равными правильными многоугольниками в каждой его вершине сходится одинаковое число граней все его двугранные углы равны

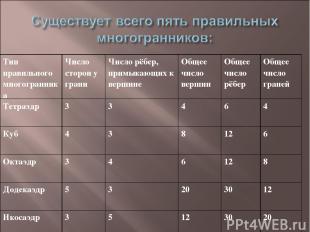
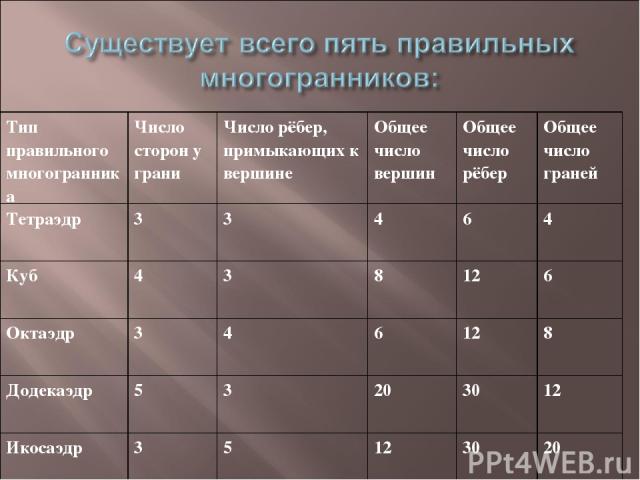
Тип правильного многогранника Число сторон у грани Число рёбер, примыкающих к вершине Общее число вершин Общее число рёбер Общее число граней Тетраэдр 3 3 4 6 4 Куб 4 3 8 12 6 Октаэдр 3 4 6 12 8 Додекаэдр 5 3 20 30 12 Икосаэдр 3 5 12 30 20

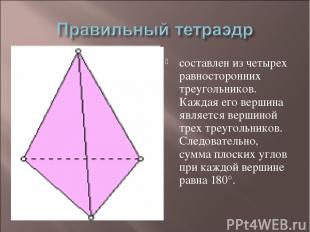
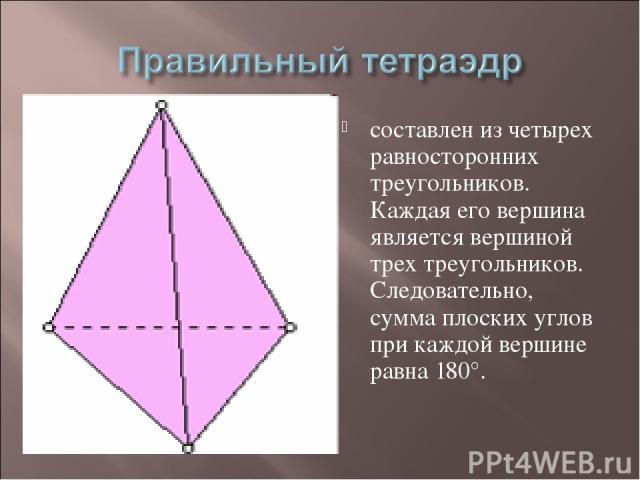
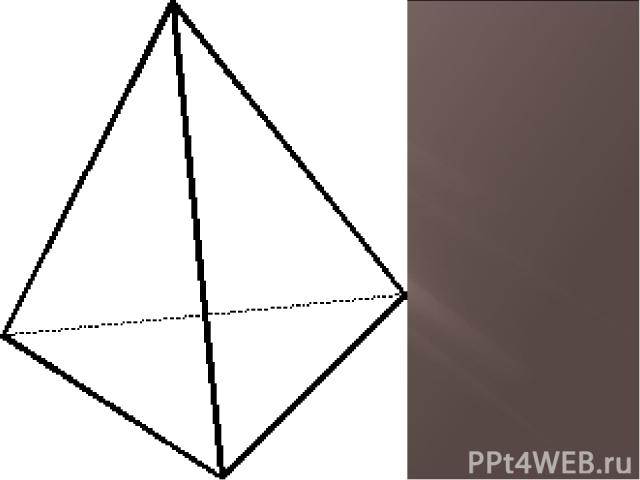
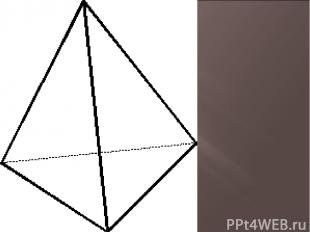
составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.

Тетраэдр не имеет центра симметрии, но имеет 3 оси симметрии и 6 плоскостей симметрии.

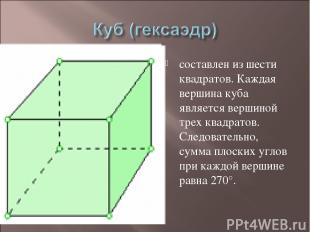
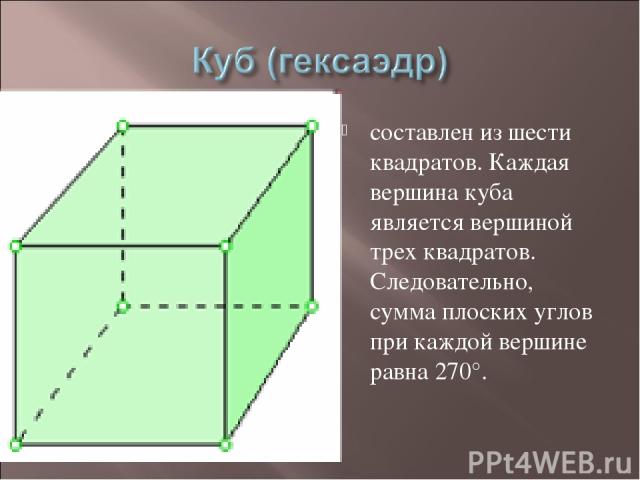
составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270°.

Куб имеет центр симметрии - центр куба, 9 (? – уточните!) осей симметрии и 9 плоскостей симметрии.

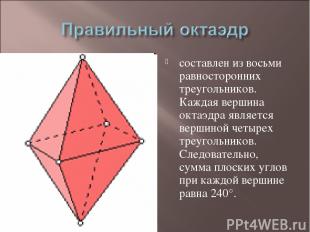
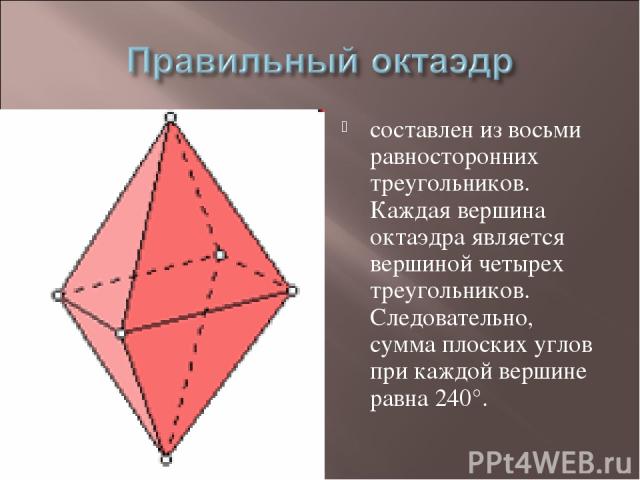
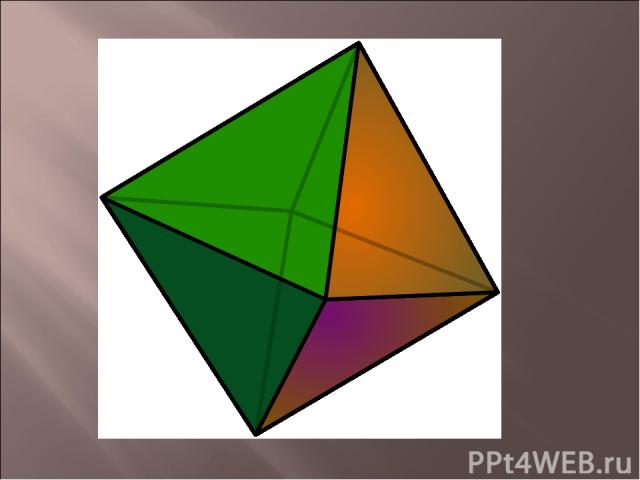
составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240°.

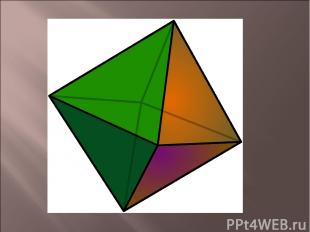
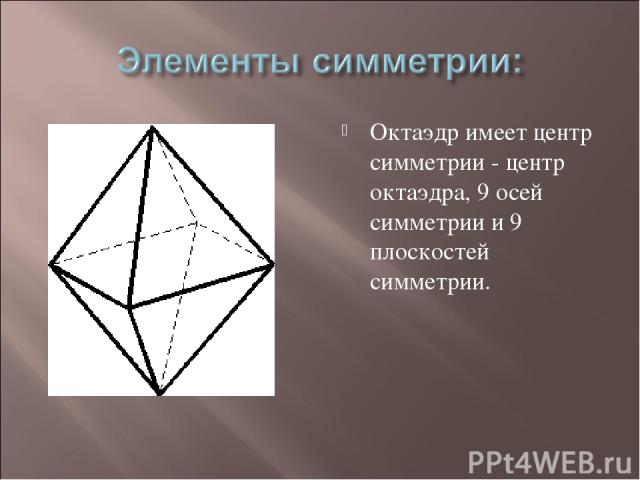
Октаэдр имеет центр симметрии - центр октаэдра, 9 осей симметрии и 9 плоскостей симметрии.

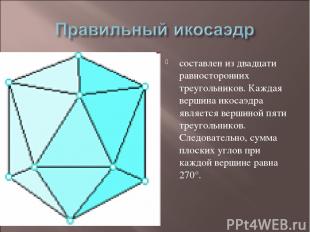
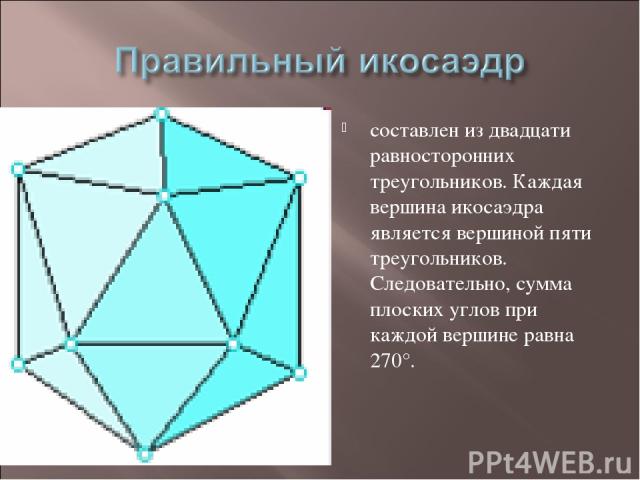
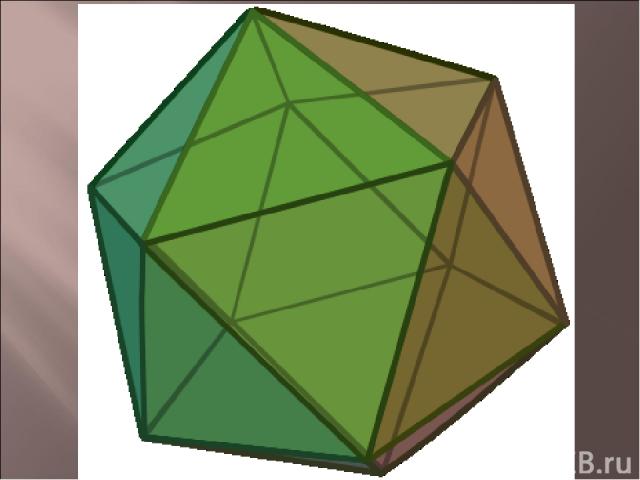
составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 270°.

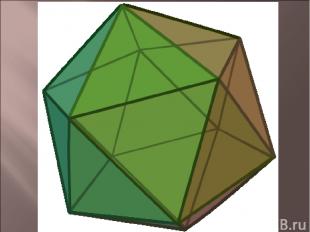
Икосаэдр имеет центр симметрии - центр икосаэдра, 15 осей симметрии и 15 плоскостей симметрии.

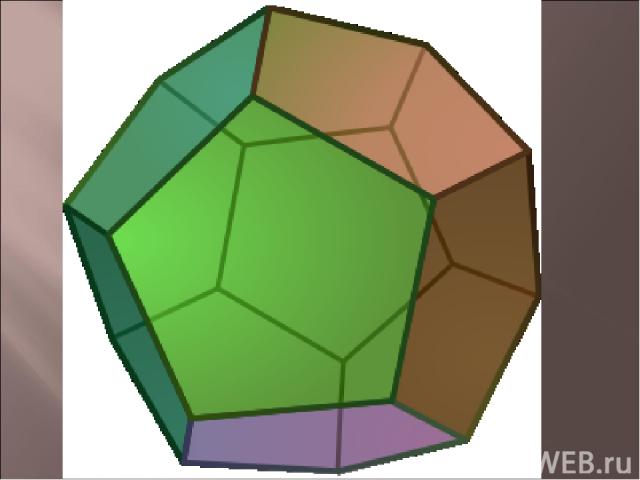
составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.

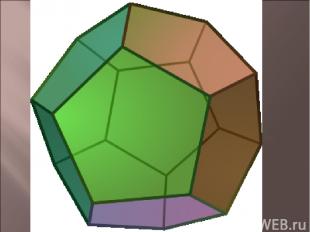
Додекаэдр имеет центр симметрии - центр додекаэдра, 15 осей симметрии и 15 плоскостей симметрии.

«Симметрия … есть идея, с помощью которой человек веками пытался объяснить и создать порядок, красоту и совершенство». Герман Вейль А А1 Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.

Точки А и А1 называются симметричными относительно прямой (ось симметрии), если прямая проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка прямой а считается симметричной самой себе. Лист, снежинка, бабочка – примеры осевой симметрии. А1

«Что может быть более похоже на мою руку или мое ухо, чем их собственное отражение в зеркале? И все же руку, которую я вижу в зеркале, нельзя поставить на место постоянной руки…» Иммануил Кант Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.

Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии фигуры, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией.

«Раз, стоя перед черной доской и рисуя на ней мелом разные фигуры, я вдруг был поражен мыслью: почему симметрия приятна для глаз? Что такое симметрия? Это врожденное чувство, отвечал я сам себе. На чем же оно основано? Разве во всем в жизни есть симметрия?» Л. Толстой «Отрочество» Кристалл аметиста Кристаллы льда

Церковь Покрова Богородицы на Нерли

Кижи. Слева церковь Преображения. 1714 г.

Здание МГУ

Микеланджело. Гробница Джулиано Медичи

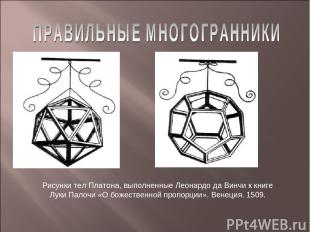
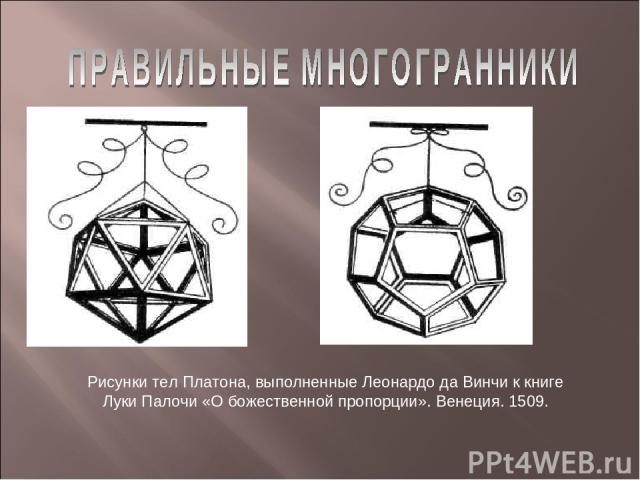
Рисунки тел Платона, выполненные Леонардо да Винчи к книге Луки Палочи «О божественной пропорции». Венеция. 1509.

С. Дали. Тайная вечеря