Презентация на тему: Скалярное произведение в координатах

Скалярное произведение в координатах и его свойства. 5klass.net

1. Сформулируйте теорему синусов. 2. Сформулируйте теорему косинусов. 3. Что значит «решить треугольник»? 4. Какое наименьшее число элементов надо знать, что бы «решить треугольник»? 5. Сформулируйте определение скалярного произведения векторов. Проверка домашнего задания, математическая разминка.

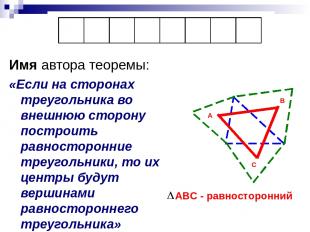
Имя автора теоремы: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника» А В С АВС - равносторонний

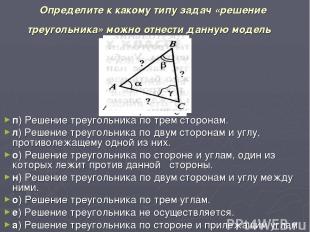
п) Решение треугольника по трем сторонам. л) Решение треугольника по двум сторонам и углу, противолежащему одной из них. о) Решение треугольника по стороне и углам, один из которых лежит против данной стороны. н) Решение треугольника по двум сторонам и углу между ними. о) Решение треугольника по трем углам. е) Решение треугольника не осуществляется. а) Решение треугольника по стороне и прилежащим углам. Определите к какому типу задач «решение треугольника» можно отнести данную модель

7) Результатом скалярного произведения векторов является … а) вектор. о) число. л) градус. 8) Скалярный квадрат координатного вектора равен: т) -1. р) 0. н) 1.

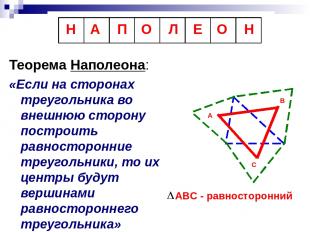
Теорема Наполеона: «Если на сторонах треугольника во внешнюю сторону построить равносторонние треугольники, то их центры будут вершинами равностороннего треугольника» А В С АВС - равносторонний Н А П О Л Е О Н

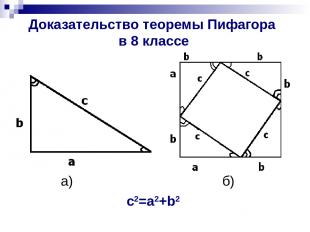
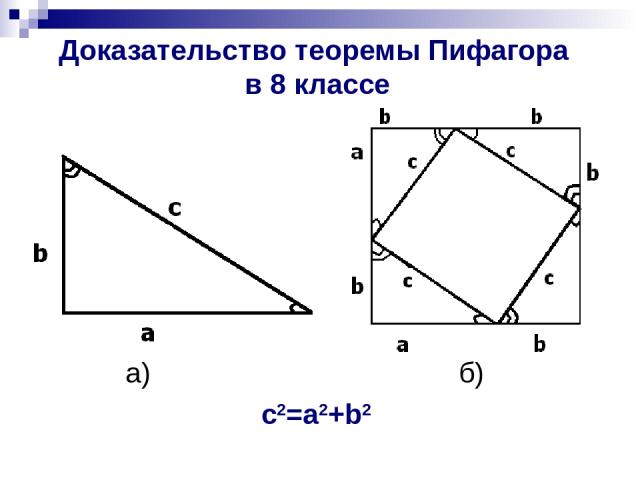
Доказательство теоремы Пифагора в 8 классе а) б) c2=a2+b2

Математический тест Запишите в карточке для ответов свой вариант и Ф.И.

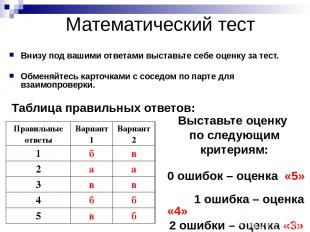
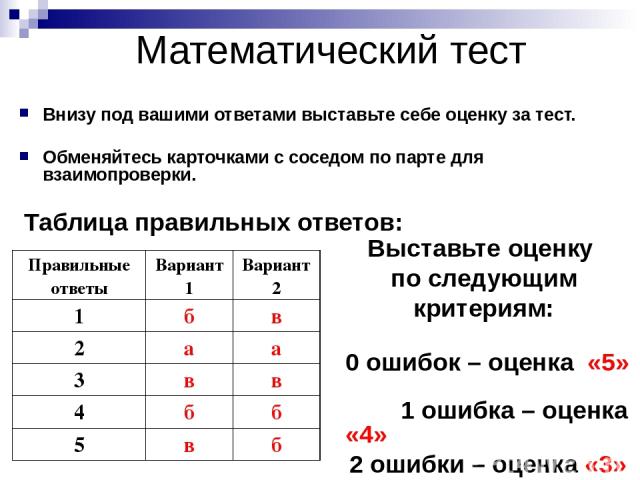
Математический тест Внизу под вашими ответами выставьте себе оценку за тест. Обменяйтесь карточками с соседом по парте для взаимопроверки. Таблица правильных ответов: Выставьте оценку по следующим критериям: 0 ошибок – оценка «5» 1 ошибка – оценка «4» 2 ошибки – оценка «3» 3-5 ошибок – оценка «2». Правильные ответы Вариант1 Вариант 2 1 б в 2 а а 3 в в 4 б б 5 в б

Новый материал Теорема Скалярное произведение векторов и выражается формулой:

Следствие 1. Следствие 2.

Свойства скалярного произведение векторов Действия над векторами (свойства) Закон Действия над числами (свойства) a , b и с –любые числа - любые вектора k – любое число 1 переместительный 2 распределительный 3 сочетательный 4

Решим задание В классе: №1044 (а) 1047 (а) Самостоятельно: №1044 (в) 1047 (в) 1045

Домашнее задание: П. 103,104 № 1044(б), 1047(б).

«Геометрия является самым могущественным средством для развития наших умственных способностей и дает нам возможность правильно мыслить и рассуждать» Галилео Галилей