Презентация на тему: Правильный многогранник

ПРАВИЛЬНЫЕ МНОГОГРАННИКИ 900igr.net

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук». Льюис Кэролл

ПРАВИЛЬНЫЙ МНОГОГРАННИК- выпуклый многогранник, все грани которого – равные правильные многоугольники и в каждой вершине которого сходится одно и то же число ребер.

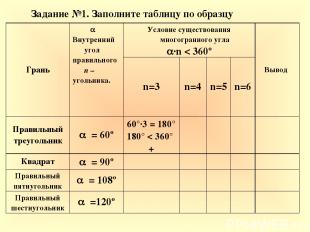
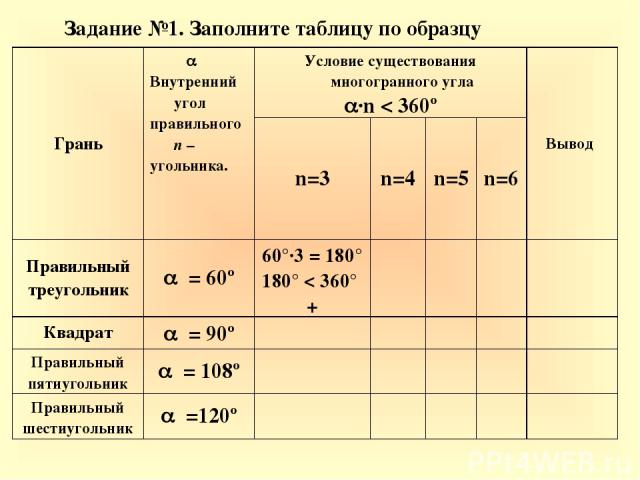
Задание №1. Заполните таблицу по образцу Грань Внутренний угол правильного n – угольника. Условие существования многогранного угла ·n < 360º Вывод n=3 n=4 n=5 n=6 Правильный треугольник = 60º 60°·3 = 180° 180° < 360° + Квадрат = 90º Правильный пятиугольник = 108º Правильный шестиугольник =120º

Существует 3 вида правильных многогранников, гранями которых являются правильные треугольники. Тетраэдр Октаэдр Икосаэдр

Существует 1 вид правильного многогранника, гранями которого являются квадраты. Существует 1 вид Правильного многогранника, гранями которого являются правильные пятиугольники. Гексаэдр (куб) Додекаэдр

«эдра» - грань «тетра» - 4 «гекса» - 6 «окта» - 8 «икоса» - 20 «додека» - 12 Почему правильные многогранники получили такие имена? Это связано с числом их граней. В переводе с греческого языка:

Гексаэдр Тетраэдр Октаэдр Икосаэдр Додекаэдр Платоновы тела

Правильные многогранники иногда называют платоновыми телами, поскольку они занимают видное место в философской картине мира, разработанной великим мыслителем Древней Греции Платоном Платон (ок. 428 – ок. 348 до н.э.)

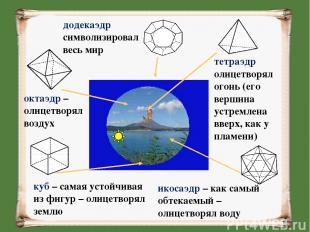
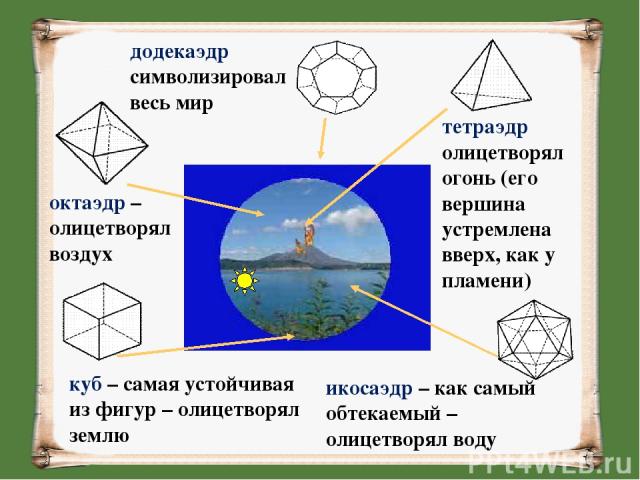
тетраэдр олицетворял огонь (его вершина устремлена вверх, как у пламени) октаэдр – олицетворял воздух куб – самая устойчивая из фигур – олицетворял землю икосаэдр – как самый обтекаемый – олицетворял воду додекаэдр символизировал весь мир

Правильные многогранники в живой и неживой природе

Правильные многогранники в живой природе Скелет одноклеточного организма феодарии по форме напоминает икосаэдр.

Головка вируса-бактериофага имеет форму икосаэдра Вирус полиомиелита имеет форму додекаэдра. Он может жить и размножаться только в клетках человека и приматов.

  Кристаллическая решётка метана имеет форму тетраэдра. Метан  горит бесцветным пламенем. С воздухом образует взрывоопасные смеси. Используется как топливо. Метан

Поваренная соль   Все кристаллы поваренной соли имеют одинаковую кубическую форму. Маленькие шарики – ионы натрия, большие – ионы хлора.

Часто представлен кристаллами в виде кубов, на гранях которых почти всегда наблюдается характерная штриховка. Окрас – желтый с разными оттенками. Окраска и определила название – «пирос» (по-гречески значит «огонь»). Сырье для получения серной кислоты; руда золота, меди, кобальта. Пирит

Магнетит Обычно встречается в виде мелких зерен, но может образовывать кристаллы в форме октаэдра. Встречается в кварцитах и кристаллических сланцах.

Кристаллы алмаза представляют собой гигантские полимерные молекулы и обычно имеют форму октаэдров, реже — кубов или тетраэдров. Алмаз

Алмаз «Кохинор»

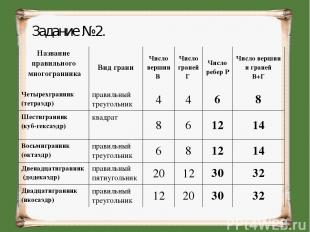
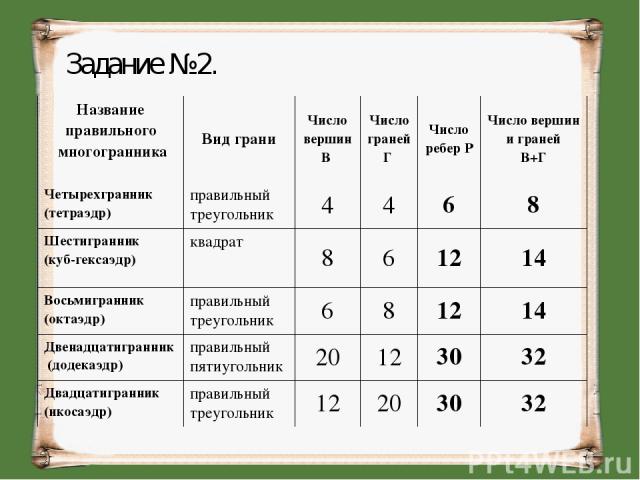
Задание №2. Название правильного многогранника Вид грани Число вершин В Число граней Г Число ребер Р Число вершин и граней В+Г Четырехгранник (тетраэдр) правильный треугольник 4 4 6 8 Шестигранник (куб-гексаэдр) квадрат 8 6 12 14 Восьмигранник (октаэдр) правильный треугольник 6 8 12 14 Двенадцатигранник (додекаэдр) правильный пятиугольник 20 12 30 32 Двадцатигранник (икосаэдр) правильный треугольник 12 20 30 32

Леонард Эйлер (1707 – 1783 гг.) Формула Эйлера Г + В – Р = 2 Теорема Декарта-Эйлера В любом выпуклом многограннике сумма числа граней и числа вершин больше числа ребер на 2