Презентация на тему: Построение сечений многогранников

900igr.net

Цели урока Ввести понятие секущей плоскости. Повторить аксиомы стереометрии. Повторить свойства прямых и плоскостей. Показать на примерах способы построения сечений многогранников. Выработать алгоритм построения сечений тетраэдра и параллелепипеда. Проверить усвоение материала с помощью теста.

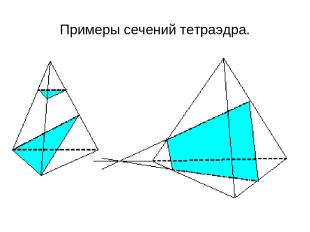
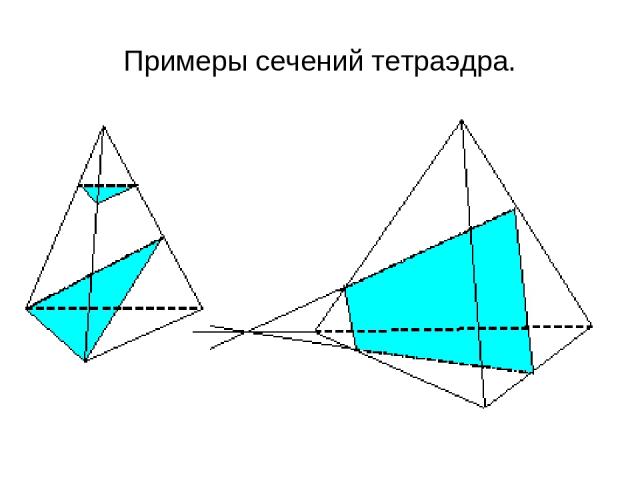
Примеры сечений тетраэдра.

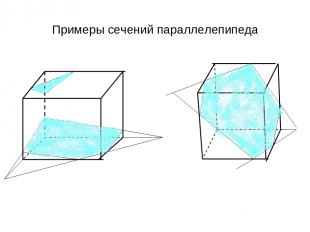
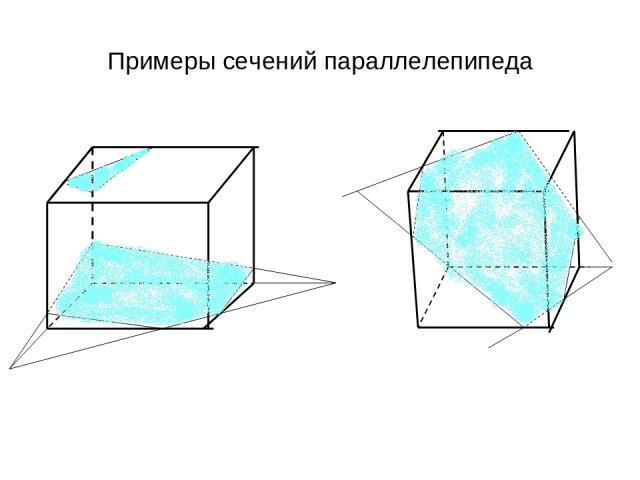
Примеры сечений параллелепипеда

Методы построения сечений Метод следа. В общем случае плоскость сечения имеет общую прямую с плоскостью каждой грани многогранника. Прямую, по которой секущая плоскость пересекает какую-либо грань называют следом секущей плоскости. Метод внутреннего проектирования. Этот метод удобен при построении сечений в тех случаях, когда почему-либо неудобно находить след секущей плоскости, например, след получается очень далеко от заданной фигуры. Используется метод параллельного проецирования. Комбинированный метод. При построении этим методом на каких-то этапах применяются приемы, изложенные в методе следов или методе внутреннего проектирования, а на других этапах применяются теоремы, изученные в разделе «Параллельность прямых и плоскостей».

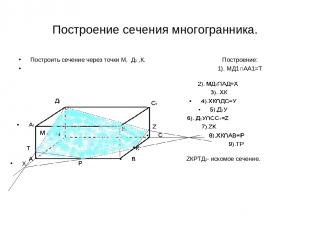
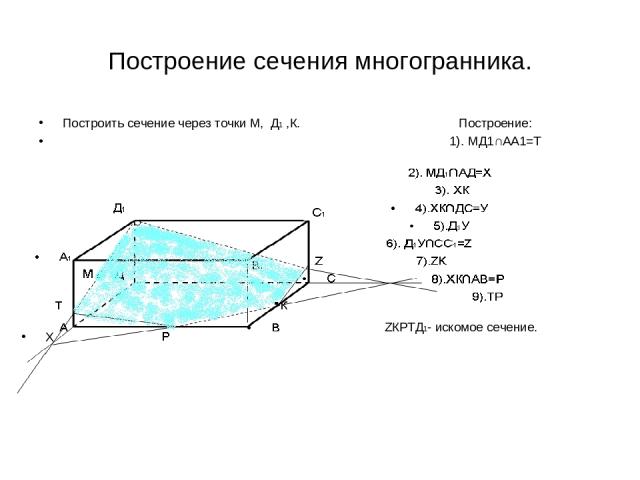
Построение сечения многогранника. Построить сечение через точки М, Д1 ,К. Построение: 1). МД1∩АА1=Т Д1ТРКZ-искомое сечение ZКРТД1- искомое сечение. Х

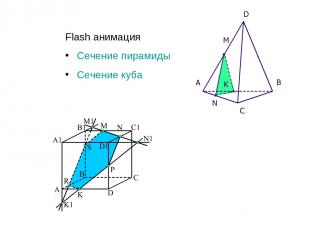
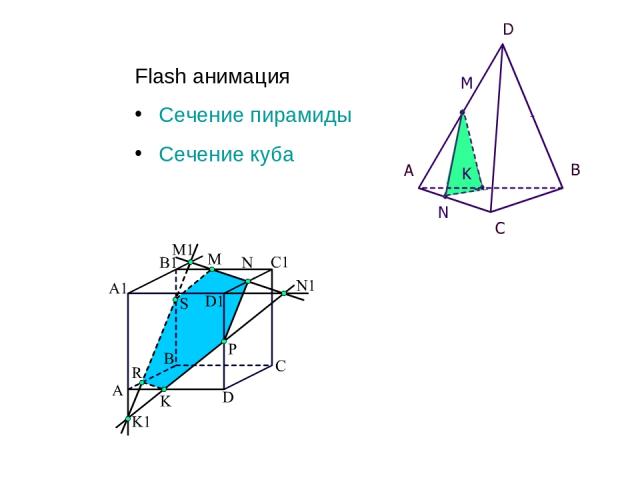
Flash анимация Сечение пирамиды Сечение куба