Презентация на тему: Построение правильных многоугольников

Правильные многоугольники 9кл. Геометрия 900igr.net

Работу выполнила учитель математики МОУ «Гимназия №11» Лисицына Е.Ф.

Выпуклый многоугольник называется правильным, если у него все углы равны и все стороны равны

Известно, что сумма всех внутренних углов выпуклого n-угольника равна (n-2)·180º α=60º α=90º α= n - 2 n ·180º α=108º α=120º 180º 360º 540º 720º

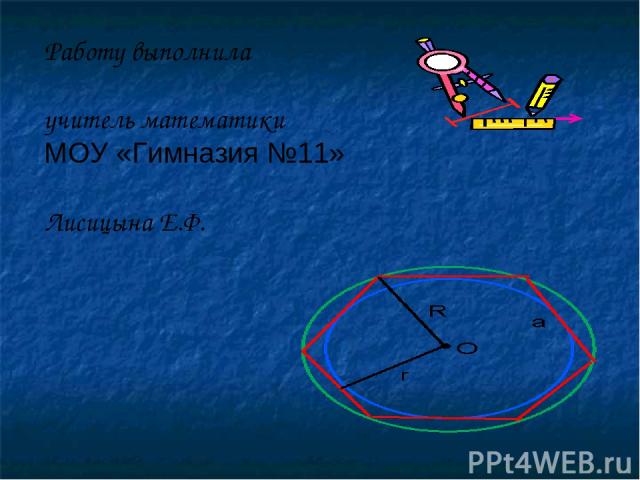
Правильный многоугольник является вписанным в окружность и описанным около окружности, причем центры этих окружностей совпадают.

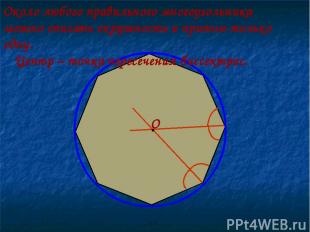
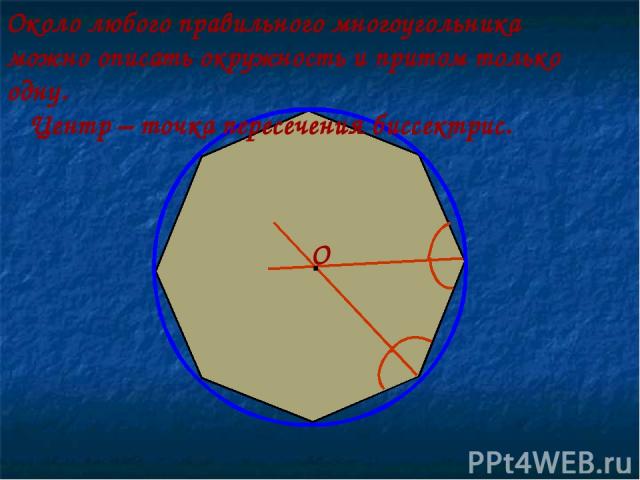
Около любого правильного многоугольника можно описать окружность и притом только одну. Центр – точка пересечения биссектрис. · О

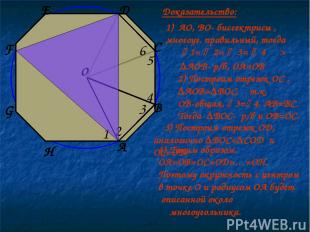
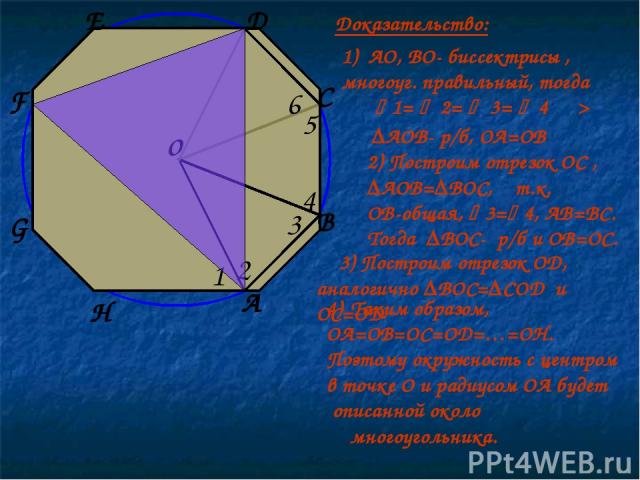
o 1 2 3 4 5 6 1) АО, ВО- биссектрисы , многоуг. правильный, тогда 1= 2= 3= 4 ═> ∆АОВ- р/б, ОА=ОВ 2) Построим отрезок ОС , ∆АОВ=∆ВОС, т.к. ОВ-общая, 3= 4, АВ=ВС. Тогда ∆ВОС- р/б и ОВ=ОС. А В С D 3) Построим отрезок ОD, аналогично ∆ВОС=∆СОD и ОС=ОD E F G H Таким образом, OA=OB=OC=OD=…=OH. Поэтому окружность с центром в точке О и радиусом ОА будет описанной около многоугольника. Доказательство:

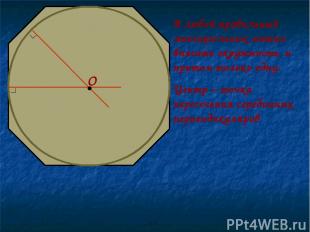
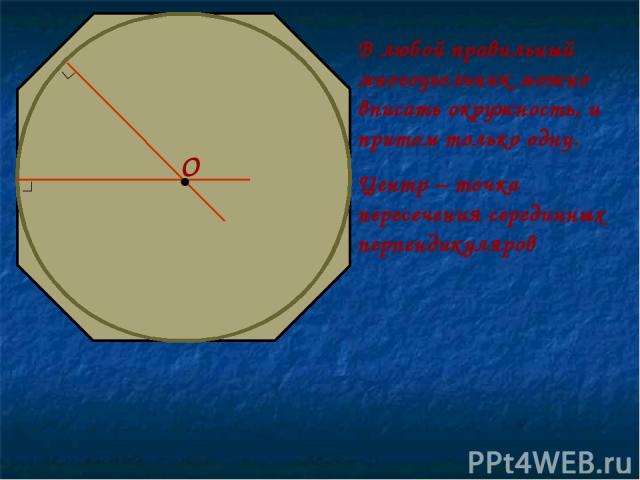
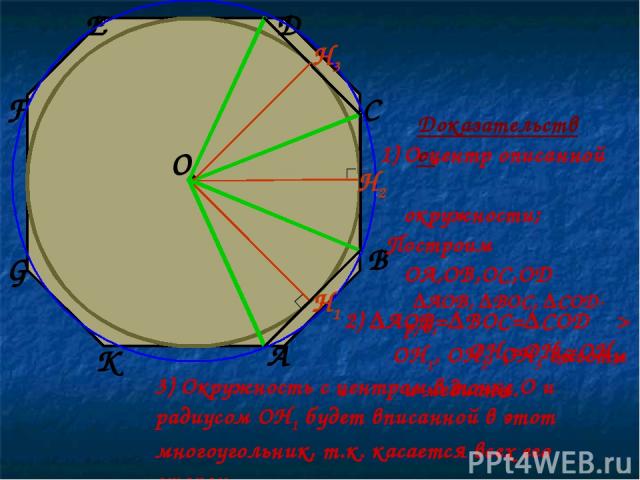
В любой правильный многоугольник можно вписать окружность, и притом только одну. Центр – точка пересечения серединных перпендикуляров • О ∟ ∟

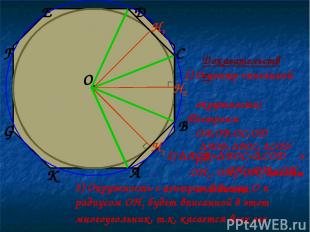
• ∟ ∟ Доказательство: A B C D E F G K ∟ О-центр описанной окружности; Построим ОА,ОВ,ОС,OD ∆AOB, ∆BOC, ∆COD-р/б, OH1, OH2, OH3-высоты и медианы. 2) ∆AOB=∆BOC=∆COD ═> OH1=OH2=OH3. 3) Окружность с центром в точке О и радиусом OH1 будет вписанной в этот многоугольник, т.к. касается всех его сторон. H1 H2 H3 O

Простейшее построение правильного четырехугольника Построение правильного восьмиуголь- ника

Построение правильных многоугольников, то есть деление окружности на равные части, позволяло решать практические задачи: 1)Создание колеса со спицами; 2)Деление циферблата часов; 3)Строительство античных театров; 4)Создание астрономических сооружений

Именно в школе ПИФАГОРА зародилось учение о правильных многоугольниках; кроме того, пифагорейцы рассмотрели вопрос покрытия плоскости правильными многоугольниками.

По некоторым источникам, он являлся автором сочинения о правильных многоугольниках, часто присоединяемого к "Началам" в качестве XV книги. Исидор из Милета (532-537 гг.) - византийский архитектор и геометр, построивший вместе с Анфи - мием собор Святой Софии в Константинополе.

Описал построение правильных 3 , 4 , 5 , 6- угольников, построил правильный 15-угольник

Развитие готического стиля и широкое применение витражей в строительстве соборов также заставило вернуться к задачам построения правильных многоугольников.

Именно Альбрехт Дюрер осуществил новое построение правильного пятиугольника, передав потомкам средневековый способ построения постоянным раствором циркуля.

Дюрер занимался фортификацией, разрабатывая системы оборонительных сооружений; Решил задачу построения правильного восьмиугольника; Разработал принципы черчения художественно исполненных букв.

Для своего друга Луки Пачоли Леонардо, глубоко интересующийся пропорциями, создал иллюстрации многогранников, гранями которых являются правильные многоугольники.

математик Иоганн Кеплер создал трактат «Новогодний подарок или о шестиугольных снежинках», опубликованный в 1611 году. В нем он практически привел первый пример разбиения плоскости на правильные шестиугольники.

Доказал возможность построения правильного 17-угольника. После этого 19-летний юноша решил заняться математикой, а не филологией.

ЗАКЛЮЧЕНИЕ ПРАВИЛЬНЫЕ МНОГОУГОЛЬНИКИ ДОСТОЙНЫ И ВАШЕГО ПРИСТАЛЬНОГО ВНИМАНИЯ. ВОЗМОЖНО,ИМЕННО ВЫ СОВЕРШИТЕ НОВЫЕ ОТКРЫТИЯ. ЖЕЛАЮ УСПЕХА!