Презентация на тему: Виды правильных многогранников

Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Многогранник – это геометрическое тело, ограниченное со всех сторон плоскими многоугольниками, называемыми гранями. Стороны граней – рёбра многогранника, а концы рёбер – вершины многогранника. Многогранник называется выпуклым, если он весь расположен по одну сторону от плоскости, каждой из его граней. Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники, в каждой вершине сходится одно и то же число рёбер, а соседние грани образуют равные углы. Надо отметить, что Платоновых тел ровно пять – ни больше, ни меньше. О них и их свойствах пойдет речь ниже…

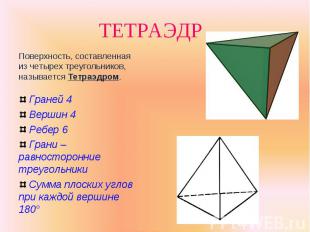
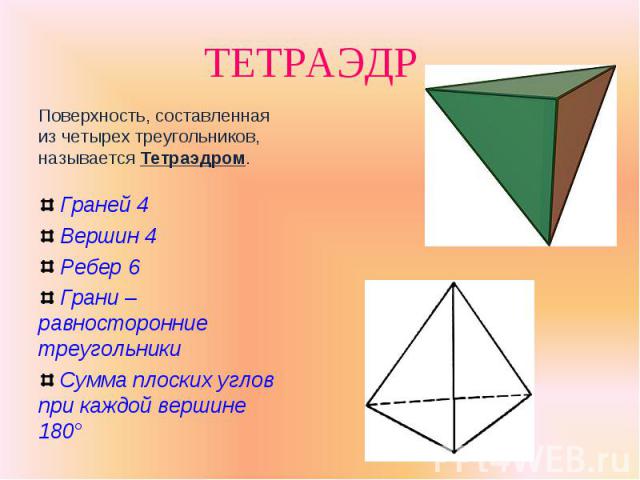
Поверхность, составленная из четырех треугольников, называется Тетраэдром. Поверхность, составленная из четырех треугольников, называется Тетраэдром. Граней 4 Вершин 4 Ребер 6 Грани – равносторонние треугольники Сумма плоских углов при каждой вершине 180°

Поверхность, составленная из 6 квадратов, называется Гексаэдром. Поверхность, составленная из 6 квадратов, называется Гексаэдром. Граней 6 Вершин 8 Ребер 12 Грани – квадраты Сумма плоских углов при каждой вершине 180°

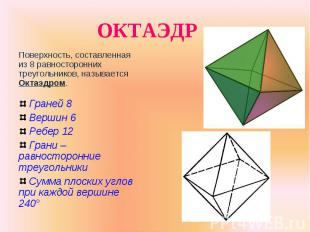
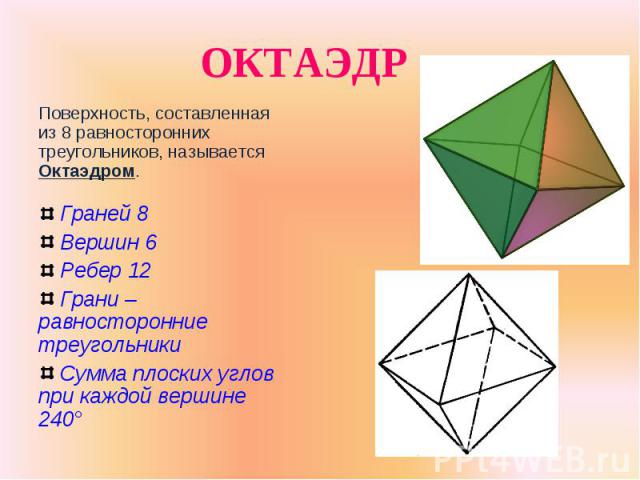
Поверхность, составленная из 8 равносторонних треугольников, называется Октаэдром. Поверхность, составленная из 8 равносторонних треугольников, называется Октаэдром. Граней 8 Вершин 6 Ребер 12 Грани – равносторонние треугольники Сумма плоских углов при каждой вершине 240°

Площадь октаэдра: Площадь октаэдра:

Поверхность, составленная из 12 правильных пятиугольников, называется Додекаэдром. Поверхность, составленная из 12 правильных пятиугольников, называется Додекаэдром. Граней 12 Вершин 20 Ребер 30 Грани – правильные пятиугольники Сумма плоских углов при каждой вершине 324°

Поверхность, составленная из 20 равносторонних треугольников, называется Икосаэдром. Поверхность, составленная из 20 равносторонних треугольников, называется Икосаэдром. Граней 20 Вершин 12 Ребер 30 Грани – равносторонние треугольники Сумма плоских углов при каждой вершине 300°

Икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба Икосаэдр можно вписать в куб, при этом шесть взаимно перпендикулярных рёбер икосаэдра будут расположены соответственно на шести гранях куба, остальные 24 ребра внутри куба, все двенадцать вершин икосаэдра будут лежать на шести гранях куба В икосаэдр может быть вписан тетраэдр, так что четыре вершины тетраэдра будут совмещены с четырьмя вершинами икосаэдра. Икосаэдр можно вписать в додекаэдр, при этом вершины икосаэдра будут совмещены с центрами граней додекаэдра. В икосаэдр можно вписать додекаэдр с совмещением вершин додекаэдра и центров граней икосаэдра. Усечённый икосаэдр может быть получен срезанием 12 вершин с образованием граней в виде правильных пятиугольников. При этом число вершин нового многогранника увеличивается в 5 раз (12×5=60), 20 треугольных граней превращаются в правильные шестиугольники (всего граней становится 20+12=32), а число рёбер возрастает до 30+12×5=90. Собрать модель икосаэдра можно при помощи 20 правильных тетраэдров.

около 428 – 348 г.г. до н.э. около 428 – 348 г.г. до н.э.

Звёздчатые многогранники. Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок. Звёздчатые многогранники. Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Он был открыт Леонардо Да Винчи, затем спустя почти 100 лет переоткрыт И.Кеплером, и назван им "Stella octangula" – звезда восьмиугольная. Отсюда октаэдр имеет и второе название "stella octangula Кеплера". У октаэдра есть только одна звездчатая форма. Её можно рассматривать как соединение двух тетраэдров. Он был открыт Леонардо Да Винчи, затем спустя почти 100 лет переоткрыт И.Кеплером, и назван им "Stella octangula" – звезда восьмиугольная. Отсюда октаэдр имеет и второе название "stella octangula Кеплера". У октаэдра есть только одна звездчатая форма. Её можно рассматривать как соединение двух тетраэдров.

Большой звездчатый додекаэдр принадлежит к семейству тел Кеплера-Пуансо, то есть правильных невыпуклых многогранников. Грани большого звездчатого додекаэдра – пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра. Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г. Это последняя звездчатая форма правильного додекаэдра. Большой звездчатый додекаэдр принадлежит к семейству тел Кеплера-Пуансо, то есть правильных невыпуклых многогранников. Грани большого звездчатого додекаэдра – пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани. Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра. Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г. Это последняя звездчатая форма правильного додекаэдра.

Первая звёздчатая форма икосаэдра. Эту модель делают из 20 частей, каждая часть представляет собой невысокую треугольную пирамиду без основания. Вторая звёздчатая форма икосаэдра. На этой очень красивой модели заметны пятигранные высокие пики, выступающие из впадин модели соединения десяти тетраэдров. Первая звёздчатая форма икосаэдра. Эту модель делают из 20 частей, каждая часть представляет собой невысокую треугольную пирамиду без основания. Вторая звёздчатая форма икосаэдра. На этой очень красивой модели заметны пятигранные высокие пики, выступающие из впадин модели соединения десяти тетраэдров.

Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим. Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Иоганн Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Иоганн Кеплер предположил, что существует связь между пятью правильными многогранниками и шестью открытыми к тому времени планетами Солнечной системы. Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, в который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия. Такая модель Солнечной системы получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.

Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра. Учёным достаточно хорошо изучены правильные выпуклые многогранники, доказано, что существует всего пять видов таких многогранников, но сам ли человек их придумал? Скорее всего – нет, он «подсмотрел» их у природы. Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра. Учёным достаточно хорошо изучены правильные выпуклые многогранники, доказано, что существует всего пять видов таких многогранников, но сам ли человек их придумал? Скорее всего – нет, он «подсмотрел» их у природы.

В 285 году до н.э. на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился в виде трехэтажной башни высотой 120 метров. В основании он был квадратом со стороной тридцать метров, первый 60-метровый этаж башни был сложен из каменных плит и поддерживал 40-метровую восьмигранную башню, облицованную белым мрамором. На третьем этаже, в круглой, обнесенной колоннами башне, вечно горел громадный костер, отражавшийся сложной системой зеркал. В 285 году до н.э. на острове Фарос архитектор Сострат Книдский приступил к строительству маяка. Маяк строился пять лет и получился в виде трехэтажной башни высотой 120 метров. В основании он был квадратом со стороной тридцать метров, первый 60-метровый этаж башни был сложен из каменных плит и поддерживал 40-метровую восьмигранную башню, облицованную белым мрамором. На третьем этаже, в круглой, обнесенной колоннами башне, вечно горел громадный костер, отражавшийся сложной системой зеркал.

Дворец Навуходоносора был построен для его жены Семирамиды на обширной кирпичной площадке, высоко поднимавшейся над окружающей местностью. Пять дворов следовали один за другим с востока на запад, во дворы выходили двери многочисленных комнат. Фасад украшали стройные желтые колонны с голубыми завитками. Окон не было, и свет проникал через три широкие двери. Дворец Навуходоносора был построен для его жены Семирамиды на обширной кирпичной площадке, высоко поднимавшейся над окружающей местностью. Пять дворов следовали один за другим с востока на запад, во дворы выходили двери многочисленных комнат. Фасад украшали стройные желтые колонны с голубыми завитками. Окон не было, и свет проникал через три широкие двери. Висячие сады украшали северо- западную часть дворца. На сводчатых арках из кирпича были расположены террасы, напоминающие уступы гор. Поверх кирпичей залит асфальт, на нем – свинцовые плиты, а на них насыпан слой плодородной земли и посажены деревья, кусты и цветы. Издали кажется, что эти сады как бы висят в воздухе.

Они словно вырастают из песков пустыни - колоссальные, величественные, подавляющие человека необычайными размерами и строгостью очертаний. Стоя у подножия пирамиды, трудно себе представить, что эти огромные каменные горы созданы руками людей. А между тем они были действительно сложены из отдельных каменных глыб, как в наше время дети складывают пирамиды из кубиков. Они словно вырастают из песков пустыни - колоссальные, величественные, подавляющие человека необычайными размерами и строгостью очертаний. Стоя у подножия пирамиды, трудно себе представить, что эти огромные каменные горы созданы руками людей. А между тем они были действительно сложены из отдельных каменных глыб, как в наше время дети складывают пирамиды из кубиков.

Лучшие архитекторы того времени построили мавзолей в виде почти квадратного здания, первый этаж которого был собственно усыпальницей. Снаружи эта громадная погребальная камера, площадью 5000 кв. метров и высотой около 20 метров, была обложена отесанными и отполированными плитами белого мрамора. Во втором этаже, окруженном колоннадой, хранились жертвоприношения, крышей же мавзолея служила пирамида. Лучшие архитекторы того времени построили мавзолей в виде почти квадратного здания, первый этаж которого был собственно усыпальницей. Снаружи эта громадная погребальная камера, площадью 5000 кв. метров и высотой около 20 метров, была обложена отесанными и отполированными плитами белого мрамора. Во втором этаже, окруженном колоннадой, хранились жертвоприношения, крышей же мавзолея служила пирамида.

Скелет одноклеточного организма феодарии по форме напоминает икосаэдр . Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи. Скелет одноклеточного организма феодарии по форме напоминает икосаэдр . Из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.

При производстве алюминия пользуются алюминиево-калиевыми кварцами , монокристалл которых имеет форму правильного октаэдра При производстве алюминия пользуются алюминиево-калиевыми кварцами , монокристалл которых имеет форму правильного октаэдра

В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра. В разных химических реакциях применяется сурьменистый сернокислый натрий – вещество, синтезированное учёными. Кристалл сурьменистого сернокислого натрия имеет форму тетраэдра.

Интересными представители правильных многогранников являются механические головоломки, созданные венгерским преподавателем архитектуры Эрнё Рубиком «Кубик Рубика»(гексаэдр), составленный из 26 кубов, и «Пирамидка Мефферта»(тетраэдр), созданная русским инженером А. А. Ордынцовым. Интересными представители правильных многогранников являются механические головоломки, созданные венгерским преподавателем архитектуры Эрнё Рубиком «Кубик Рубика»(гексаэдр), составленный из 26 кубов, и «Пирамидка Мефферта»(тетраэдр), созданная русским инженером А. А. Ордынцовым.