Презентация на тему: Элементы симметрии правильных многогранников

900igr.net

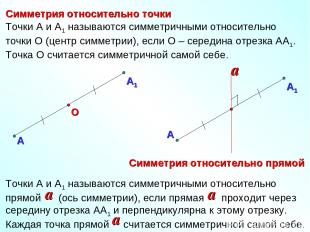
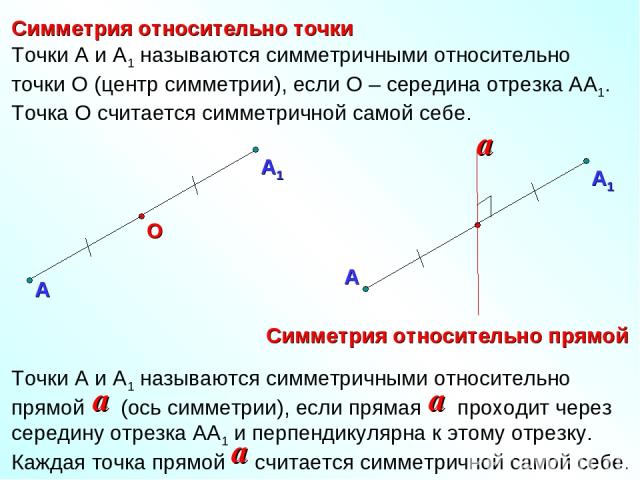
Симметрия относительно точки Симметрия относительно прямой А О Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.

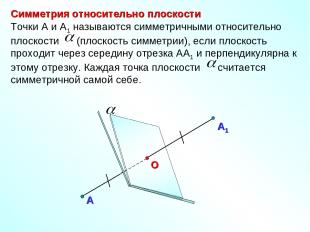
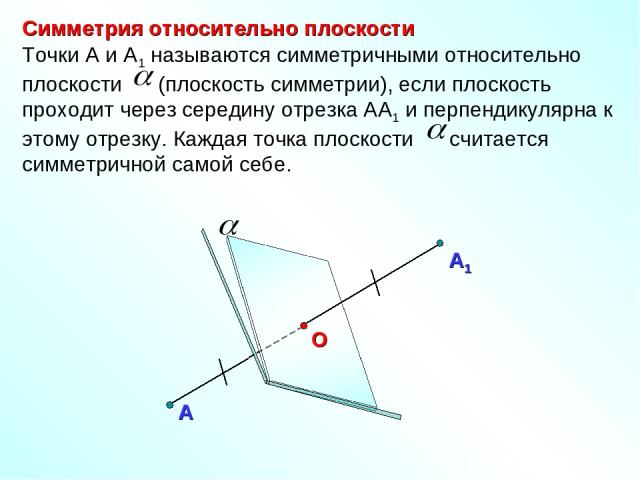
Симметрия относительно плоскости А Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если плоскость проходит через середину отрезка АА1 и перпендикулярна к этому отрезку. Каждая точка плоскости считается симметричной самой себе.

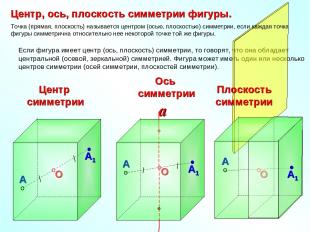
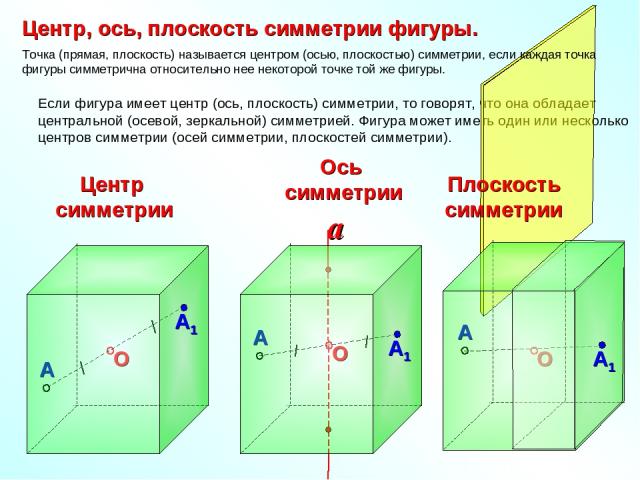
Если фигура имеет центр (ось, плоскость) симметрии, то говорят, что она обладает центральной (осевой, зеркальной) симметрией. Фигура может иметь один или несколько центров симметрии (осей симметрии, плоскостей симметрии). Центр симметрии Плоскость симметрии Точка (прямая, плоскость) называется центром (осью, плоскостью) симметрии, если каждая точка фигуры симметрична относительно нее некоторой точке той же фигуры. Центр, ось, плоскость симметрии фигуры.

С симметрией мы часто встречаемся в архитектуре.

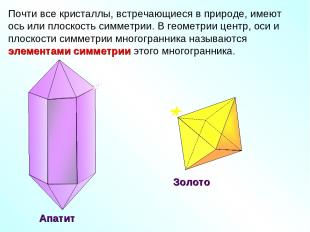
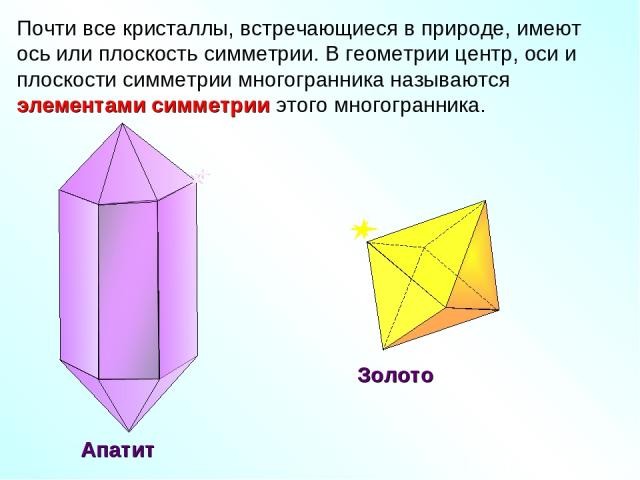
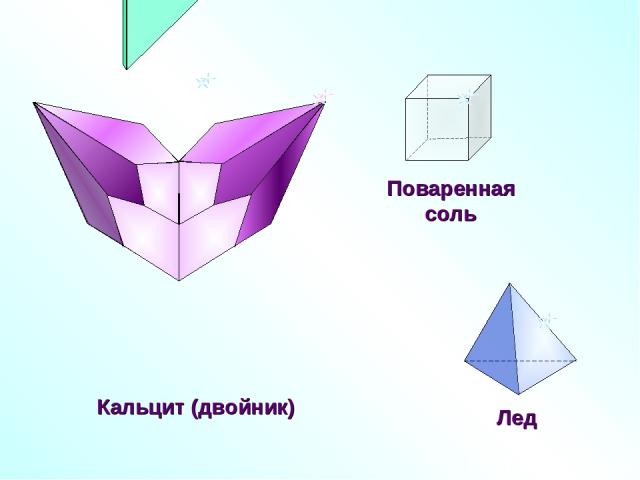
Почти все кристаллы, встречающиеся в природе, имеют ось или плоскость симметрии. В геометрии центр, оси и плоскости симметрии многогранника называются элементами симметрии этого многогранника. Золото

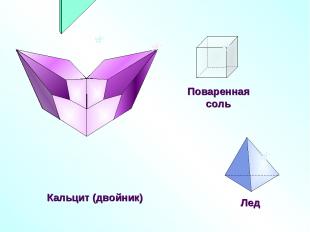
Кальцит (двойник)

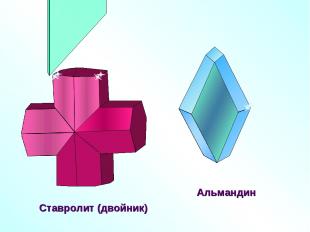
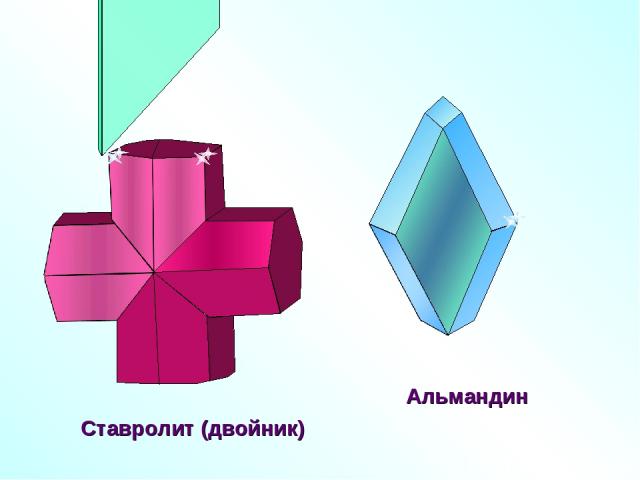
Ставролит (двойник)

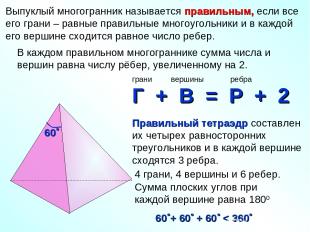
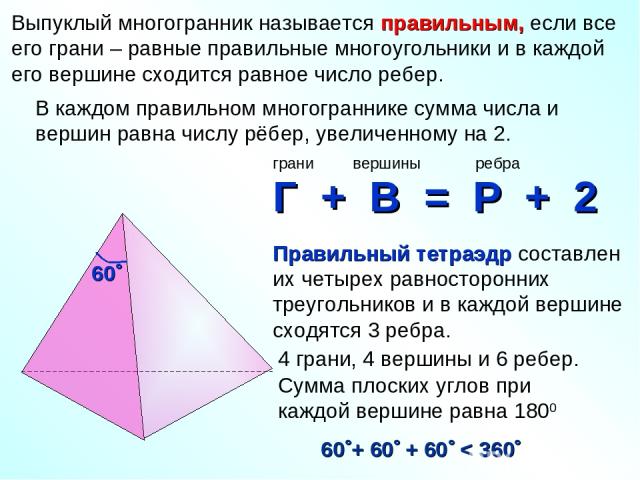
4 грани, 4 вершины и 6 ребер. Сумма плоских углов при каждой вершине равна 1800 Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер. В каждом правильном многограннике сумма числа и вершин равна числу рёбер, увеличенному на 2. 60 + 60 + 60 < 360

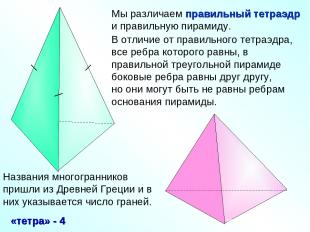
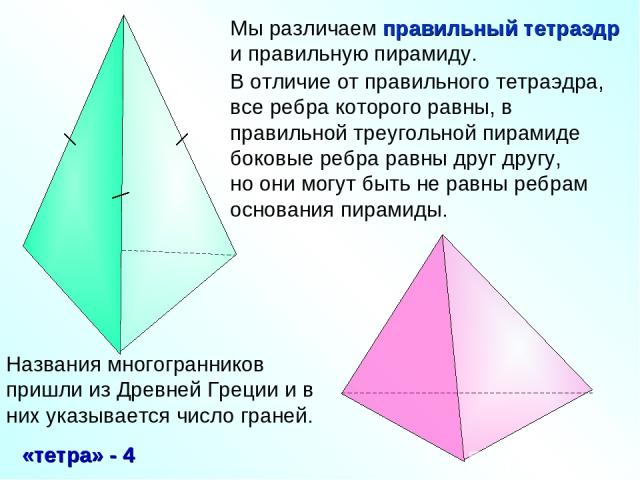
Мы различаем правильный тетраэдр и правильную пирамиду. В отличие от правильного тетраэдра, все ребра которого равны, в правильной треугольной пирамиде боковые ребра равны друг другу, но они могут быть не равны ребрам основания пирамиды.

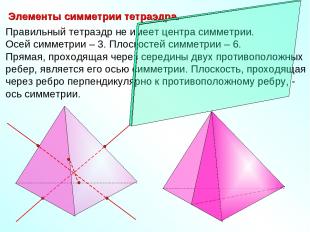
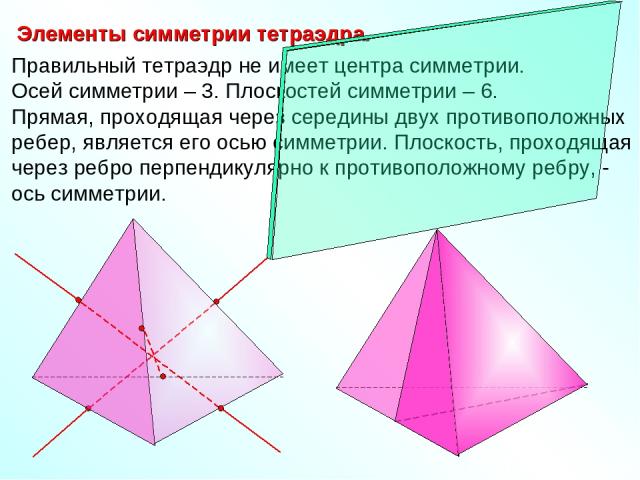
Правильный тетраэдр не имеет центра симметрии. Осей симметрии – 3. Плоскостей симметрии – 6. Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость, проходящая через ребро перпендикулярно к противоположному ребру, - ось симметрии. Элементы симметрии тетраэдра.

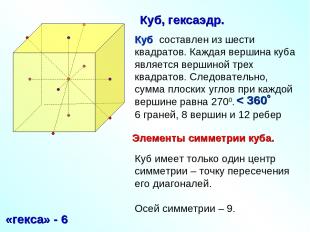
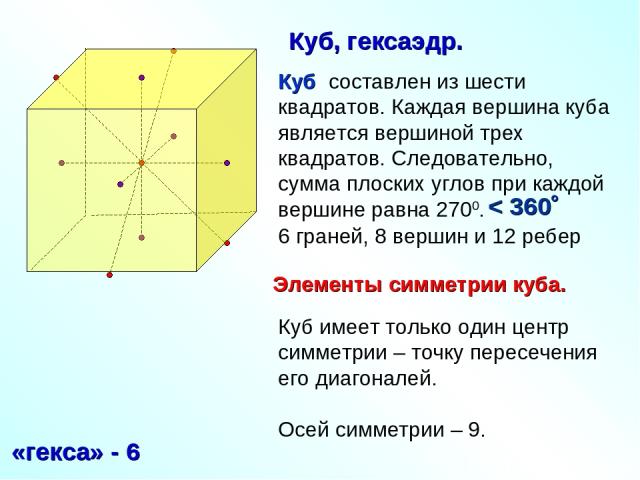
Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 2700. 6 граней, 8 вершин и 12 ребер «гекса» - 6 Куб, гексаэдр. < 360

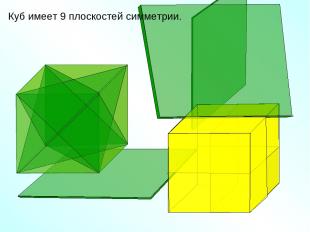
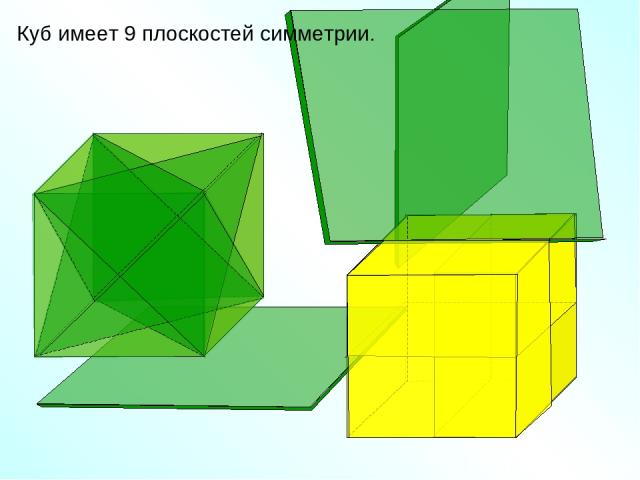
Куб имеет 9 плоскостей симметрии.

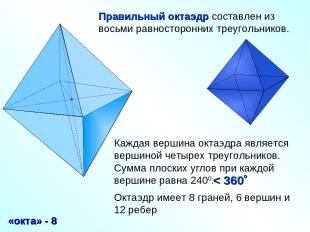
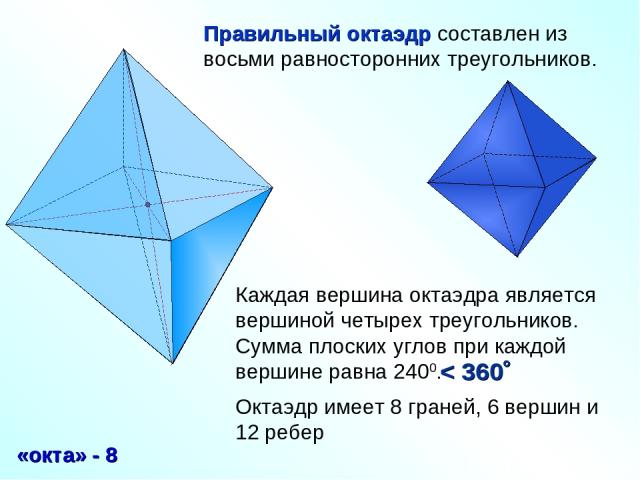
Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Сумма плоских углов при каждой вершине равна 2400. «окта» - 8 Октаэдр имеет 8 граней, 6 вершин и 12 ребер < 360

«икоса» - 20 Икосаэдр имеет 20 граней, 12 вершин и 30 ребер < 360

Правильный додекаэдр составлен из двенадцати правильных шестиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 3240. «додека» - 12 Додекаэдр имеет 12 граней, 20 вершин и 30 ребер. < 360

Первым свойства правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные многогранники называют также телами Платона. Платон 428 – 348 г. до н.э. Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.

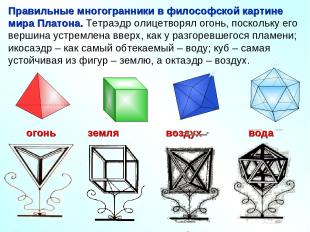
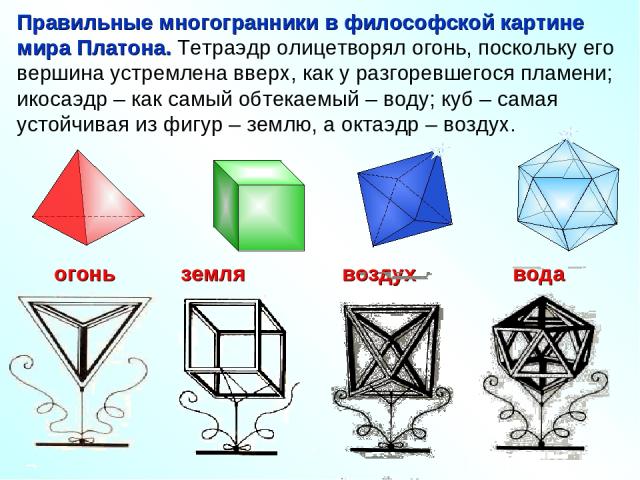
Правильные многогранники в философской картине мира Платона. Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.

Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.

Большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, художники. Их поражало совершенство, гармония многогранников. Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.

Архимед 287 – 212 гг. до н.э. Это многогранники, которые получаются из платоновых тел в результате их  усечения. усечённый тетраэдр, усечённый гексаэдр (куб), усечённый октаэдр, усечённый додекаэдр, усечённый икосаэдр. Архимед описал полуправильные многогранники

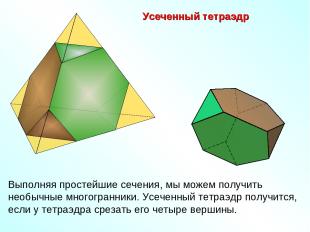
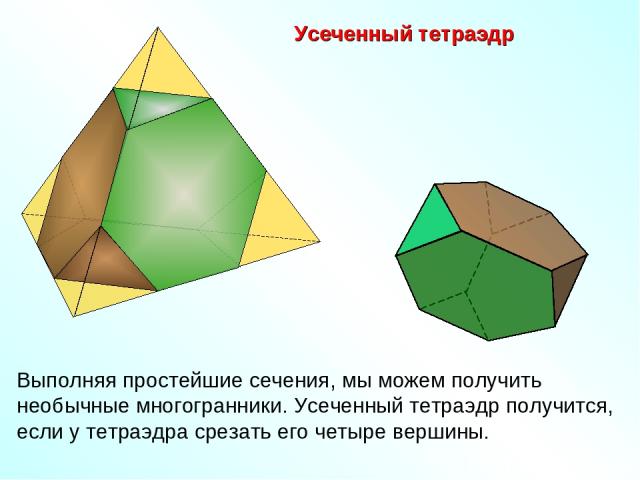
Усеченный тетраэдр Выполняя простейшие сечения, мы можем получить необычные многогранники. Усеченный тетраэдр получится, если у тетраэдра срезать его четыре вершины.

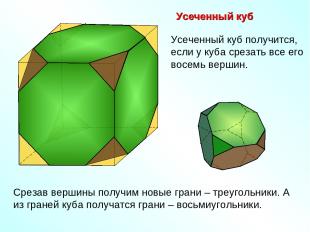
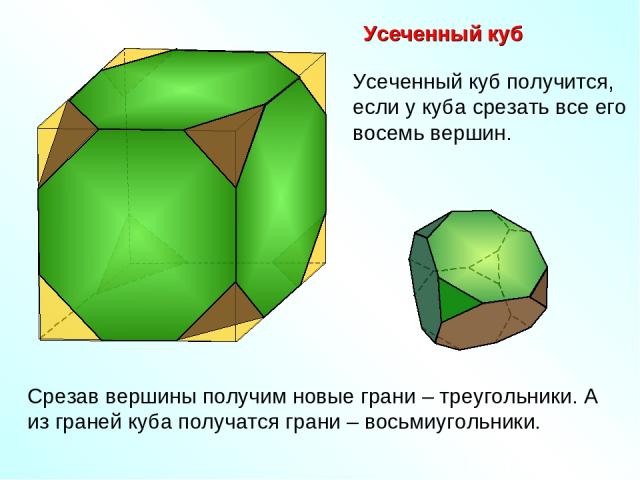
Усеченный куб Срезав вершины получим новые грани – треугольники. А из граней куба получатся грани – восьмиугольники. Усеченный куб получится, если у куба срезать все его восемь вершин.

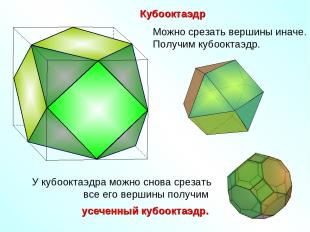
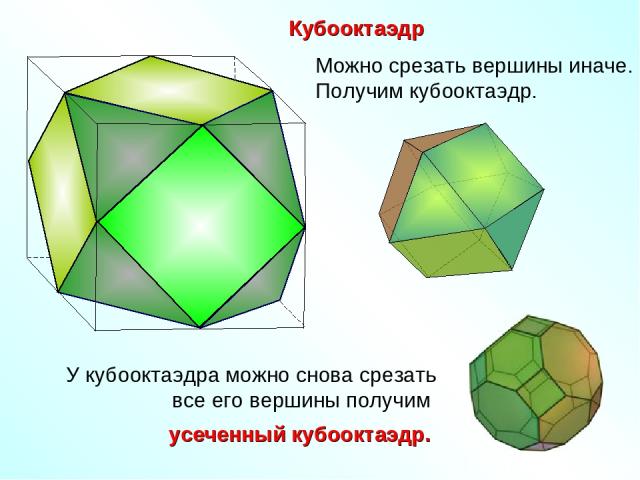
Кубооктаэдр Можно срезать вершины иначе. Получим кубооктаэдр.

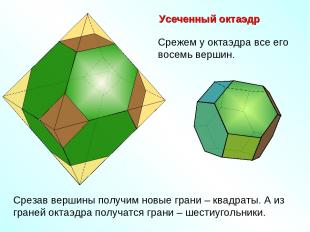
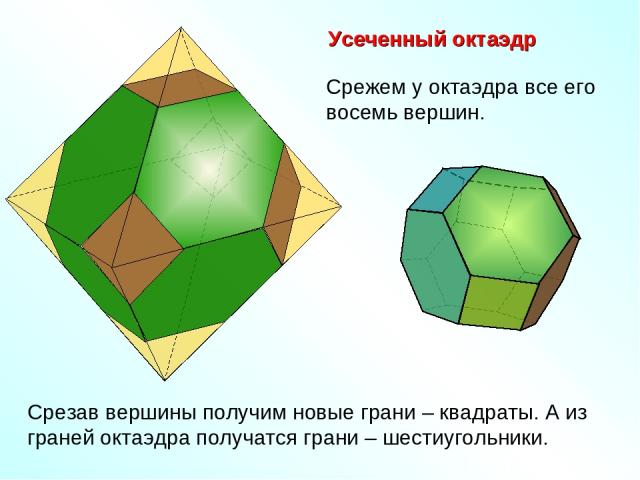
Усеченный октаэдр Срежем у октаэдра все его восемь вершин. Срезав вершины получим новые грани – квадраты. А из граней октаэдра получатся грани – шестиугольники.

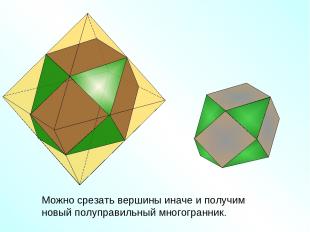
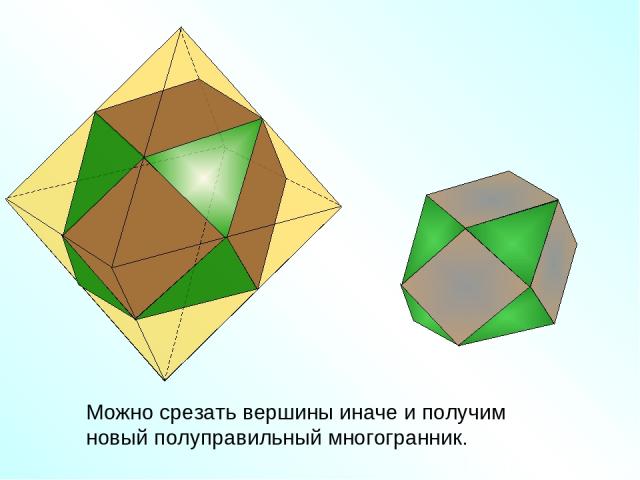
Можно срезать вершины иначе и получим новый полуправильный многогранник.

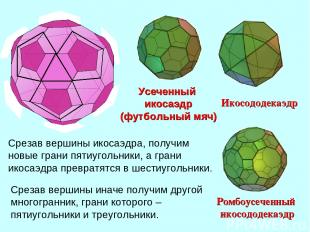
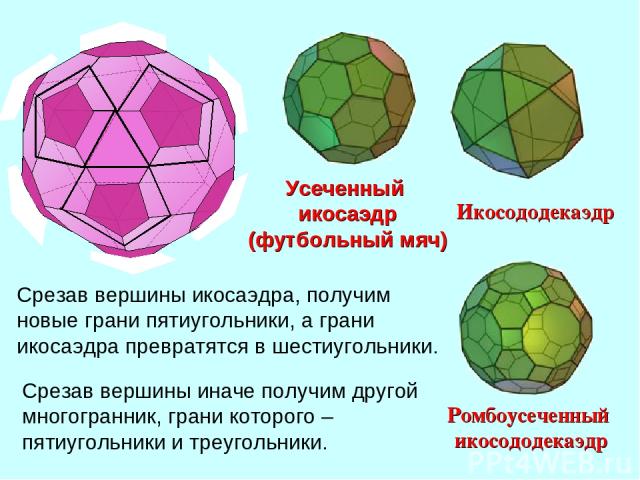
Срезав вершины икосаэдра, получим новые грани пятиугольники, а грани икосаэдра превратятся в шестиугольники. Срезав вершины иначе получим другой многогранник, грани которого – пятиугольники и треугольники.

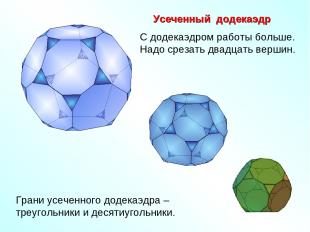
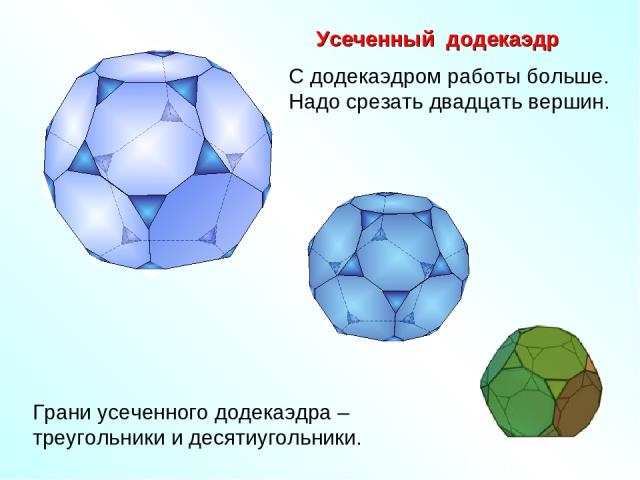
Усеченный додекаэдр С додекаэдром работы больше. Надо срезать двадцать вершин. Грани усеченного додекаэдра – треугольники и десятиугольники.

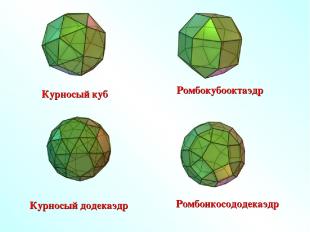
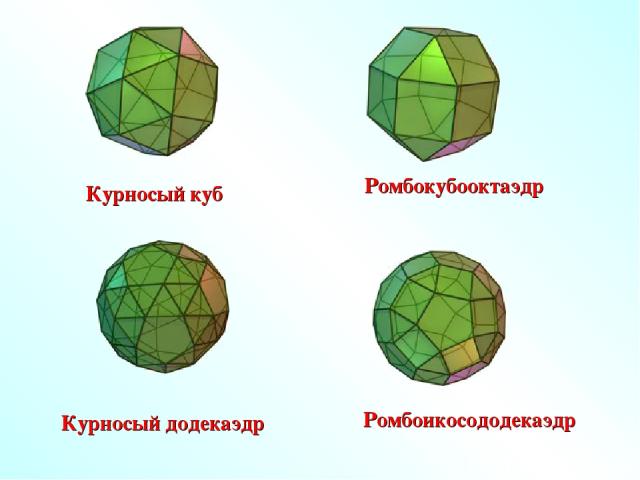
Курносый куб Курносый додекаэдр

Литература. «Геометрия 10-11» Л.С. Атанасян и др. «Детская энциклопедия», том 2. Издательство «Просвещение», Москва 1965. Хотите узнать больше? Посетите сайты. http://ru.wikipedia.org/wiki/%D0%90%D1%80%D1%85%D0%B8%D0%BC%D0%B5%D0%B4%D0%BE%D0%B2%D0%BE_%D1%82%D0%B5%D0%BB%D0%BE http://sharovaeva.narod.ru/ http://pirog13.narod.ru/new_page_5.htm http://www.booksite.ru/fulltext/1/001/008/077/253.htm http://mathworld.wolfram.com/topics/PolyhedronNets.html