Презентация на тему: Правильные многогранники в геометрии


Цели: Знакомить учащихся с новым типом многогранников - правильными многогранниками. Показать влияние правильных многогранников на возникновение филосовских теорий и гипотез. Показать связь геометрии и природы.

«Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд сумел пробраться в самые глубины различных наук» Л.Кэрролл

Как много существует правильных многогранников? Существует всего пять видов таких многогранников. Не существует правильного многогранника, гранями которого являются правильные шестиугольники, семиугольники и, вообще, n-угольники при n≥6.

тетраэдр-огонь

куб-земля

октаэдр-воздух

икосаэдр-вода

додекаэдр-вселенная

С.Дали. Тайная вечеря.
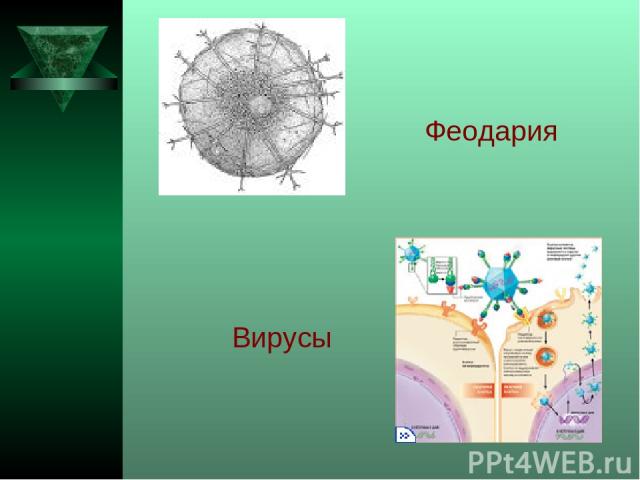
Феодария Вирусы

«Мой дом построен по законам самой строгой архитектуры. Сам Евклид мог бы поучиться, познавая мою геометрию»

Создания природы красивы и симметричны. В кристаллографии существует раздел, который называется «геометрическая кристаллография»

В эпоху Возрождения большой интерес к формам правильных многогранников проявили скульпторы. Знаменитый художник, увлекавшийся геометрией Альбрехт Дюрер (1471- 1528) , в известной гравюре ''Меланхолия '‘ на переднем плане изобразил додекаэдр.

Многогранники в архитектуре. Великая пирамида в Гизе Александрийский маяк

В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана, шотландское озеро Лох-Несс, Бермудский треугольник, Гипотеза В.Макарова и В.Морозова: Ядро Земли имеет форму и свойства растущего кристалла, оказывающего воздействие на развитие всех природных процессов, идущих на планете, Лучи кристалла обуславливают икосаэдро-додекаэрическую структуру Земли, Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки, В местах пересечения рёбер располагаются очаги древних культур и цивилизаций,

Правильные многогранники. Многогранник называется правильным, если все его грани - равные между собой правильные многоугольники и в каждой его вершине сходится одно и то же число граней. Известно только 5 выпуклых правильных многогранников. Правильные выпуклые многогранники следующие: тетраэдр ( 4 грани ); гексаэдр ( 6 граней ) – это хорошо нам известный куб; октаэдр ( 8 граней ); додекаэдр ( 12 граней); икосаэдр ( 20 граней ).

Число вершин, рёбер и граней правильных многогранников связано друг с другом интересным соотношением. Название Тетраэдр Куб Октаэдр Додекаэдр Число граней и их форма 4 6 8 12 Число ребер 6 12 12 30 Число вершин 4 8 6 20

Теорема Эйлера: Число вершин - число ребер + число граней =2 Один из величайших математиков мира, работы которого оказали решающее влияние на развитие многих современных разделов математики. Л.Эйлер (1707-1783)