Презентация на тему: Перпендикулярность в пространстве (10 класс)

МОУ СОШ № 7Интеллектуальный марафон по геометрии Перпендикулярностьв пространствеПодготовила:Ученица 10 класса «б»Лаврова ДарьяУчитель: Архипова Елена Сергеевна

Перпендикулярностьв жизни

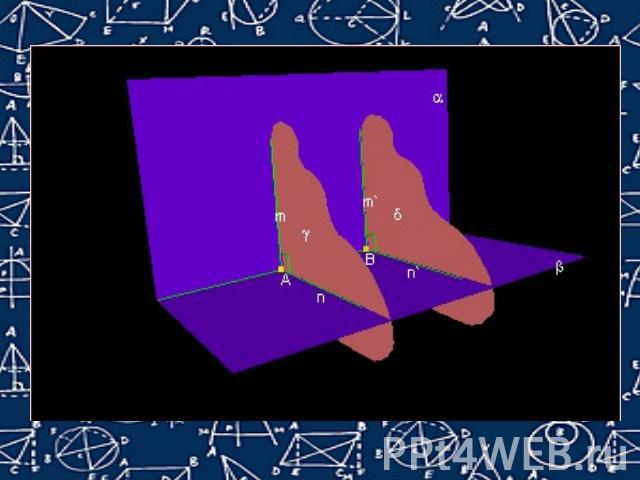
Перпендикулярность вплоскостях

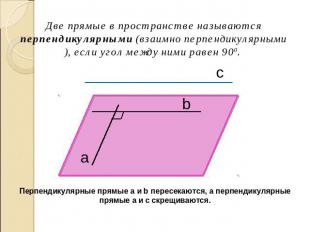
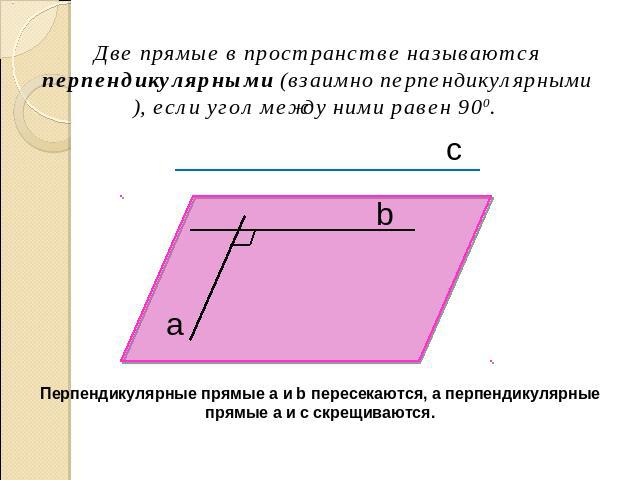
Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 900. Перпендикулярные прямые a и b пересекаются, а перпендикулярные прямые a и c скрещиваются.

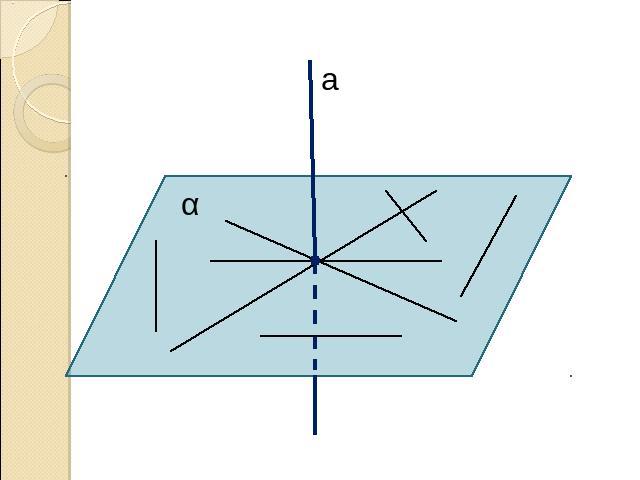
Параллельные прямые, перпендикулярные к плоскостиПрямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

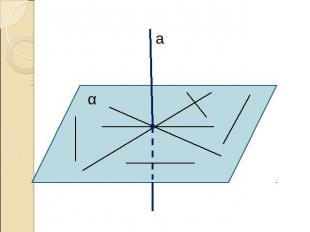
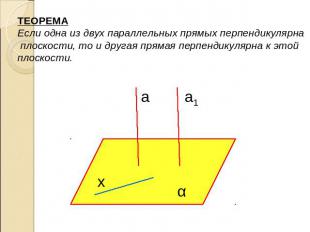
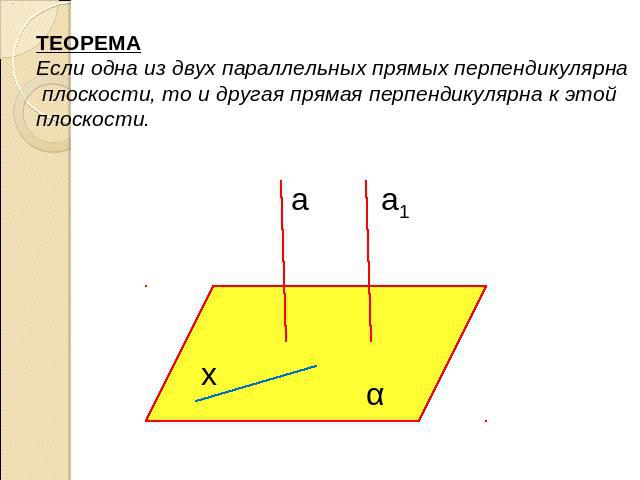
ТЕОРЕМАЕсли одна из двух параллельных прямых перпендикулярна плоскости, то и другая прямая перпендикулярна к этой плоскости.

ТЕОРЕМАЕсли две прямые перпендикулярны к плоскости, то они параллельны.

Признак перпендикулярности прямой и плоскости

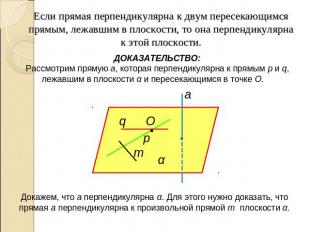
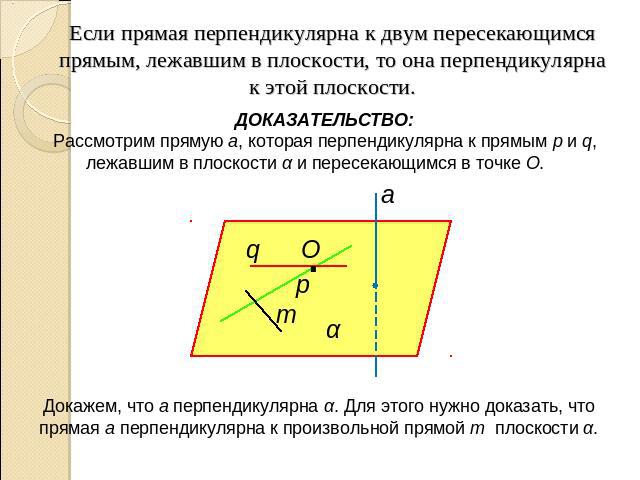
Если прямая перпендикулярна к двум пересекающимся прямым, лежавшим в плоскости, то она перпендикулярна к этой плоскости.ДОКАЗАТЕЛЬСТВО:Рассмотрим прямую a, которая перпендикулярна к прямым p и q, лежавшим в плоскости α и пересекающимся в точке О. Докажем, что a перпендикулярна α. Для этого нужно доказать, что прямая a перпендикулярна к произвольной прямой m плоскости α.

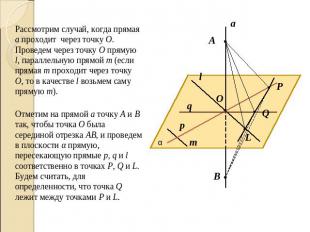
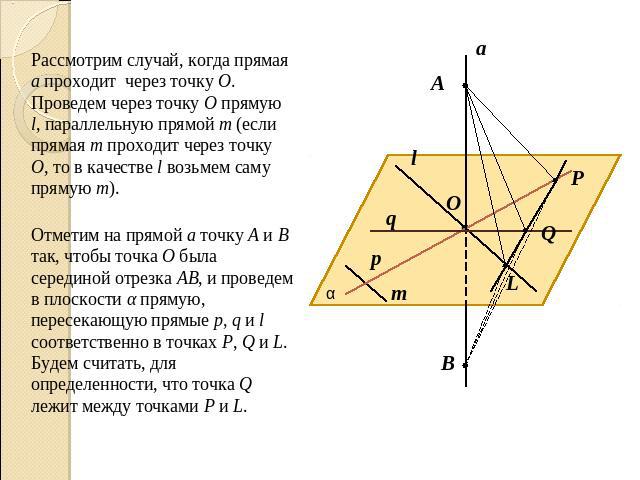
Рассмотрим случай, когда прямая а проходит через точку О. Проведем через точку О прямую l, параллельную прямой m (если прямая m проходит через точку О, то в качестве l возьмем саму прямую m).Отметим на прямой а точку А и В так, чтобы точка О была серединой отрезка АВ, и проведем в плоскости α прямую, пересекающую прямые p, q и l соответственно в точках P, Q и L.Будем считать, для определенности, что точка Q лежит между точками P и L.

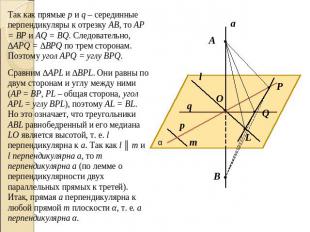
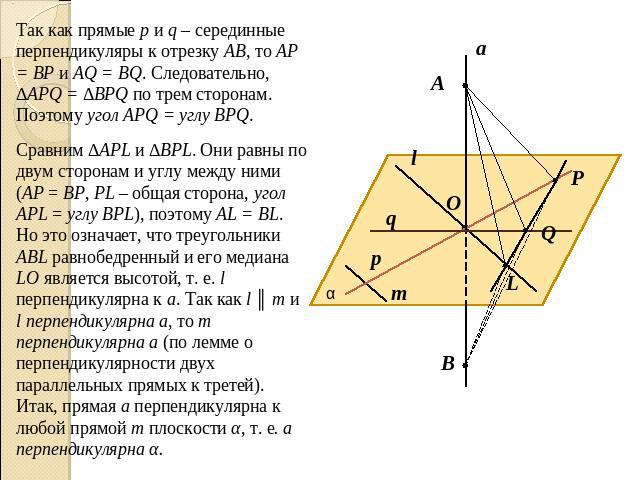
Так как прямые p и q – серединные перпендикуляры к отрезку АВ, то АР = ВР и AQ = BQ. Следовательно, ∆APQ = ∆BPQ по трем сторонам. Поэтому угол APQ = углу BPQ.Сравним ∆APL и ∆BPL. Они равны по двум сторонам и углу между ними (AP = BP, PL – общая сторона, угол APL = углу BPL), поэтому AL = BL. Но это означает, что треугольники ABL равнобедренный и его медиана LO является высотой, т. е. l перпендикулярна к а. Так как l ║ m и l перпендикулярна а, то m перпендикулярна а (по лемме о перпендикулярности двух параллельных прямых к третей). Итак, прямая а перпендикулярна к любой прямой m плоскости α, т. е. а перпендикулярна α.

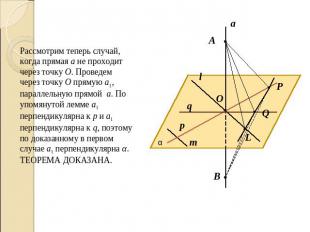
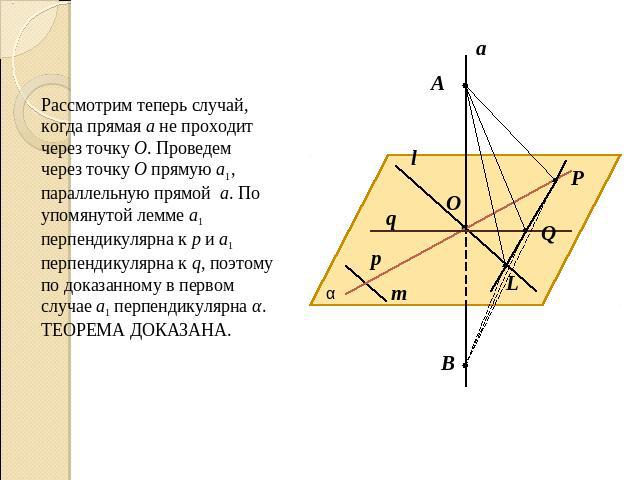
Рассмотрим теперь случай, когда прямая а не проходит через точку О. Проведем через точку О прямую а1, параллельную прямой а. По упомянутой лемме а1 перпендикулярна к р и а1 перпендикулярна к q, поэтому по доказанному в первом случае а1 перпендикулярна α.ТЕОРЕМА ДОКАЗАНА.