Презентация на тему: Аналитическая геометрия

Математика Лекция 5

Аналитическая геометрия

Алгебраические поверхности и линии на плоскости первого порядка Опр. Геометрическое место точек в пространстве (на плоскости) определяет плоскость (прямую на плоскости) тогда и только тогда, когда декартовы координаты x, y, z текущей точки М удовлетворяют алгебраическому уравнению первого порядка


Геометрический смысл нормального вектора Задача 1. На плоскости дана точка и вектор . Составить уравнение прямой на плоскости, проходящей через точку перпендикулярно вектору.Рассмотрим текущую точку прямой тогда вектор лежит на данной прямой.

Нормальный вектор – вектор, перпендикулярный прямой.

Задача 2. В пространстве дана точка и вектор . Составить уравнение плоскости, проходящей через точку перпендикулярно вектору. Рассмотрим текущую точку прямой вектор лежит на плоскости.

Нормальный вектор – вектор, перпендикулярный плоскости.
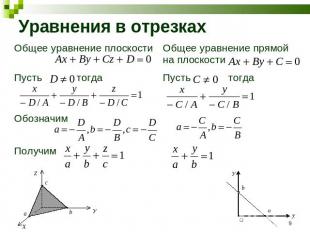
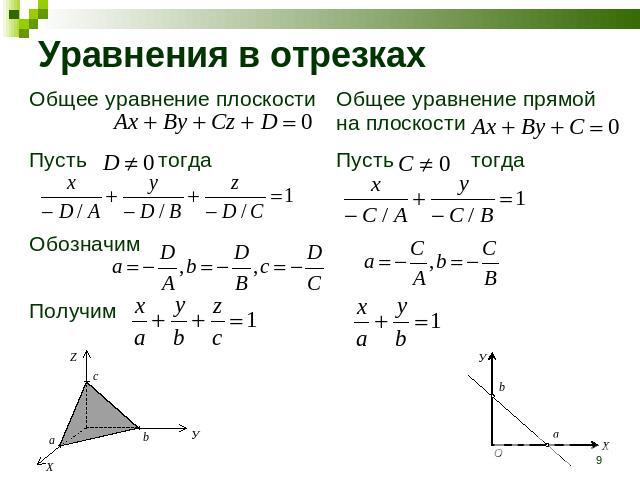
Уравнения в отрезках

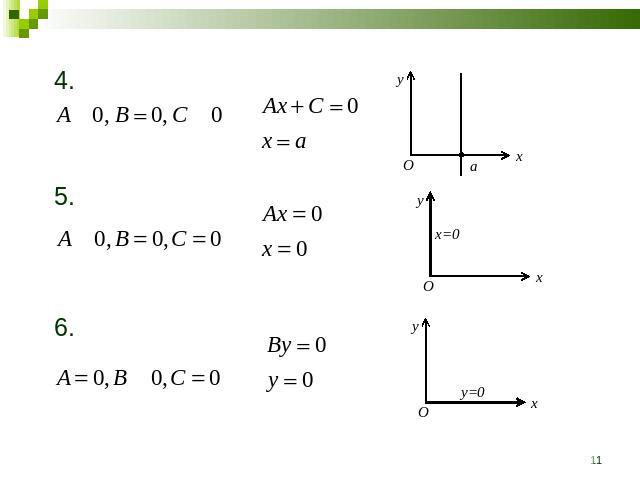
Исследование уравнения прямой

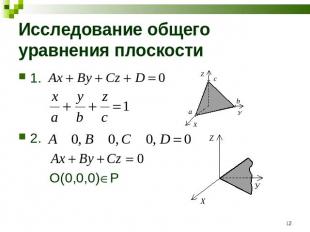
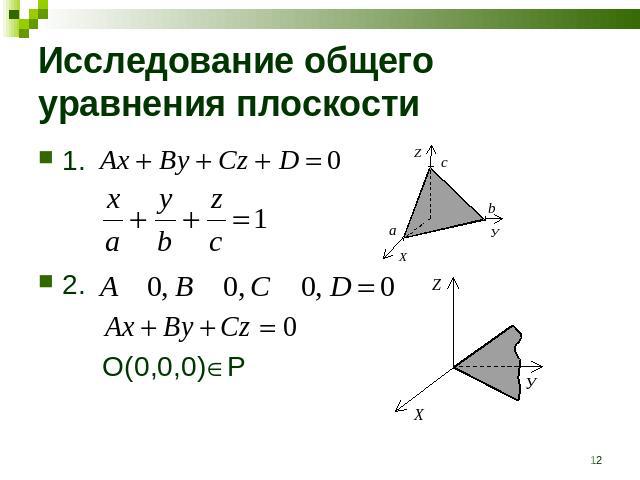
Исследование общего уравнения плоскости
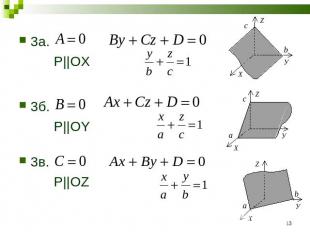

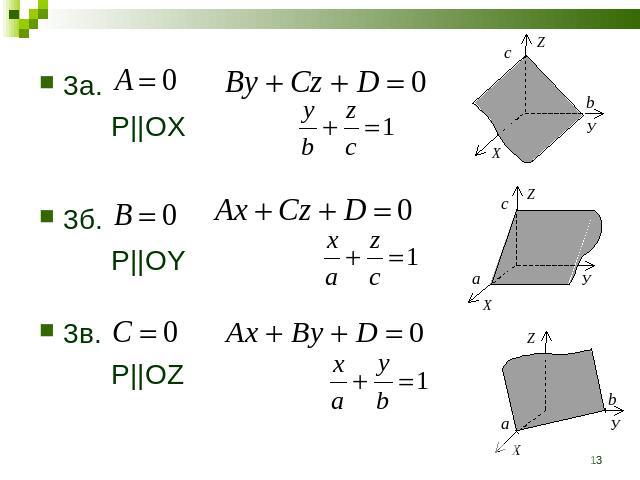
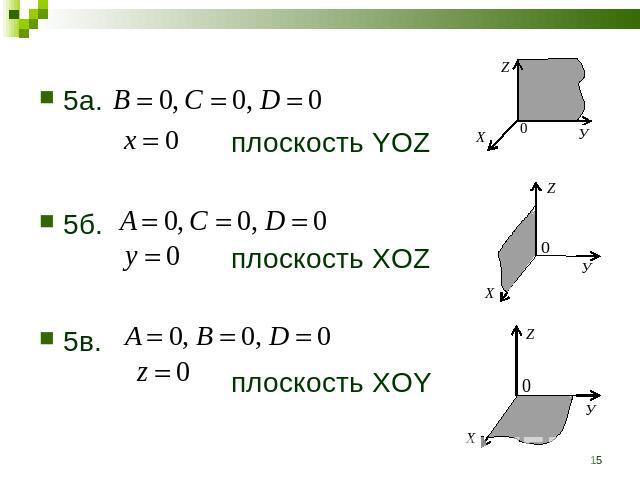
4а.4а. P||XOY4б. P||XOZ4в. P||YOZ
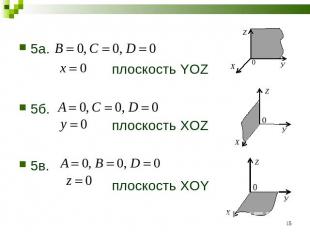
5а.5а. плоскость YOZ5б. плоскость XOZ5в. плоскость XOY
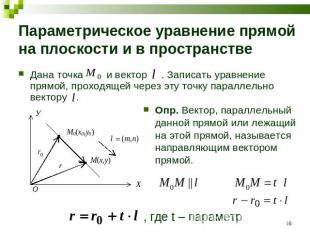
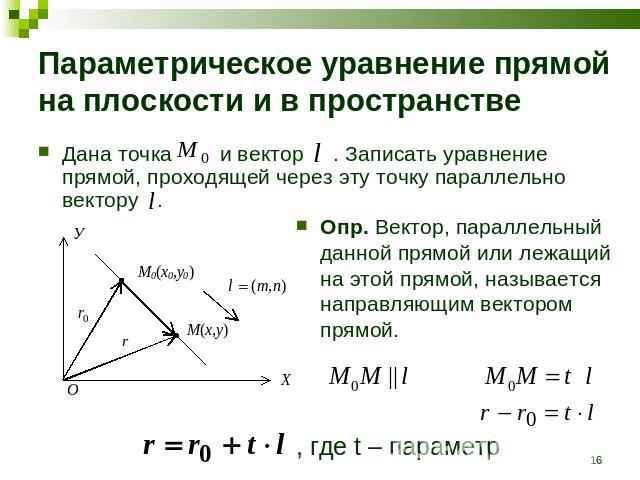
Параметрическое уравнение прямой на плоскости и в пространстве Дана точка и вектор . Записать уравнение прямой, проходящей через эту точку параллельно вектору . Опр. Вектор, параллельный данной прямой или лежащий на этой прямой, называется направляющим вектором прямой. , где t – параметр


Если исключить параметр t из параметрического уравнения, то получим каноническое уравнение прямой.Если исключить параметр t из параметрического уравнения, то получим каноническое уравнение прямой.

Уравнение прямой проходящей через две точки М1 и М2

Параметрическое уравнение плоскости Дана точка и два неколлинеарных вектора Составить уравнение плоскости, проходящей через точку параллельно векторам . Векторы компланарны, линейно зависимы один из них является линейной комбинацией остальных, т.е.p, q – параметрыили

Уравнение плоскости, проходящей через точку параллельно двум векторам

Уравнение плоскости, проходящей через три точки Векторы компланарны