Презентация на тему: Производные тригонометрических функций (10 класс)

Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа № 12 с углубленным изучением отдельных предметов» Тема урока: «Производные тригонометрических функций» Автор: учитель математики Гулова Римма Ивановна г.Старый Оскол 2011г.

Цели урока: Ввести формулы производных тригонометрических функций рассмотреть методы решения упражнений на применение изученных правил дифференцирования; вырабатывать умения и навыки учащихся в решении заданий на применение знаний правил вычисления производных тригонометрических функций. Воспитание и развитие логического мышления учащихся.

План урока 1.Орг. момент. 2.Актуализация опорных знаний учащихся. 3.Изучение нового материала. 3.1.Формула производной синуса 3.2.Формулы дифференцирования косинуса, тангенса и котангенса. 4.Закрепление изученного материала: 4.1. Работа у доски и на местах. Решение упражнений из учебника . 4.2.Работа в группах. 5.Подведение итогов урока. 6.Домашнее задание.

Актуализация опорных знаний учащихся: Написать на доске чему равна производная: числа переменной «х» выражения kx + b суммы функций произведения двух функций частного двух выражений степенной функции сложной функции

Формулы вычисления производных

1)Формула производной синуса Докажем, что производная синуса имеет такой вид:

Вспомним определение производной:

Воспользуемся формулой суммы и разности тригонометрических функций :

Для вывода формулы производной синуса достаточно показать, что:

Действительно, опираясь на эти утверждения, при Δх → 0 можно получить формулу:

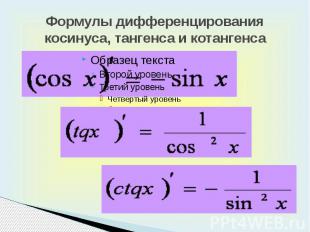
Формулы дифференцирования косинуса, тангенса и котангенса

Работа в группах: Найти производные данных функций

Подведение итогов урока Что чувствовали сегодня на уроке? С какими трудностями вы встретились? Кому было трудно? Почему? Что ты сделал, чтобы преодолеть эту трудность? Что тебе помогло? (Опорные конспекты, подсказки товарищей…)

Домашнее задание: Пункт 17 , № 235, 236 (а, б).

Литература: Алгебра и начала математического анализа: учеб. для 10—11 кл. общеобразоват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын и др.; под. ред. А. Н. Колмогорова. — М.: Просвеще ние, 2008.   Дидактические материалы по алгебре и началам анализа для 10 класса / Б. М. Ивлев, С. М. Саакян, С. И. Шварцбурд. - М.: Просвещение, 2008.