Презентация на тему: Производные функций

= 900igr.net По геометрическому смыслупроизводной, значение производной функцииf(x)= вточке х0= 0 равно tg450= 1. Таким образом,f’(0) ==1. План нахожденияпроизводнойфункцииf(x) =. 1.Находим приращение функции ∆f: ∆f= 2.Вычислим отношение приращения функции к приращению аргумента= 1=при∆х→0. Тогда по определению производной получаем: у’ =или любом прих.

. · По основному логарифмическому тождеству х = при всех положительных х, т.е. в этом равенстве справа и слева стоит одна и та же функция, определенная на R+ . Поэтому производные Х и равны. = . = 1 . Производную правой части вычисляем по правилу нахождения сложной функции · = х· Имеем 1 = х· (lnx)’ = =

1. Найдите числовое значение: Основноелогарифмическое тождество =N,N˃0,a˃ 0,a≠ 1.

2. Представьте в виде степени с основанием е: 4 6 а

а 8 Основное логарифмическое тождество = N,N˃0, a˃ 0, a ≠ 1. 1. Найдите числовое значение: 2 Представьтев виде степени с основаниеме: 4

Найдем производные полученных функций: = · = ; = · = ; = · = . = .

Формула перехода от одного основаниялогарифмак другому Найти производную:а)= = = ; б) = = = ; в)= = = . =

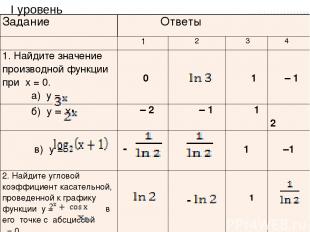
I уровень Задание Ответы 1 2 3 4 1. Найдите значение производной функции прих= 0. а) у = 0 1 – 1 б) у=х· – 2 – 1 1 2 в) у = - 1 –1 2. Найдите угловой коэффициент касательной, проведенной к графику функции у =веготочке с абсциссой=0. - 1

( II уровень. 1. Найдите значение ( , если = 1) ; 2) ; 3) ; 4) 2. Найдите тангенс угла наклона касательной, проведенной к графику функции у = в его точке с абсциссой = 0. Ответ :_____________ убывает на D(y). 3. Докажите, что функция у =

I уровень Найдитезначение производной функции прих= 0. а) у =. Решение.=ƒ’(0) == .Ответ: 2. б) у =х·Решение. (х·’=х’·+x·=+x·.ƒ’(0) =+0·=1.Ответ:3. в) у =.Решение. =. ƒ’(0)= = .Ответ: 2. 2. Найдите угловой коэффициент касательной, проведенной к графику функции у =вего точке сабсциссой= 0. Решение. Так как угловой коэффициент касательной равенƒ’(х0).Найдем производную функции: ƒ’(х) == – .K=ƒ’(0)= – = .Ответ: 1.

IIуровень 1. Найдите значение (, если = . . Решение.(х)===. (==.Ответ: 1. 2. Найдите тангенс угла наклона касательной, проведенной кграфику функцииу =в его точке с абсциссой= 0. Решение. Так как тангенс угла наклона касательной равенƒ’(х0).Найдем производную функции: = ()’ =. tgα===. Ответ:. 3. Докажите, что функция у =)убывает на D(y). Решение. Область определения данной функции промежуток(); (х= 0на интервале(),следовательно,функция у= )убывает на D(y).