Презентация на тему: Принцип Дирихле

900igr.net

Дирихле родился в городе Дюрен в семье почтмейстера.  В 12 лет Дирихле начал учиться в гимназии в Бонне, спустя два года в иезуитской гимназии в Кёльне, где в числе прочих преподавателей его учил Георг Ом. В 1855 г. Дирихле становится профессором высшей математики в Гёттингенском университете.

Традиционная формулировка звучит так: «Если в n клетках сидит n+1 или больше зайцев, то найдётся клетка, в которой сидят по крайней мере два зайца» Но существуют еще две формулировки: "При любом отображении множества P, содержащего n+1 элементов, в множество Q, содержащее n элементов, найдутся два элемента множества P, имеющие один и тот же образ» "Если nk+1 зайцев размещены в n клетках, то найдутся k+1 зайцев, которые посажены в одну клетку (n, k - натуральные числа)".

Один математик сказал, что Дирихле по частоте упоминаний ученикам навсегда обеспечено одно из самых высших мест. И добавил: "Пожалуй, есть способ лишить его лидерства — назвать чьим-нибудь именем принцип «никакое чётное число не равно никакому нечётному». Несмотря на очевидность этого принципа и, казалось бы простоту, с его помощью в решении ,многие сложные задачи сводятся к простому и эффективному решению. Принцип Дирихле даёт только неконструктивное доказательство - мы не можем сказать, в какой именно клетке сидят два зайца, а знаем только, что такая клетка есть. Зачастую вся сложность применения принципа Дирихле состоит в том чтобы определить , что считать «зайцем», что – «клеткой».

На шахматной доске стоят 44 ферзя. Докажите, что каждый из них бьёт какого-нибудь другого ферзя.

При любом положении на доске ферзь бьёт не менее 21 поля. Пусть какой-то из этих 44 ферзей не бьёт никакого другого ферзя. Тогда все клетки, которые находятся под боем этого ферзя, пусты. А так как при любом положении на шахматной доске ферзь бьёт не менее 21 поля, то занято ферзями не более 64 – 21 = 43 полей.

Внутри равностороннего треугольника со стороной 1 расположено 5 точек. Доказать, что расстояние между некоторыми двумя из них меньше 0,5.

Проведем средние линии треугольника. Они разобьют его на четыре правильных треугольника со стороной 0,5. По принципу Дирихле из пяти точек хотя бы две окажутся в одном из четырёх треугольников. Используем лемму о том, что длина отрезка, расположенного внутри треугольника, меньше длины его наибольшей стороны. Расстояние между этими точками меньше 0.5 так как точки не лежат в вершинах треугольников.

Дано 11 различных целых чисел. Доказать, что из них можно выбрать два числа, разность которых делится на 10.

При помощи принципа Дирихле определим что по крайней мере два числа из доступных 11 имеют одинаковый остаток при делении их на 10. Пусть это будут числа Z = 10z + r и F = 10f + r. (Буквой r означим остаток при делении этих чисел). Тогда их разность делится на 10: Z - F = 10(z - f).

Доказать, что если имеется 100 целых чисел x1, x2, . . . , x100, то из них можно выбрать несколько чисел, сумма которых делится на 100.

Рассмотрим 100 следующих сумм: 1)S1= x1  2)S2 = x1 + x2 И т.д. вплоть до:  100)S100=x1+x2+ x3+. . .+ x100. Если хотя бы одна из этих сумм делится на 100 то задача решена. Допустим, что ни одно из чисел S1, S2, . . . , S100 не делится на 100. По принципу Дирихле, два из них при делении на 100 дают равные остатки (т. к. «кроликов» у нас 100, а «клеток»может быть лишь 99). Пусть это SZ и SF (Z < F). Тогда разность SF-SZ= (x1 +. . .+ xF) - (x1 +. . .+ xZ) = xZ + 1+. . .+ xF делится на 100, и поэтому сумма x Z+ 1+. . .+ xF является искомой.

"Если внутри множества меры V расположено несколько множеств, сумма мер которых больше V, то найдётся общий элемент, принадлежащий по крайней мере двум из этих множеств". Для длин и площадей это положение формулируется так: "Если на отрезке длины L расположено несколько отрезков с суммой длин больше L, то хотя бы два из них имеют общую точку"; "Если внутри фигуры площади S находится несколько фигур, имеющих сумму площадей больше S, то хотя бы две из них имеют общую точку".

На отрезке длиной 1 расположены попарно не пересекающиеся отрезки, сумма длин которых равна p. Обозначим эту систему отрезков A. Пусть B — дополнительная система отрезков (отрезки систем A и B не имеют общих внутренних точек и полностью покрывают данный отрезок). Докажите, что существует параллельный перенос T, для которого пересечение B и T(A) состоит из отрезков, сумма длин которых не меньше p(1 - p)/2. 

Пусть с от -1 до 1. Сдвинем данный отрезок на c вдоль себя, а затем сдвинем его на c в ортогональном направлении. Заштрихованная на рис. область соответствует пересечению отрезков Ai и Bj. Ее площадь равна произведению длин этих отрезков. Если рассмотреть все пары отрезков систем A и B, то заштрихованная область будет иметь площадь p(1 - p). Поэтому некоторое горизонтальное сечение заштрихованных областей имеет длину не меньше p(1 - p)/2.  Замечание. Если вместо отрезка рассматривать окружность (и вместо параллельного переноса поворот), то p(1 - p)/2 можно заменить на p(1 - p). 

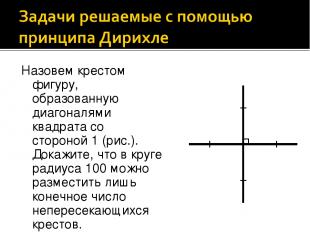
Назовем крестом фигуру, образованную диагоналями квадрата со стороной 1 (рис.). Докажите, что в круге радиуса 100 можно разместить лишь конечное число непересекающихся крестов.

Для каждого креста рассмотрим круг радиусом 1/2 с центром в центре креста. Докажем, что если пересекаются два таких круга, то пересекаются и сами кресты. Расстояние между центрами пересекающихся равных кругов не превосходит их удвоенного радиуса, поэтому расстояние между центрами соответствующих им крестов не превосходит 1/. Рассмотрим прямоугольник. заданный перекладинами первого креста и центром второго (рис.). Одна из перекладин второго креста проходит через этот прямоугольник, поэтому она пересекает первый крест, так как длина перекладины равна 1/, а длина диагонали прямоугольника не превосходит 1/. В круге конечного радиуса можно разместить лишь конечное число непересекающихся кругов радиуса 1/2

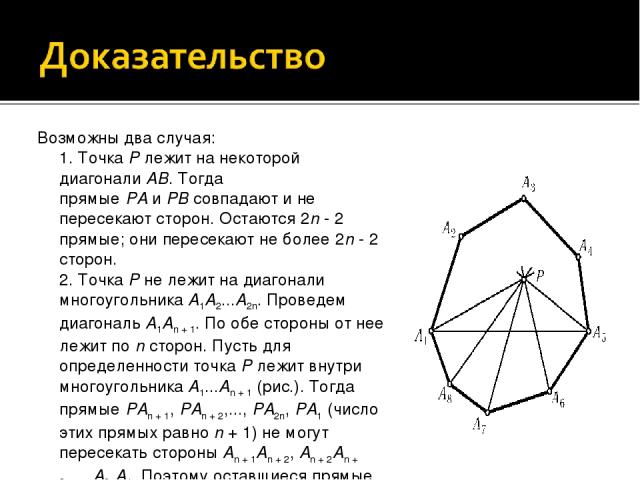
Внутри выпуклого 2n-угольника взята точка P. Через каждую вершину и точку P проведена прямая. Докажите, что найдется сторона 2n-угольника, с которой ни одна из проведенных прямых не имеет общих внутренних точек. 

Возможны два случая:  1. Точка P лежит на некоторой диагонали AB. Тогда прямые PA и PB совпадают и не пересекают сторон. Остаются 2n - 2 прямые; они пересекают не более 2n - 2 сторон.  2. Точка P не лежит на диагонали многоугольника A1A2...A2n. Проведем диагональ A1An + 1. По обе стороны от нее лежит по n сторон. Пусть для определенности точка P лежит внутри многоугольника A1...An + 1 (рис.). Тогда прямые PAn + 1, PAn + 2,..., PA2n, PA1 (число этих прямых равно n + 1) не могут пересекать стороны An + 1An + 2, An + 2An + 3,..., A2nA1. Поэтому оставшиеся прямые могут пересекать не более чем n - 1 из этих n сторон.