Презентация на тему: Процентные вычисления в жизненных ситуациях

Процентные вычисления в жизненных ситуациях

Цель данной работы:Рассмотреть основные типы задач на процентыПоказать широту применения задач «на проценты»Выявить сферы применения данных задачРассмотреть формулу сложного процента, а также схему расчета сложного процента и их применение при решении задач на проценты

Задачи данной работы:Провести анализ математической и научно-методической литературы по проблеме исследования с целью выделения основных теоретических фактов по теме «Проценты».Выяснить историю происхождения процента, выделить основные типы задач по теме «Проценты».Выяснить сферы использования процентов, их роль в жизни человека.Рассмотреть основные типы задач «на проценты» с их последующим решением, выделить формулу для вычисления «сложного процента», а также схему решения задач на «сложные проценты».

История создания процентов. Само слово «процент» происходит от лат. «pro centum», что означает в переводе «сотая доля». В 1685 году в Париже была издана книга «Руководство по коммерческой арифметике» Матье де ла Порта. В одном месте речь шла о процентах, которые тогда обозначали «cto» (сокращенно от cento). Однако наборщик принял это «cto» за дробь и напечатал «%». Так из-за опечатки этот знак вошёл в обиход. Были известны проценты и в Индии. Индийские математики вычислили проценты, применяя так называемое тройное правило, то есть пользуясь пропорцией. В Древнем Риме были широко распространены денежные расчеты с процентами. Римский сенат установил максимально доступный процент, взимавшийся с должника.

В Европе в средние века расширилась торговля и, следовательно, особое внимание обращалось на умение вычислять проценты. Тогда приходилось рассчитывать не только проценты, но и проценты с процентов (сложные проценты). Часто конторы и предприятия для облегчения расчетов разрабатывали особые таблицы вычисления процентов. Эти таблицы держались в тайне, составляли коммерческий секрет фирмы. Впервые таблицы были опубликованы в 1584 году Симоном Стевином. Фламандский ученый, военный инженер Симон Стевин не был по профессии математиком, но его трудолюбие и талант позволили ему занять достойное место среди выдающихся европейских математиков. Он первым в Европе открыл десятичные дроби. Симон Стевин опубликовал таблицу для вычисления сложных процентов, которая использовалась в торгово-финансовых операциях. В практической жизни полезно знать связь между простейшими значениями процентов и соответствующими дробями: половина - 50% , четверть - 25% , три четверти - 75% , пятая часть - 20% , три пятых - 60% и т.д.

Основные теоретические факты: В любой задачи есть условие, т.е. исходныеданные, заключение, т.е. требование, котороенужно выполнить и субъект, который этотребование выполнит. Задача – это задание, которое должен выполнить субъект, или вопрос, на который он должен найти ответ, опираясь на указанное условие и все вытекающие из них следствия.

Основные методы решения текстовых задач:Арифметический - Суть арифметического метода состоит в том, что задачи решаются по действиям.Алгебраический - Суть алгебраического метода решения задач состоит в том, что одна из величин принимается, например за х, все зависимости существующие между величинами переводятся на язык равенств, уравнений и далее решается полученное уравнение. Здесь мы предполагаем, что искомая величина найдена и оперируем ей как известной величиной. После нахождения х полученные результаты переводятся с математического языка на естественный.

Основные типы задач на проценты:Нахождение процентов от данного.Нахождение числа по его процентам.Нахождение процентного отношения.

Нахождение процента от числа Чтобы найти процент от числа, надо эточисло умножить на соответствующую дробь.Например: 20% от 45кг пшеницы равны 45·0,2=9 кг.

Нахождение числа по его проценту Чтобы найти число по его проценту, надочасть, соответствующую этому процентуразделить на дробь. Например: Если 8% от длины бруска составляют 2,4см, то длина всего бруска равна 2,4:0,08=30см

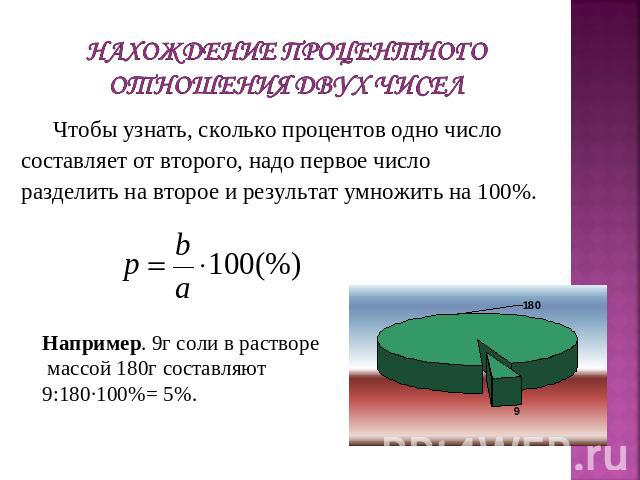
Нахождение процентного отношения двух чисел Чтобы узнать, сколько процентов одно числосоставляет от второго, надо первое числоразделить на второе и результат умножить на 100%. Например. 9г соли в растворе массой 180г составляют9:180·100%= 5%.

Формула расчета простых процентов Sp = [P * I * t : K] : 100I - годовая процентная ставкаt - количество дней начисления процентов по привлеченному вкладуK - количество дней в календарном году(365 или 366)P - сумма привлеченных в депозит денежных средствSp - сумма процентов (доходов)

Видоизмененная формула простых процентов S = P + [P * I * t : K] : 100S - сумма банковского вклада (депозита) с процентами,I - годовая процентная ставкаt - количество дней начисления процентов по привлеченному вкладуK - количество дней в календарном году(365 или 366)P - сумма привлеченных в депозит денежных средствПример: Предположим что банком принят депозит в сумме 50тыс. рублей сроком на 3 месяца по ставке 10,5 процентов «годовых»Sp = 50 000 * 10,5 * 90 : 365 : 100 = 1294,52S = 50 000 + 50 000 * 10,5 * 30 : 365 : 100 = 51 294,52

Формула расчета сложных процентов Sp = P * [(1 + I * t : K :100) n - 1]илиSp = S - P = P * (1 + I * t : K : 100) n – PI - годовая процентная ставкаt - количество дней начисления процентов по привлеченному вкладуK - количество дней в календарном году (365 или 366)P - сумма привлеченных в депозит денежных средствSp - сумма процентов (доходов).n - число периодов начисления процентов.S - сумма вклада (депозита) с процентами Однако, при расчете процентов проще сначала вычислить общуюсумму вклада с процентами, и только затем вычислять суммупроцентов (доходов). Формула расчета вклада с процентами будетвыглядеть так:S = P * (1 + I * t : K : 100) n

Формула расчета сложных процентов Пример: Принят депозит в сумме 50тыс. Рублейсроком на 90 дней по ставке 10,5 процентовгодовых с начислением процентов каждые 30 дней.S = 50 000 * (1 + 10,5 * 30 : 365 :100)3 ==51 305,72Sp = 50 000 * [(1 + 10,5 * 30 : 365 : 100)3 -1] = =1 305,72

Исследовательская часть Сфера применения процентов :в финансовой и экономической (банки), социальной (распределение населения),политической (голосование), коммунальной (повышение и понижение стоимости электроэнергии и квартплаты), в товарных отраслях ,в научной (химия, физика – величина КПД)

Проценты в банковской сфере: Задача 1. Вкладчик положил некоторую сумму на вклад «Новогодний» в Сбербанк России. Через три года вклад достиг 66550 рублей. Каков был первоначальный вклад при 11% годовых?Решение: Используем формулу сложного процента и находима (1+0,1)3 = 665501,331а = 66550а = 50000 (руб.) – первоначальный вклад Ответ: 50000 рублей первоначальный вклад при 11% годовых.

Проценты в торговле: Задача 2. Цена бананов в магазине«Копейка» первоначальносоставляла 21р.99коп. Сдекабря месяца цена сначалаподнялась на 15%, потом понизилась на 6,5%, затем снова поднялась на 10%.Какова цена бананов?Решение: По формуле сложного процента находим:21,99(1+0,15)(1,065)(1+0,1)=26(р)Ответ: 26 рублей цена бананов.

Проценты в политике: Задача 3.На выборах президента РФ вмарте приняли участие 68%избирателейПрилузского района. 50%от числа принявших участие ввыборах отдали голоса за избранногопрезидента Медведева Д.А. Сколькожителей проголосовало за него, еслив городе проживает 75 тыс. взрослогонаселения?Решение: Определим число избирателей, принявших участие в выборах:75000 · 68100 / 100 = 51000 (чел.)Определим число избирателей, отдавших голос за Медведева Д.А.:51000 · 50100 / 100 = 25500 (чел.)Ответ: 25500 человек проголосовало за Медведева.

Проценты в химии: Задача 4.Из 40 т руды выплавили 20 т металла, содержащего 6% примесей. Сколько процентов примесей в руде?Решение: В 20 т металла содержится 100 – 6 = 94%, или 20 ∙ 0,94= 18,8 (т) чистого металла, который составляет от массы руды 18,8 ∙100 / 40 = 47 %.Ответ: в руде 47 % примесей.

Заключение: Умение выполнять процентные вычисления и расчеты необходимо каждому человеку, так как с процентами мы сталкиваемся в повседневной жизни постоянно. Поэтому выбранная нами тема актуальна.В работе мы обобщили предыдущий опыт, связанный с темой «Проценты»,а также рассмотрелиболее сложные задачи по данной теме. Также мы узнали, что при решении задач на процентыможно использовать формулу сложного процента, а также схемы.

Заключение: Решенные нами задачи показали, что применение формулы «сложных процентов» весьма эффективна, поэтому нам бы хотелось, чтобы и остальные учащиеся нашего класса познакомились с ней и увидели ее эффективность, при решении более сложных задач по теме «Проценты».

Список используемой литературы: Алимов Ш.А., Алгебра: учеб. для 7 кл. общеобразоват. учреждений / Ш.А. Алимов, Ю.М. Колягин, Ю.В. Сидоров и др. - 10-е изд. – М.: Просвещение, 2002. – 207 с.: ил.Григорьева Т.П., Кузнецова Л.И., Перевощикова Е.Н., Пыжьянова А.Н. Пособие по элементарной математике: методы решения задач. Часть 2. 4 – е изд. – Н.Новгород: НГПУ, 2004. - 101 с.Иванова Т.А., Теоретические основы обучения математике в средней школе: Учебное пособие / Т.А. Иванова, Е.Н. Перевощикова, Т.П. Григорьева, Л.И. Кузнецова; Под ред. проф. Т.А. Ивановой. – Н.Новгород: НГПУ, 2003. – 320 с.Теляковский С.А., Алгебра 7 кл.: Учеб. для общеобразоват. учреждений. – 9-е изд. – М.: Просвещение, 2002. – 375 с.: ил.Шевкин А. В. , Материалы курса «Текстовые задачи в школьном курсе математики»: Лекции 1 – 8. – М.: Педагогический университет «Первое сентября», 2006. 80 с.