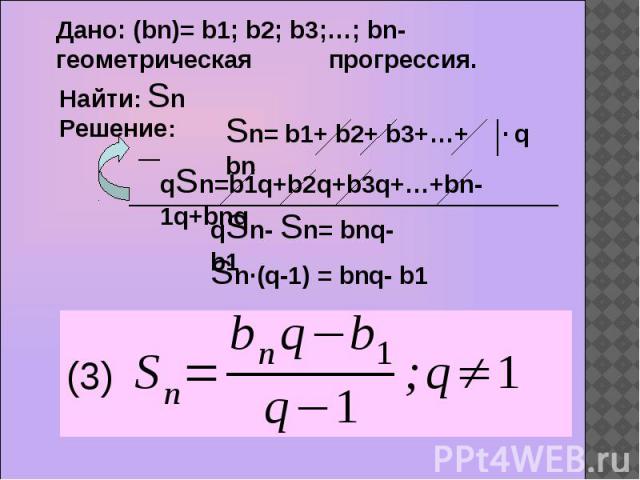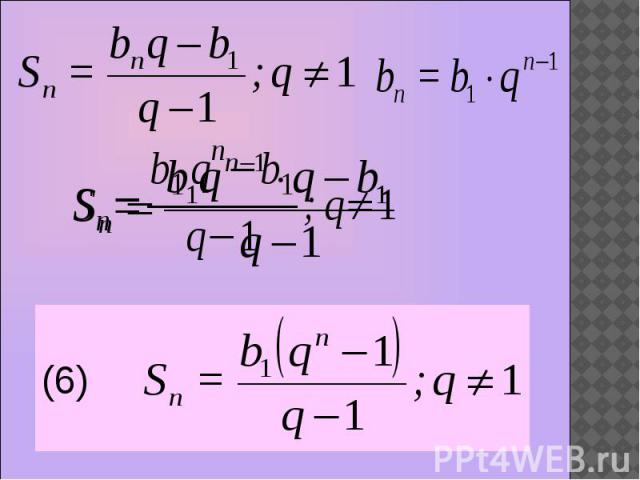Презентация на тему: Формулы для решения задач на прогрессии

Формулы для решения задач на прогрессииУрок алгебры в 9а классе28 февраля 2012г.

Вопрос 1: Какая из следующих последовательностей является арифметической прогрессией?А. Последовательность натуральных степеней числа 3.Б. Последовательность натуральных чисел, кратных 7.В. Последовательность квадратов натуральных чисел.Г. Последовательность чисел, обратных натуральным.

1. Какая из следующих последовательностей является арифметической прогрессией?

1. Какая из следующих последовательностей является арифметической прогрессией?Не верно.В этой последовательности разница между соседними числами изменяется, а должна быть постоянна.

Вопрос 2: Какая из следующих последовательностей не является геометрической прогрессией?А. Последовательность натуральных степеней числа 3.Б. Последовательность, все члены которой равны одному и тому же числу 3. В. Последовательность, состоящая из чередования чисел 3 и -3.Г. Последовательность, первый член которой равен 3, а все остальные члены - нули.

2. Какая из следующих последовательностей не является геометрической прогрессией?

2. Какая из следующих последовательностей не является геометрической прогрессией?Не верно.В этой последовательности отношение последующего члена к предыдущему равно одному и тому же не равному нулю числу, а значит, - это геометрическая прогрессия.

Вопрос 3: Какое число не является членом арифметической прогрессии 6, 12, 18, …?

3. Какое число не является членом арифметической прогрессии 6, 12, 18, …?

3. Какое число не является членом арифметической прогрессии 6, 12,18, …?Не верно.Вспомни, что аn = a1 + d(n-1), где a1 = 6, d = 12 – 6 = 6, откуда аn = 6 + 6(n-1) = 6 + 6n – 6 = 6n, то есть каждый из членов прогрессии нацело делится на число 6.

Вопрос 4: Какое число является членом геометрической прогрессии 6, 12, 24, …?

4. Какое число является членом геометрической прогрессии 6, 12, 24, …?

4. Какое число является членом геометрической прогрессии 6, 12, 24, …?Не верно.Вспомни, что q = bn+1 : bn , найди q = 12 : 6 = 2 и выпиши еще несколько членов данной прогрессии!

Вопрос 5: известны несколько последовательных Членов арифметической прогрессии: …-12; x; 14; 27… Найдите число x.А. -1Б. 0В. 1Г. 2

Не верно!Определи разность прогрессии или вспомни ее характеристическое свойство!Определи разность прогрессии или вспомни ее характеристическое свойство!

5. известны несколько последовательных Членов арифметической прогрессии: …-12; x; 14; 27… Найдите число x.

Вопрос 6: известны несколько последовательных членов геометрической прогрессии: Вопрос 6: известны несколько последовательных членов геометрической прогрессии: …2; y; 8; -16;… Найдите число Y.А. – 4 Б. – 5 В. 4 Г. 5

6. известны несколько последовательных членов геометрической прогрессии: …2; y; 8; -16;… Найдите число Y.Определи знаменатель прогрессии или вспомни ее характеристическое свойство!

6. известны несколько последовательных членов геометрической прогрессии: …2; y; 8; -16;… Найдите число Y.

Вопрос 7: Найди сумму первых пяти членов геометрической прогрессии, если известно, что ее первый член равен 48, а знаменатель равен -0,5. Вопрос 7: Найди сумму первых пяти членов геометрической прогрессии, если известно, что ее первый член равен 48, а знаменатель равен -0,5. А. – 93 Б. – 33 В. 33 Г. 93

7. Найди сумму первых пяти членов геометрической прогрессии, если известно, что ее первый член равен 3, а знаменатель равен -2. Выпиши первые четыре члена прогрессии и сложи их!

7. Найди сумму первых пяти членов геометрической прогрессии, если известно, что ее первый член равен 3, а знаменатель равен -2.

Вопрос 8: Найди сумму первых восьми членов арифметической прогрессии, если известно, что ее первый член равен 4, а разность равна -2.А. – 18Б. – 20В. – 24Г. – 32

8. Найди сумму первых восьми членов арифметической прогрессии, если известно, что ее первый член равен -4, а разность равна 2.Выпиши первые восемь членов прогрессии, а затем сложи их.

Молодец! Правильно!!!8. Найди сумму первых восьми членов арифметической прогрессии, если известно, что ее первый член равен -4, а разность равна 2.

Задача гаусса

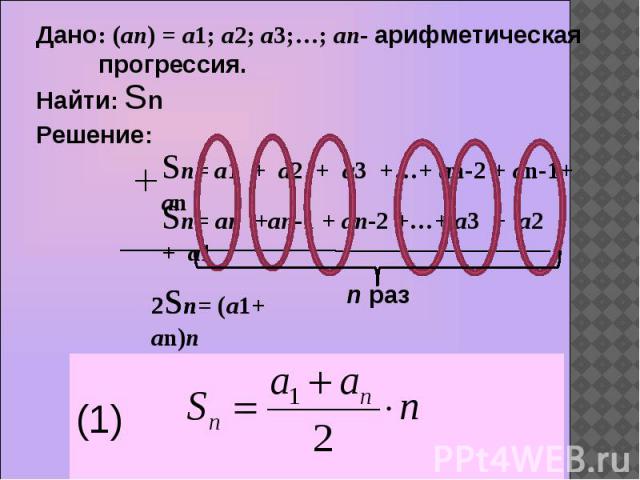
Дано: (an) = a1; a2; a3;…; an- арифметическая прогрессия.

Формула суммы членов конечной арифметической прогрессии

Практическое применение формулы суммы первых n первых членов арифметической прогрессии(an) – арифм. прогрессия a1 = 1, d=1, n = 100 S100 = ?

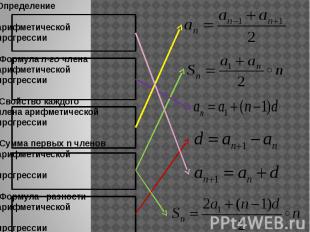
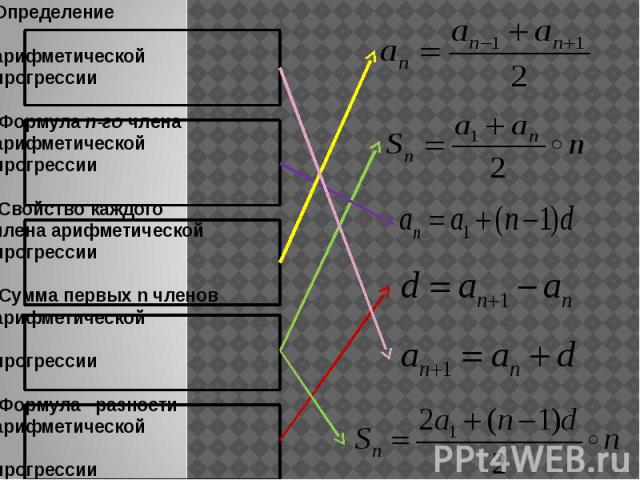
Определение арифметическойпрогрессии Формула n-го членаарифметическойпрогрессии Свойство каждогочлена арифметическойпрогрессии Сумма первых n членоварифметической прогрессии Формула разностиарифметической прогрессии

Задача о сметливом крестьянине и глупом купце

2S30=2 + 4 + 8 +16 +32+...+229 +230

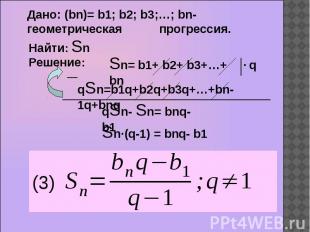
Дано: (bn)= b1; b2; b3;…; bn- геометрическая прогрессия.

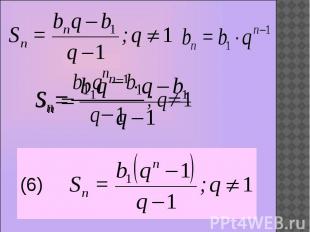
Практическое применение формулы суммы первых n первых членов геометрической прогрессии(bn) – геом. прогрессия b1 = 1, q=2, n = 30 S30 = ?

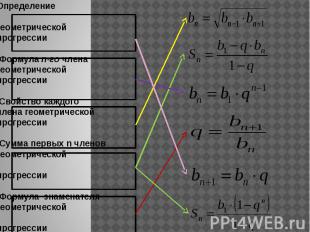
Определение геометрическойпрогрессии Формула n-го членагеометрическойпрогрессии Свойство каждогочлена геометрическойпрогрессии Сумма первых n членовгеометрической прогрессии Формула знаменателягеометрической прогрессии

Домашнее задание1) читать п.п. 26 и 28 учебника;2) выполнить творческую работу «Шпаргалка с формулами для решения задач на прогрессии»;3) записать в тетради доказательство всех выведенных на уроке формул.

Результатом своей личной работы считаю, что я … А. Разобрался в теории. Б. Научился решать задачи В. Повторил весь ранее изученный материал. Г. Не узнал ничего нового.Чего мне не хватало на уроке при решении задач? А. Знаний. Б. Времени. В. Желания. Г. Решал нормально.Кто оказал мне наиболее существенную помощь в преодолении трудностей на уроке? А. Одноклассники. Б. Учитель. В. Слайды презентации. Г. Никто.