Презентация на тему: Алгоритм решения неравенств

Решение неравенств 5klass.net

Для любых двух простейших чисел а и в выполняется одно из двух условий: либо а больше в (а>в), либо а меньше в (а

Неравенства делятся на строгие и нестрогие Строгое неравенство А(х) > В(х) А(х) < В(х) А(х) ≥ В(х) Строгое неравенство Не строгое неравенство Не строгое неравенство А(х) ≤ В(х)

Решим простейшее линейное неравенство ? 5х + 3 > 3х+7 Сначала вычтем из обеих частей 3х + 3: 2х > 4 Этот перевод опирается на одно из важнейших свойств числовых неравенств: Для любых действительных чисел а, в и с если а > в, то а + в > в + с.

Если х0 – решение данного неравенства, то, добавляя к обоим частям число с = - (3х0 + 3), получим, что х0 удовлетворяет и неравенству 2х0 > 4. Верно и обратное. Пользуясь другим свойством неравенств, разделим обе части на2. Получим х > 2. Всё множество решений представляется числовым лучом (2; ∞). если а > в и с> 0, то ас > вс,

Теперь решим квадратное неравенство ах2 + bх + с > 0, где а ≠ 0.

? ! ? !

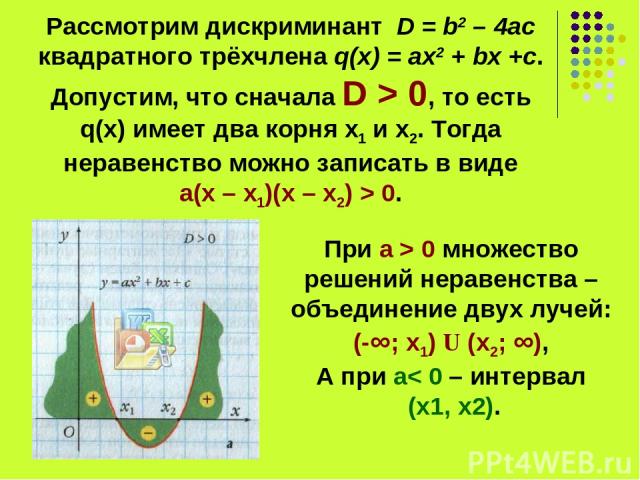
Рассмотрим дискриминант D = b2 – 4ac квадратного трёхчлена q(x) = aх2 + bx +c. Допустим, что сначала D > 0, то есть q(x) имеет два корня х1 и х2. Тогда неравенство можно записать в виде а(х – х1)(х – х2) > 0. При а > 0 множество решений неравенства – объединение двух лучей: (-∞; х1) U (х2; ∞), А при а< 0 – интервал (х1, х2).

Случай D = 0, когда х1 = х2 и q(x) = a(x –x1)2, рассматривается аналогично

Если же D < 0, то функция q(x) имеет один и тот же знак на всей действительной прямой. То есть функция q(x) положительна при а> 0 и отрицательна при а < 0.

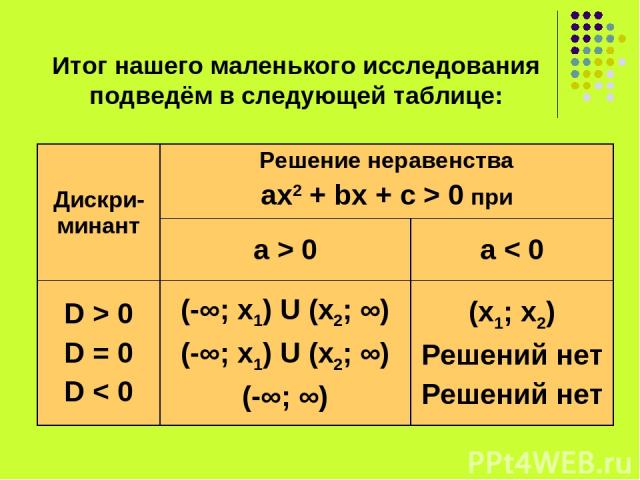
Итог нашего маленького исследования подведём в следующей таблице: Дискри-минант Решение неравенства ах2 + bx + c > 0 при a > 0 a < 0 D > 0 D = 0 D < 0 (-∞; х1) U (х2; ∞) (-∞; х1) U (х2; ∞) (-∞; ∞) (х1; х2) Решений нет Решений нет

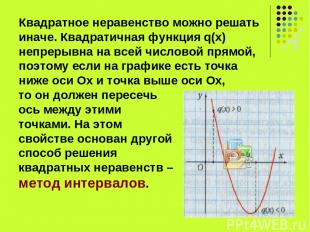
Квадратное неравенство можно решать иначе. Квадратичная функция q(x) непрерывна на всей числовой прямой, поэтому если на графике есть точка ниже оси Ох и точка выше оси Ох, то он должен пересечь ось между этими точками. На этом свойстве основан другой способ решения квадратных неравенств – метод интервалов.

Алгоритм решения неравенств методом интервалов (квадратных и не только): Найдём нули функции (абсциссы точек пересечения графика данной функции с осью Ох). 2. Отметить нули функции на координатной прямой пустыми (если неравенство строгое) или сплошными (если неравенство не строгое) точками. 3. Определить знак функции на каждом промежутке (а для квадратичной функции достаточно определить знак лишь в одном из промежутков, так как знаки будут чередоваться потому, что функция непрерывна на всей области определения). 4. а) Выделить те промежутки, где q(x) > 0. б) Выделить те промежутки, где q(x) < 0.

Пример: решим неравенство методом интервалов. 1. Нули функции 2/3; 2. Область определения: х ≠ -4; 3. Ответ: (-∞; -4) U [2/3; ∞)

Егорова Татьяна Давыдова Екатерина Над роликом работали: ученицы 9 В класса МОУ «СОШ № 17» г. Прокопьевска