Презентация на тему: Разработка методических рекомендаций обучения решению заданий с развернутым ответом, критерии оценки заданий по решению геометрических задач типа С

«Разработка методических рекомендаций обучения решению заданий с развернутым ответом, критерии оценки заданий по решению геометрических задач типа С »

Выбор темы обусловлен необходимостью развития у старшеклассников геометрического воображения, логического, критического и абстрактного мышления, способности к анализу, исследованию задач курса планиметрии, поиску их верного решения.

Актуальность выбора данной темы состоит в том, что повышение качества знаний и умений учащихся по решению задач планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;окружность, свойства касательных, хорд, вписанных и описанных углов;площади фигур;свойства медианы, высоты, биссектрисы и других теоретических аспектов геометрических знаний, способствует повторению всего курса математики 5-11 классов:

Актуальность выбора данной темы состоит в том, что повышение качества знаний и умений учащихся по решению задач планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;окружность, свойства касательных, хорд, вписанных и описанных углов;площади фигур;свойства медианы, высоты, биссектрисы и других теоретических аспектов геометрических знаний, способствует повторению всего курса математики 5-11 классов:

Актуальность выбора данной темы состоит в том, что повышение качества знаний и умений учащихся по решению задач планиметрического типа, предполагающее обеспечение теоретической базы по материалу:свойства треугольников, параллелограмма, многоугольников;окружность, свойства касательных, хорд, вписанных и описанных углов;площади фигур;свойства медианы, высоты, биссектрисы и других теоретических аспектов геометрических знаний

способствует повторению всего курса математики 5-11 классов:вычислений, формул сокращенного умножения, решения квадратных уравнений;решения рациональных, иррациональных, тригонометрических уравнений и их систем;использование свойств степени с рациональным показателем; использование свойств тригонометрических функций.

Основной проблемой для учащихся при решении планиметрических задач является: во-первых, недостаточное геометрическое воображение, позволяющее «видеть» задачу , выделить основные аспекты геометрии, на которые необходимо ссылаться при ссылке на теоретические сведения; во – вторых, недостаточная теоретическая база знаний из курса геометрии 7-9 классов ,позволяющая найти необходимое и достаточное для поиска верного решения задачи. Кроме того, именно в планиметрических задачах типа С ученик может потерять баллы из-за недостаточно полного пояснения хода решения.

Для повышения качества навыков учащихся в отношении решения планиметрических задач типа С, необходимо при их подготовке к ЕГЭ обеспечить достаточную теоретическую базу знаний, развивать геометрическое воображение через рассмотрение разных случаев и разных способов решения задач. Для этого учителю необходимо развивать у учеников способности к анализу и синтезу; систематизировать имеющиеся у них знания о представлениях и различных свойствах плоских фигурах.

Подготовка учащихся к решению планиметрических задач типа С с развернутым ответом на ЕГЭ по математике, прежде всего, предполагает:основательное обеспечение теоретической базы знаний курса геометрии 7- 9 класса;развитие геометрического воображения, логики, критического и абстрактного мышления,формирование практических навыков решения задач повышенной сложности об углах, окружностях, многоугольниках, взаимном расположении геометрических фигур на плоскости.

Решение на ЕГЭ планиметрических задач типа С4 включает такие параметры как: верно изображенный чертеж, с учетом всех случаев, если возможных решений предусмотрено более одного, позволяющий ученику «увидеть» задачу и быстро определить ход её решения;четкое обоснование решения со ссылкой на теоретические сведения – аксиомы, леммы, теоремы и следствия из них, определяющие свойства планиметрических фигур и их взаимного расположения;развернутый точный ответ на конкретно поставленный вопрос задачи.

Критерии оценивания выполнения задания С4 3 балла: рассмотрены все возможные геометрические конфигурации и обоснованно получен правильный ответ.2 балла:рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой обоснованно получено правильное значение искомой величины.1 балл: рассмотрена хотя бы одна возможная геометрическая конфигурация, в которой получено значение искомой величины, неверное из-за арифметической ошибки.0 баллов: решение не соответствует ни одному из критериев, перечисленных выше.

Для обеспечения качества решения планиметрических задач учителю нужно при повторении материала систематизировать теоретические сведения по направлениям: ТреугольникиПрямоугольный треугольник: теорема Пифагора; связь высоты к гипотенузе треугольника и его катетов с проекциями катетов на гипотенузу; свойство медианы, проведенной к гипотенузе; подобие прямоугольных треугольников; определение синуса, косинуса и тангенса углов.Равносторонний и равнобедренный треугольник: свойства медианы; углов; Сумма углов треугольника; внешний угол; равенство и подобие треугольников; теорема синусов и следствие из неё; теорема косинусов; свойство биссектрисы; вписанные и описанные окружности; взаимосвязь радиусов вписанной и описанной окружностей с площадью треугольника; средняя линия треугольника;

Параллелограмм: определение, свойства сторон, углов и диагоналей; определения и свойства ромба, прямоугольника, квадрата; периметр и площадь; Трапеция: определение, свойства, определения и свойства равнобедренной, прямоугольной трапеций; свойство средней линии, периметр и площадь; трапеция, вписанная в окружность или описанная вокруг неё;Четырехугольники: вписанные в окружность и описанные;Правильные многоугольники: радиусы вписанных и описанных окружностей ; площади и периметр; внутренние и внешние углы;Окружность: свойства касательных, хорд, секущих; вписанные и центральные углы; длина и мера дуги; длина окружности и площадь круга; сектор и сегмент.

Для формирования навыков полного обоснования решения не диктовать ход решения, не подсказывать его, а побуждать к самостоятельному анализу условия задачи, планированию хода решения;в форме эвристической беседы с учащимися формировать способность к предвидению верного хода решения: для этого – подбирать необходимые и достаточно ёмкие вопросы, способствующие самостоятельному поиску нужного хода решения учащимися;через систематическое повторение добиться максимального запоминания учащимися теоретических сведений через понимание, а не зазубривание;во время решения каждой задачи развивать способность к полному, но, в то же время, четкому и грамотному изложению математической мысли, без лишних слов и посторонних теоретических выкладок;при решении задач обращать внимание на аккуратность и четкость выполнения рисунка к задаче, выделение в нем известных данных и требуемых для нахождения, дополнительные построения.

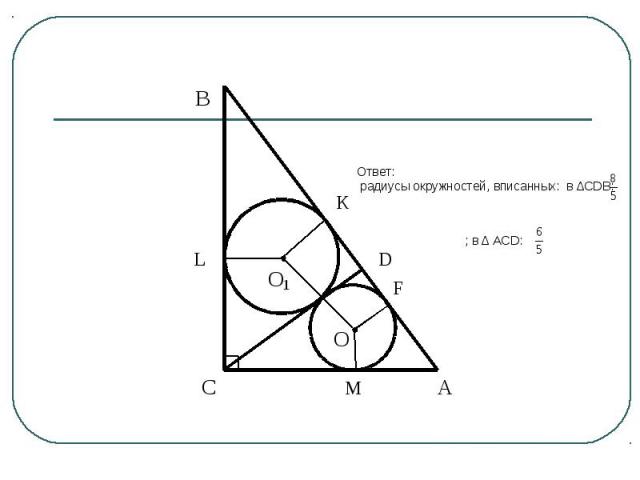
Задача 1 В прямоугольном треугольнике катеты равны 6 и 8. Из вершины прямого угла проведена высота CD. Определите радиусы вписанных окружностей в треугольники ACD и CDB.

План решения Составить с учениками необходимый чертеж;Проанализировать условие задачи: для этого задать соответствующие вопросы:- что означает – вписанные окружности в треугольники ACD и CDB?;- определение и свойства касательных к окружности?;- свойство перпендикуляров к одной прямой?- что можно сказать о треугольниках, образованных высотой, проведенной к гипотенузе прямоугольного треугольника?;- как связаны проекции катетов на гипотенузу, катеты и высота к гипотенузе прямоугольного треугольника из подобия треугольников?;- какая формула радиуса вписанной в треугольник окружности получена из свойств касательных к окружности? ;- сколько существует случаев для схематического изображения рисунка в данной задаче?;- каких данных достаточно и что необходимо найти для поиска ответа?Сформулировать и обосновать решение задачи, найти верный ответ.Проанализировать: за что могут быть сняты баллы на ЕГЭ в задаче такого типа.

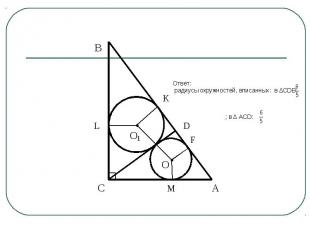
Ответ: радиусы окружностей, вписанных: в ∆CDB:

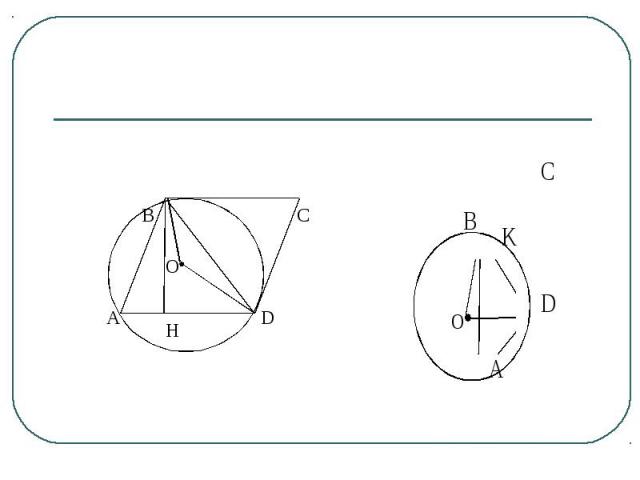
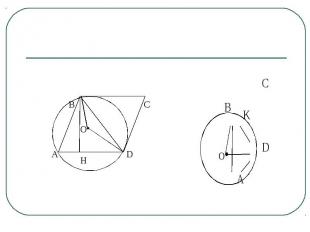
Задача 2 В параллелограмме ABCD острый угол при вершине А равен 300, сторона CD касается окружности радиуса 6, описанной около треугольника ABD . Определите площадь параллелограмма.

План решения задачи:Рассмотреть разные случаи, выполнив рисунки (рис.2, рис. 3);Проанализировать условие задачи, обозначив наводящие вопросы:- определение и свойства параллелограмма?;- теорема о вписанных в окружность углах?;- определение окружности, описанной вокруг треугольника?;- сколько существует случаев решения данной задачи?;- формулы для нахождения площади параллелограмма?;- каких данных достаточно и что необходимо найти для поиска ответа?

Работая над составлением собственного алгоритма решения определенной задачи, ученики постепенно приучаются совершать подобную деятельность автоматически, знания и умения переходят в навыки решения планиметрических задач. Обоснование решения задач соответствует основным требованиям, касающимся уровню и характеру объяснения решения задач.