Презентация на тему: Задачи по комбинаторике

Задачи по комбинаторике выполнила ученица 5а класса Пятакова Дарья

Введение Человеку часто приходится иметь дело с задачами, в которых нужно подсчитать число всех возможных способов расположения некоторых предметов или число всех возможных способов осуществления некоторого действия. Разные пути или варианты, которые приходится выбирать человеку, складываются в самые разнообразные комбинации.

Актуальность и значимость Комбинаторные задачи развивают нестандартное мышление, воображение, смекалку. Задачи по комбинаторике включены на всех этапах математической олимпиады.

проблема цель задачи методы

Проблема Отсутствие возможности хорошо подготовиться к конкурсам и к олимпиаде. (Недостаток времени , беден задачный материал )

Цель работы: выяснить, что значит решить комбинаторную задачу, т.е. познакомиться с методами решения задач из комбинаторики.

Задачи исследования: Рассмотреть методы решения некоторых комбинаторных задач;Создать задачник по комбинаторике для 5-6 классов;Расширить знания по теме «Комбинаторные задачи»;Научиться собирать информацию, выделять главное, делать выводы.

Объект исследования:область математики – комбинаторика. Методы исследования:КлассификацияСистематизацияСравнение Анализ математической литературы

Результат Создание сборника задач

Задача: На столе лежат 3 черных и 5 красных карандашей. Сколькими способами можно выбрать карандаш любого цвета?Решение: Выбрать карандаш любого цвета можно 5+3=8 способами.

Задача: В классе 10 учащихся занимаются спортом, остальные 6 учащихся посещают танцевальный кружок. 1)Сколько пар учащихся можно выбрать так, чтобы один из пары был спортсменом, другой танцором? 2)Сколько возможностей выбора одного ученика?Решение:1)Возможность выбора спортсменов 10, а на каждого из 10 спортсменов выборов танцора 6. Значит, возможность выбора пар танцора и спортсмена 10·6=60. 2) Возможность выбора одного ученика 10+6=16.

Задача : Из города А в город В ведут 3 дороги. А из города В в город С ведут 4 дороги. Сколько путей, проходящих через В, ведут из А в С? Решение: Можно рассуждать таким образом: для каждой из трех путей из А в В имеется четыре способа выбора дороги из В в С. Всего различных путей из А в С равно произведению 3·4, т.е. 12

Задача: В школьной столовой имеются 2 первых, 5 вторых и 4 третьих блюд. Сколькими способами ученик может выбрать обед, состоящий из первых, вторых и третьих Решение: Первое блюдо можно выбрать 2 способами. Для каждого выбора первого блюда существует 5 вторых блюд. Первые два блюда можно выбрать 2·5=10 способами. И, наконец, для каждой 10 этих выборов имеются четыре возможности выбора третьего блюда, т. е. Существует 2·5·4 способов составления обеда из трех блюд. Итак, обед может быть составлен 40 способами.

Примеры задач Проказница Мартышка,Осёл,Козёл,Да косолапый КвартетМишкаЗатеяли играть в квартет…Стой, братцы стой! – Кричит Мартышка, - погодите!Как музыке идти?Ведь вы не так сидите…И так, и этак пересаживались – опять музыка на лад не идет.Вот пуще прежнего пошли у них разборыИ споры,Кому и как сидеть…

Решение Вероятно, крыловские музыканты так и не перепробовали всех возможных мест. Однако способов не так уж и много. Сколько?Решение: 4!=24 варианта перестановок.

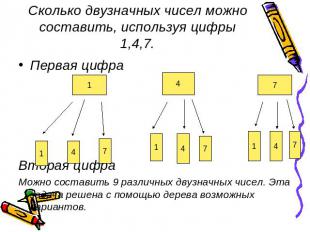
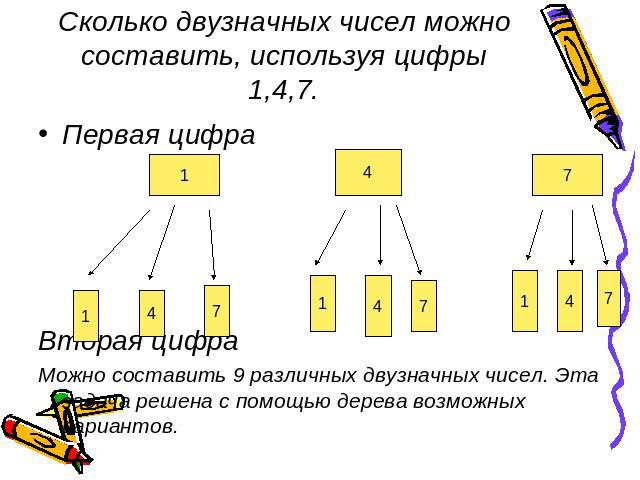
Сколько двузначных чисел можно составить, используя цифры 1,4,7. Первая цифраВторая цифраМожно составить 9 различных двузначных чисел. Эта задача решена с помощью дерева возможных вариантов.

Вывод: Научилась решать задачи по комбинаторике;Подобрала задачи по данной теме и создала задачник;Приобрела умения работать с компьютером.

Заключение Я считаю, что работа достигла своих целей.Создала сборник задач по комбинаторикеЭтот сборник заинтересует учащихся, поможет развитию их кругозора и мышления, будет способствовать более качественной подготовке к конкурсам и к олимпиадам. Может быть использована на уроках, кружках, индивидуальных занятиях .

Спасибо за внимание.