Презентация на тему: Тетраэдр, виды сечений и решение задач по тетраэдру

Министерство образованияРоссийской Федерации. М О У «Средняя общеобразовательная школа № 81» Научно – практическая работа по теме:«Тетраэдр, виды сечений и решение задач по тетраэдру» Выполнил: Патрушев АлександрУченик 11 «А» класса.Руководитель: Чеппе Инесса Валентиновна – учитель высшей квалификационной Категории. Новокузнецк 2009г.

Цель работы: Выяснить какие виды сечений тетраэдра существуютТерминологияПоказать на примерах решения задач тетраэдра

Терминология: Тетраэдр – поверхность, составленная из четырех треугольников Сечение – многоугольник, образованный при пересечении граней тетраэдра секущей плоскостью, сторонами которого являются отрезки по которым они пересекаются.

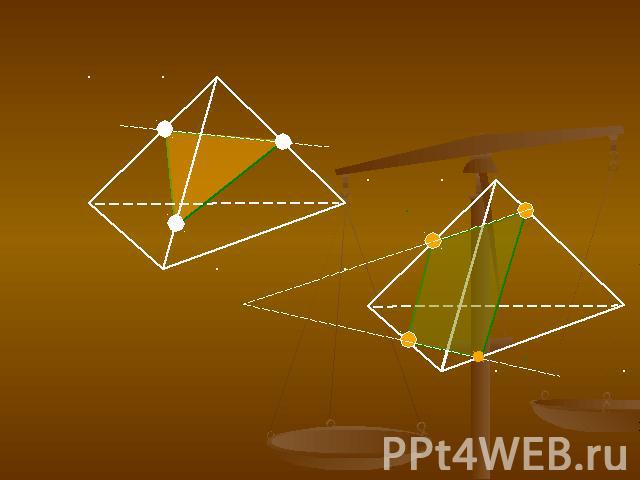
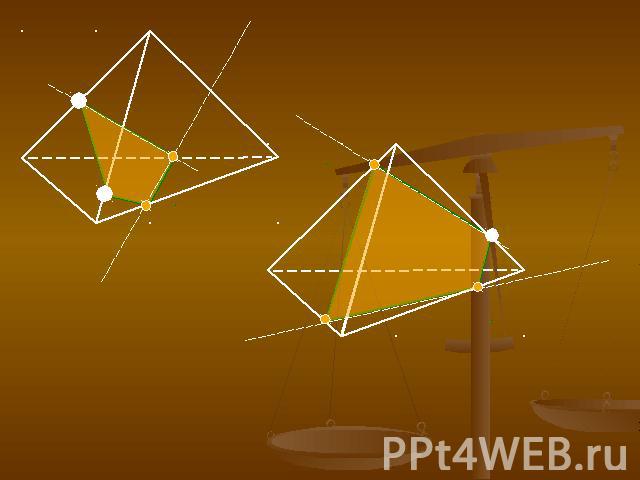
Виды сечений:

Геометрическое утверждение Если две точки одной прямой лежат в плоскости, то и вся прямая лежит в этой плоскости.

Задача №1 Назовите все пары скрещивающихся(т.е.принадлежащих скрещивающимся прямым) ребер тетраэдра ABCD. Сколько таких пар ребер имеет тетраэдр?

Решение: В тетраэдре три пары скрещивающихся ребер:AC и DB;AB и DC;AD и CB.

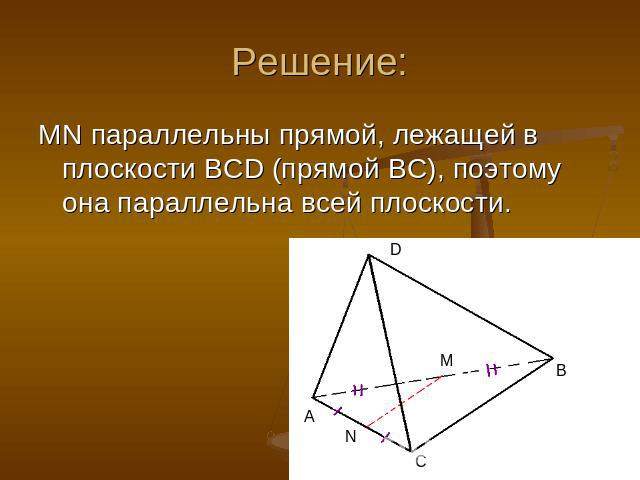
Задача №2 Точки М и N – середины ребер AB и BC тетраэдра ABCD. Докажите, что прямая MN параллельна плоскости BCD.

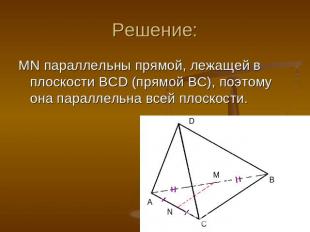
Решение: MN параллельны прямой, лежащей в плоскости BCD (прямой BC), поэтому она параллельна всей плоскости.

Задача №3 Через середины ребер AB и BC тетраэдра SABC проведена плоскость параллельно ребру SB. Докажите , что эта плоскость пересекает грани SAB и SBC по параллельным прямым.

Решение: Плоскость SBC и плоскость, проходящая через прямую MN параллельно ребру SB, пересекаются по прямой, проходящей через точку N.По теореме линия пересечения параллельна SB. В плоскости SBC через т.N проходит NQ SB.Плоскость SAB и плоскость MNQ пересекаются по прямой, проходящей через т. М(прямая MP).По теореме линия пересечения параллельна SB. PM SBNQ SB Утверждение доказано.

Заключение: В результате работы над темой я изучил терминологию , виды сечения. Рассмотрел задачи на построение сечений , предложенных в различных спецкурсах по геометрии.

Используемая литература: 1. Л.В. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Л.С. Киселева, Э.Г. ПознякГеометрия: учебник для 10-11 кл. общеобразовательных учреждений Базовый и профильный уровни