Презентация на тему: Точки максимума и минимума

Разработала учитель математики МБОУ «Красногвардейская школа №1» Коваленко Инна Николаевна

-5х + 1 > 0; х2 + 2х - 3 < 0; (х + 2)ех < 0.

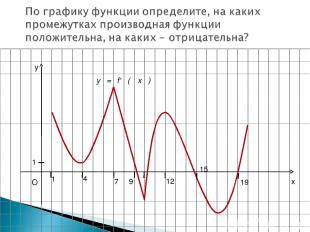
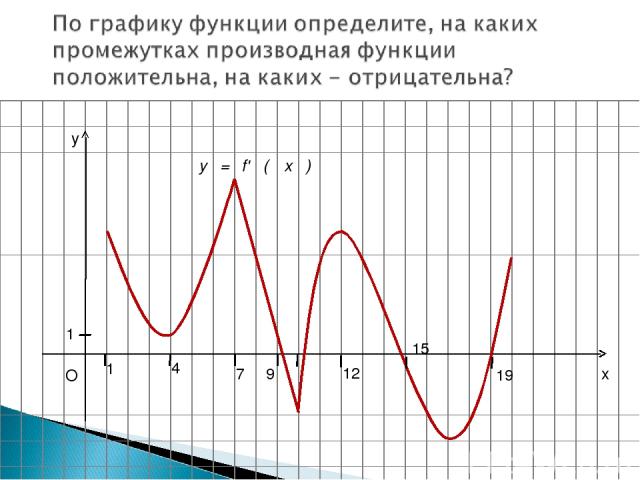
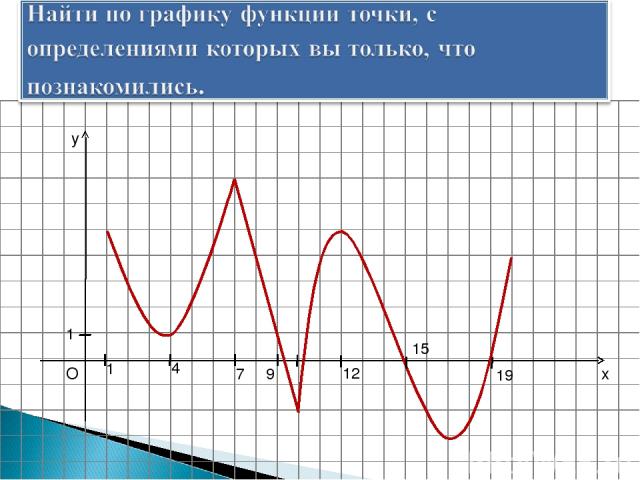
x y O 1 1 4 7 9 12 15 19 у = f' ( x )

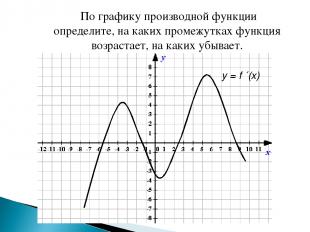
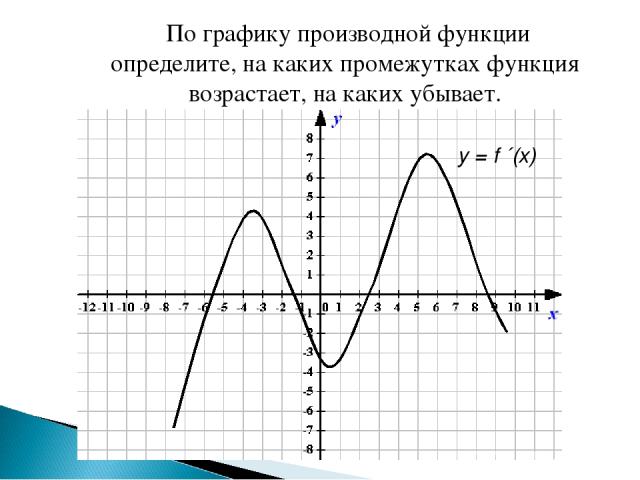
По графику производной функции определите, на каких промежутках функция возрастает, на каких убывает. y = f ´(х)

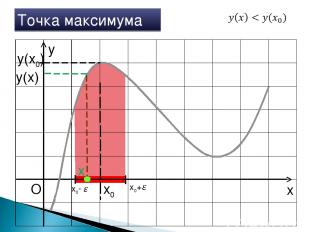
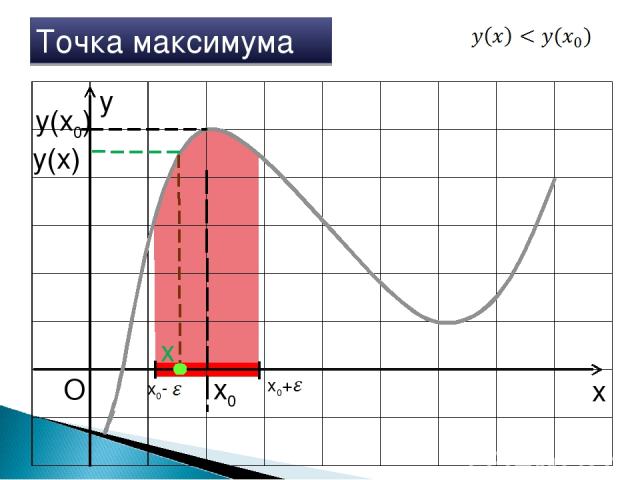
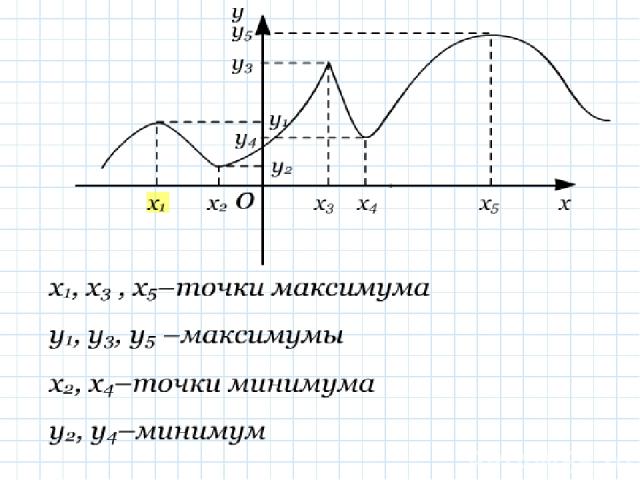
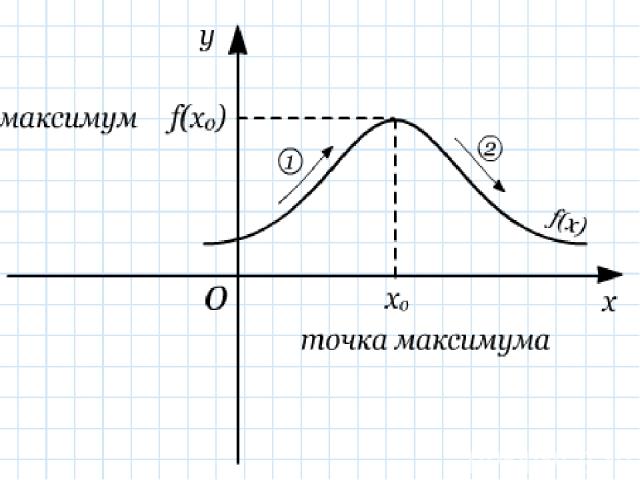
x y O x0 Точка максимума x0+ x0- x y(x0) y(x)

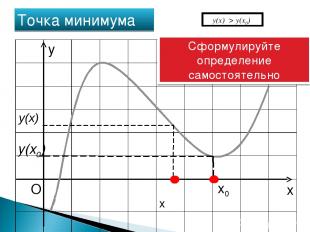
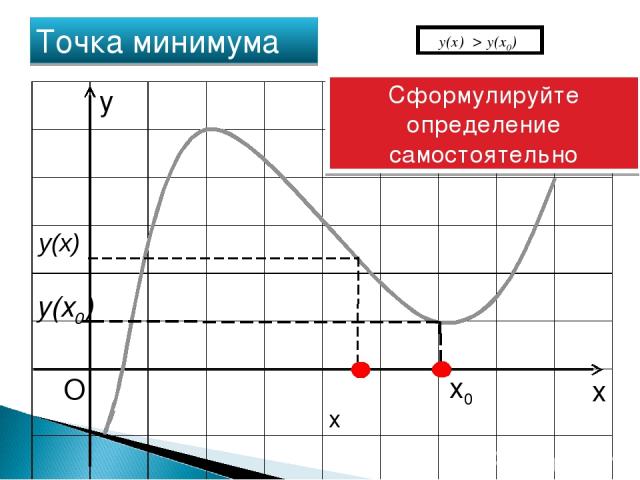
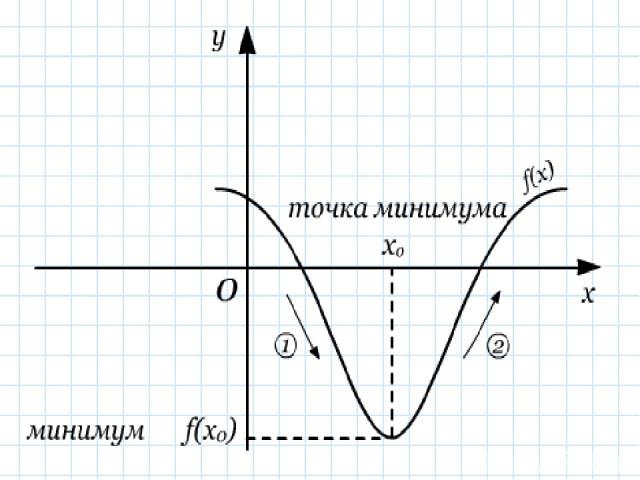
x O x0 Точка минимума y(x0) y Сформулируйте определение самостоятельно y(х) > y(x0) y(x) x

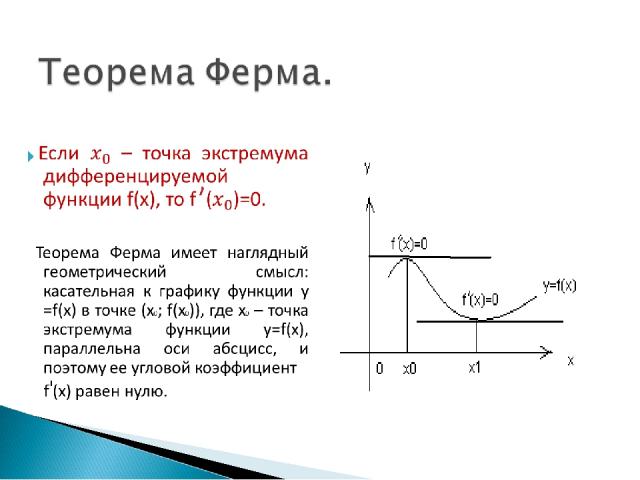
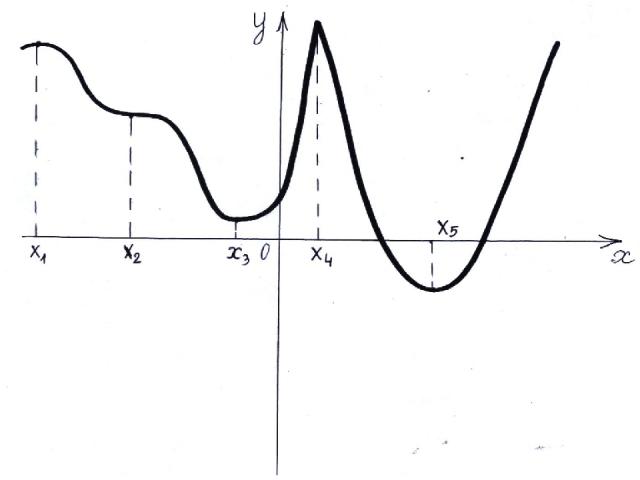
Точки максимума и минимума называются точками экстремума функции

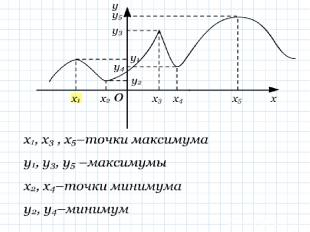
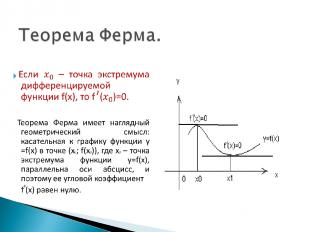
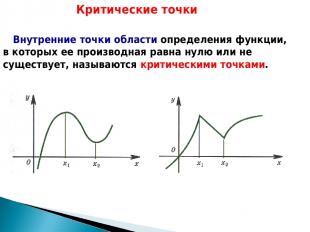
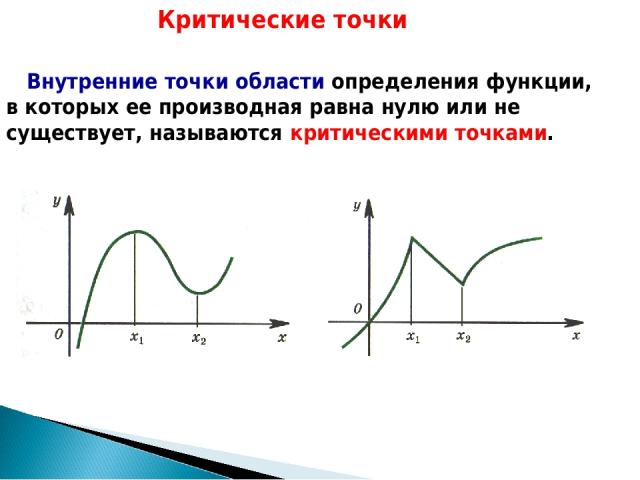
Внутренние точки области определения функции, в которых ее производная равна нулю или не существует, называются критическими точками. Критические точки

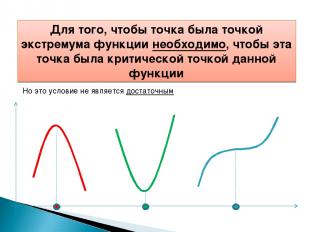
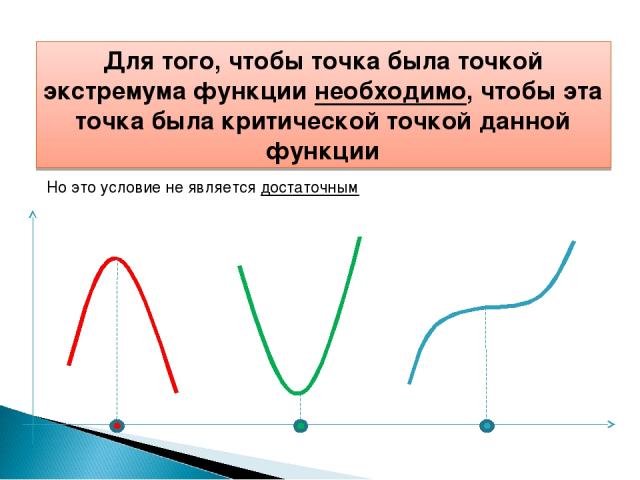
Для того, чтобы точка была точкой экстремума функции необходимо, чтобы эта точка была критической точкой данной функции Но это условие не является достаточным

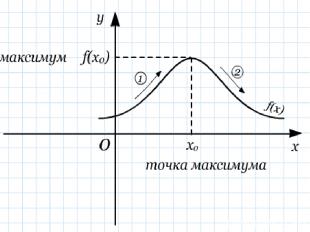
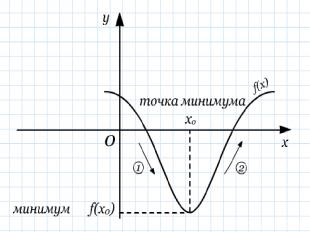
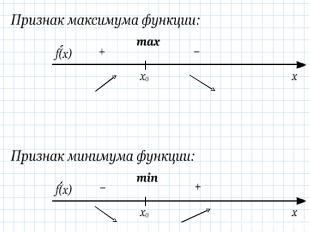
Для того , чтобы точка х0 была точкой экстремума функции f(х): необходимо , чтобы х0 была критической точкой функции; достаточно, чтобы при переходе через критическую точку х0 производная меняла знак.

Найти производную функции. Решить уравнение f ´(х)=0, и найти тем самым стационарные точки. Методом интервалов установить промежутки знакопостоянства производной. Если при переходе через точку х0: - производная не меняет знак, то х0 – точка перегиба; - производная меняет знак с «+» на «-», то х0 точка максимума; - производная меняет знак с «-» на «+», то х0 точка минимума.

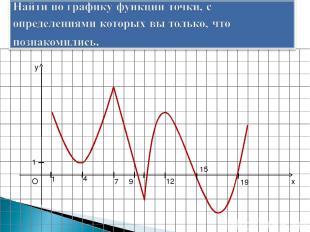
x y O 1 1 4 7 9 12 15 19

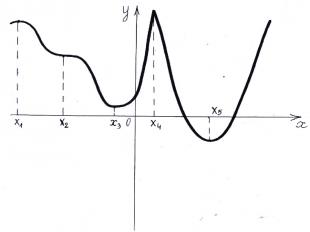
Решение: 1) Найдем производную функции: f ´ (x)=9 2) Найдем стационарные точки: Стационарных точек нет. 3) Данная функция линейная и возрастает на всей числовой оси, поэтому точек экстремума функция не имеет. Ответ: функция f(x)=9х-3 не имеет точек экстремума.

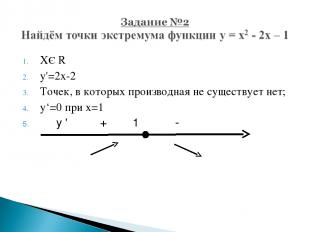
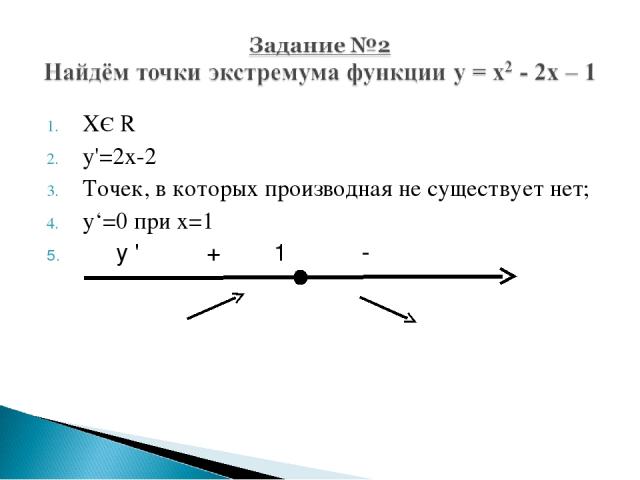
XЄ R y'=2x-2 Точек, в которых производная не существует нет; y‘=0 при х=1 у ' + 1 -

№ 5.6 (а) решение у доски № 5.7 (в)решение у доски с комментарием №5.10 (а) самостоятельно

1. п. 5.1, выучить определения и алгоритм нахождения точек экстремума., №5.8 (б,г), №5.6 (б,г) 2. Решение В8 (сборник ЕГЭ 3000 задач) №1685, №1743, №1752, №1942 - устно